Ken

3分で復習できる！中学3年生の数学のまとめ

中学3年生の数学を復習できるまとめ

QIKERUの記事を中学3年生の数学の単元ごとにまとめてみたよ。

テストや試験の復習に参考にしてね！

 

中学数学　復習　まとめ

 

Chapter1. 式の展開と因数分解

二次方程式を解くために必要な計算方法を勉強していくよ。

 

式の展開とは？

 

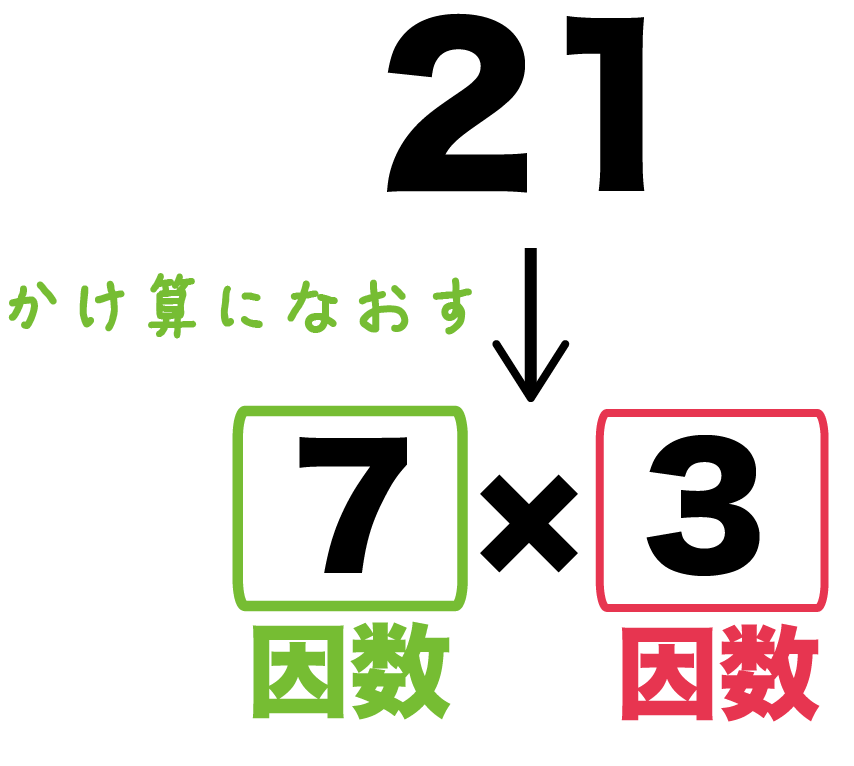
素因数分解とは何か？

 

因数分解とは何か？

 

 

Chapter2. 平方根・ルート計算

二次方程式や三平方の定理で活躍する「平方根の計算方法」を勉強していくよ。

 

平方根・根号とは何か？

 

有理数と無理数とは？

 

ルート・平方根の計算方法

 

 

Chapter3. 二次方程式

いよいよ二次方程式を解いていくよ。

 

二次方程式とはなんだろう？？

 

二次方程式の解き方

 

解の公式

 

二次方程式の文章問題の解き方

 

 

Chapter4. 「2乗に比例する関数y=ax²」

二次方程式を使って次数が2の関数を勉強していこう。

 

2乗に比例する関数とは？？

 

二次関数y=ax²のグラフ

 

関数y=ax²の文章問題

 

 

 Chapter5. 相似な図形

相似な図形にチャレンジ！

 

相似の基本

 

相似の証明

 

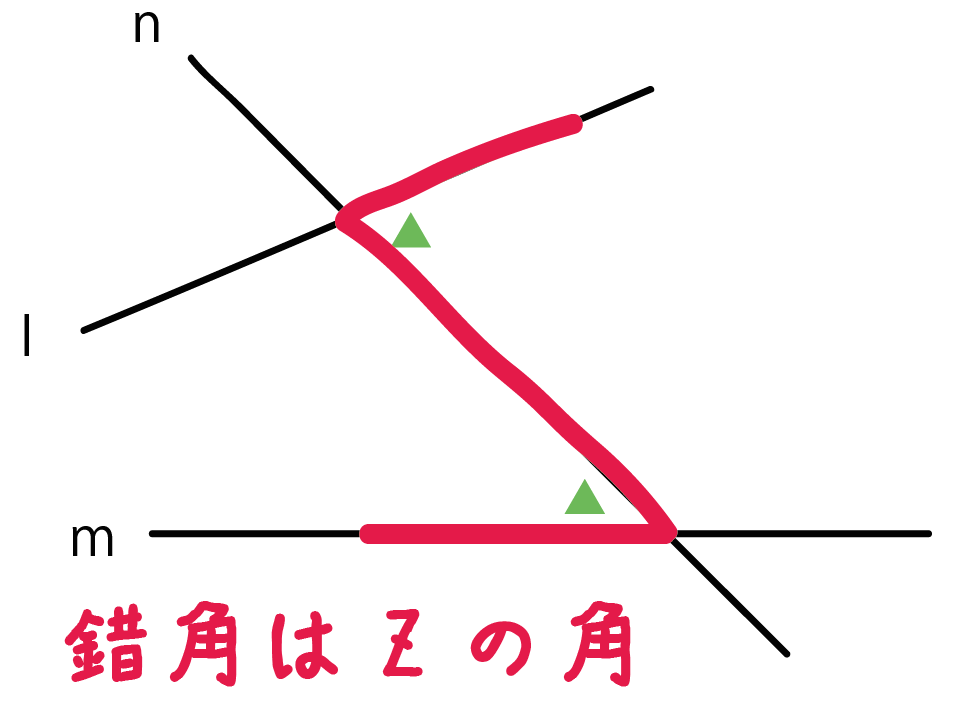
平行線と線分の比

 

中点連結定理とは？？

 

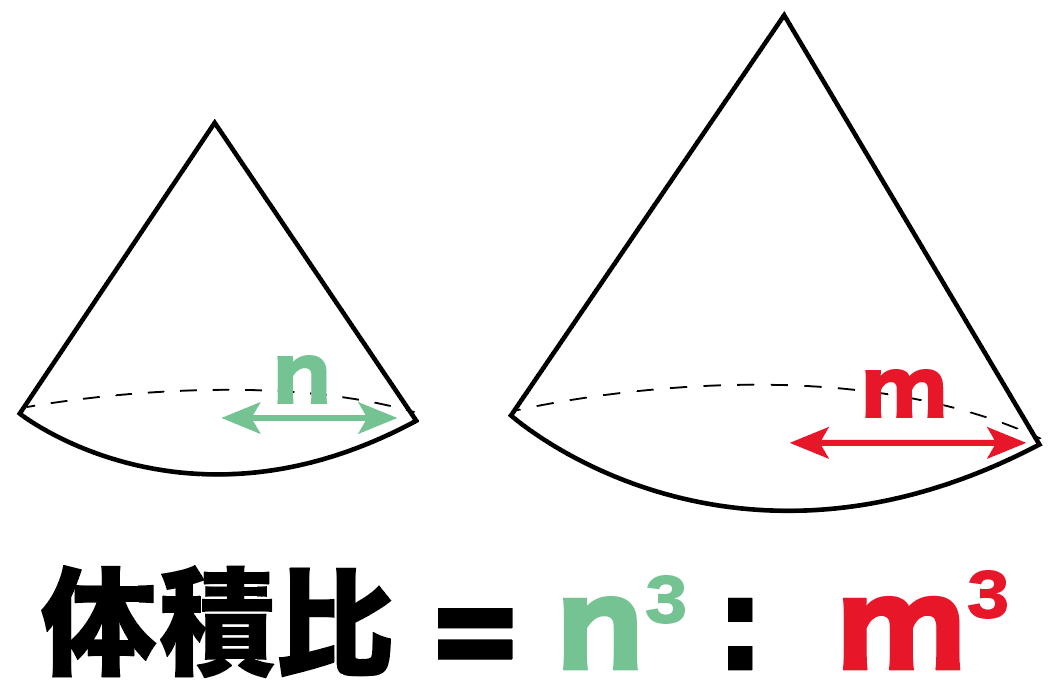
相似と図形

 

相似の利用

 

 

Chapter6. 円の性質

円周角と中心角を使いこなせ！

 

円周角の定理とは？？

 

円周角の定理を使った問題

 

円周角の定理の逆

 

 

Chapter7. 三平方の定理（ピタゴラスの定理）

ピタゴラスが発見した定理を駆使しよう！

 

三平方の定理（ピタゴラスの定理）の公式とは？

 

三平方の定理を使った問題

 

 

Chapter8. 標本調査

統計学の基礎をマスター！

 

全数調査と標本調査

 

無作為に抽出する方法

 

質問する

質問と回答

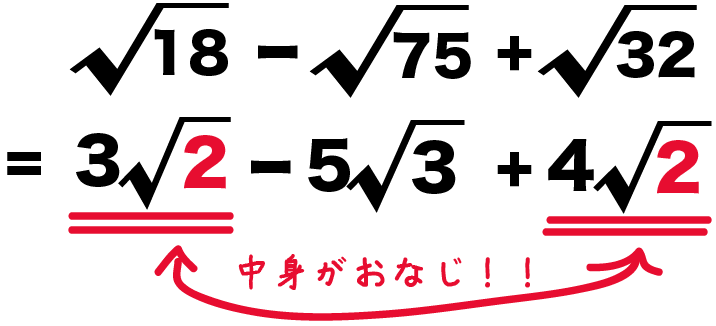
  • 周の長さが60で面積が220㎠の長方形を作るとき、この長方形の2辺の長さを求めようという問題の解き方を教えてください。

  • >周の長さが60で面積が220㎠の長方形を作るとき、この長方形の2辺の長さを求めようという問題の解き方を教えてください。

    方程式の文章題の鉄則は、求めたいものを文字で置いてみること。
    今回は辺の長さを出したいから、こいつをxcm（たての長さ）とおこう。
    「周りの長さが60」っていうヒントから、横の長さをxで表してみて。
    あとは、長方形の面積の公式を使って面積に関する方程式を作ればオッケー。
    解き方は二次方程式の解き方を参考にしてみて

  • 相似条件を使った証明問題がどうしてもできません。

    例えば
    　∠bac=90度、∠acb=56度の直角三角形abcの辺ac上の点Dと頂点bを結ぶ線分と、頂点aから辺ｂｃに引いた垂線aeとの交点をｆとしたものとする。aｄ＝aｆのとき、∠abdの大きさを求めろ。

    とか。

    簡単な中１でも解ける問題ならできますが、中２レベルからできなくなり数学の中で一番できない分野です。

  • ＞　∠bac=90度、∠acb=56度の直角三角形abcの辺ac上の点Dと頂点bを結ぶ線分と、頂点aから辺ｂｃに引いた垂線aeとの交点をｆとしたものとする。aｄ＝aｆのとき、∠abdの大きさを求めろ。

    これは二等辺三角形の性質をうまく使ってやればいいね。
    まず、角FADを求めて、三角形AFDが二等辺三角形だから底角は等しい。
    その情報から角ADBが求められるはずだ！
    高学年になってくると過去に勉強して知っているはずのことが増えてくるから、複合問題が多くなるよね。
    このときに大事なのはやはり基礎。1つずつ図形の基本事項をマスターしていこう

  • すみません⤵⤵
    全然関係ないかもですが今、高校受験生で入試問題を解いてみたのですがとにかく間に合いません、、、、。。
    ちなみに長野県入試ですが大門３が関数、大門４が証明問題、と恒例になっています。
    解く順番を変えた方がいいのか、どちらかを完璧に解くべきなか、、、
    パニックです。大門１、２で５０てんでどうしても大門３、４を取らなければいけません。大門１、２はどうにかなっているので大門３、４のアドバイスをお願いします

  • >ちなみに長野県入試ですが大門３が関数、大門４が証明問題、と恒例になっています。
    解く順番を変えた方がいいのか、どちらかを完璧に解くべきなか、、、
    パニックです。大門１、２で５０てんでどうしても大門３、４を取らなければいけません。大門１、２はどうにかなっているので大門３、４のアドバイスをお願いし

    大問の中の初めの1~2問は基本問題が出題されると思うからそこをしっかり取っていこう。
    余った時間で応用問題に思う存分チャレンジするといいよ

  • AB＝4cm，BC＝8cmの長方形ABCDがある。点Pは，辺AB上を秒速1cmでAからBまで動き，点Qは辺AD上を秒速2cmでAからDまで動く。2点P，Qが同時にAを出発してからｘ秒後の△APQの面積をy㎠とするとき，次の問いに答えなさい。

    ⑴ yをｘの式で表しなさい。また，ｘの変域も求めなさい。

    ⑵点P，Qが点Aを出発して3秒後の△APQの面積を求めない。

    という問題です。考え方を教えて下さい(>_<)

  • ＞AB＝4cm，BC＝8cmの長方形ABCDがある。点Pは，辺AB上を秒速1cmでAからBまで動き，点Qは辺AD上を秒速2cmでAからDまで動く。2点P，Qが同時にAを出発してからｘ秒後の△APQの面積をy㎠とするとき，次の問いに答えなさい。

    これは動点の問題だね。
    x秒後のAP,AQの長さをxで表してやって、そいつらから三角形APQの面積を計算してやろう

  • (2x－1)／3＋(3x＋2)／2＝4の答えが分かりません。
    教えていただけると幸いです。

  • 関数y=-xと関数y=a/x(aは定数)について、xの値が2から4まで増加するときの変化の割合が等しいとき、aの値を求めない。の解き方を教えて下さい。

  • y=-xは比例。比例の関数は変化の割合は一定で比例定数。
    あとはy=a/xの変化の割合をaで表してあやって、それがy=-xの比例定数と等しいっていう方程式を作ればオッケー

  • 1/4t^2＝4ーtの答えが分かりません。
    計算しても自分の答えとワークの答えが一緒になりません。

  • 中点連結定理の逆　という言葉を証明で使ってもいいですか？

  • 三平方の定理を利用した折り返しの問題がわかりません。教えてもらってもよろしいですか？

  • 三平方の定理を利用した折り返しの問題がなかなか解けません！
    テストに出るので教えてください！
    折り返しマジわからんぽです！

  • 式を工夫して解きなさいという問題はどうしたらいいですか？

もう1本読んでみる