相似比の求め方をおしえてほしい!!
こんにちは!ぺーたーだよ。
中学3年生で習う相似。
「相似」ってふつうに生活してたら耳にしないよね??
最初はだれもが「ん、相似ってなんだ?」ってなる単元だ。
この単元でいちばん出てくるのは、
相似比を求めるタイプの問題
なんだ。
今日はテストで問題が解けるように、
相似比の求め方を解説していくよ。
よかったら参考にしてみて。
=もくじ=
- そもそも相似・相似比ってなに?
- 相似比の求め方
そもそも相似・相似比ってなんだろう??
相似比の求め方を勉強する前に、まず、
相似とはなにか??
を復習してみようか。
相似な図形とはずばり、
1つの図形の形を変えずに大きくしたり小さくした図形のことだよ。
たとえば、ある△ABCをビックライトでむちゃくちゃでかくした。
その結果、
△DEFができたとしよう。
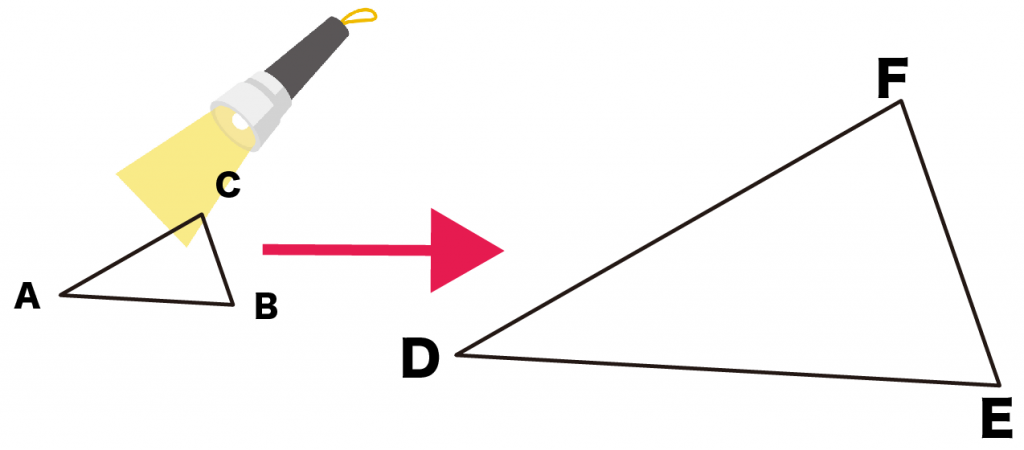
このとき、△ABCと△DEFは相似な図形である
っていえるんだ。
なぜなら、2つの三角形は拡大・縮小の関係にあるからね。
んで、相似比っていうのは、
相似な図形の対応する辺の比
のことなんだよ。
たとえば、△ABCと△DEFの例だったら、
- AB:DE
- BC:EF
- AC:DF
が相似比なんだ。
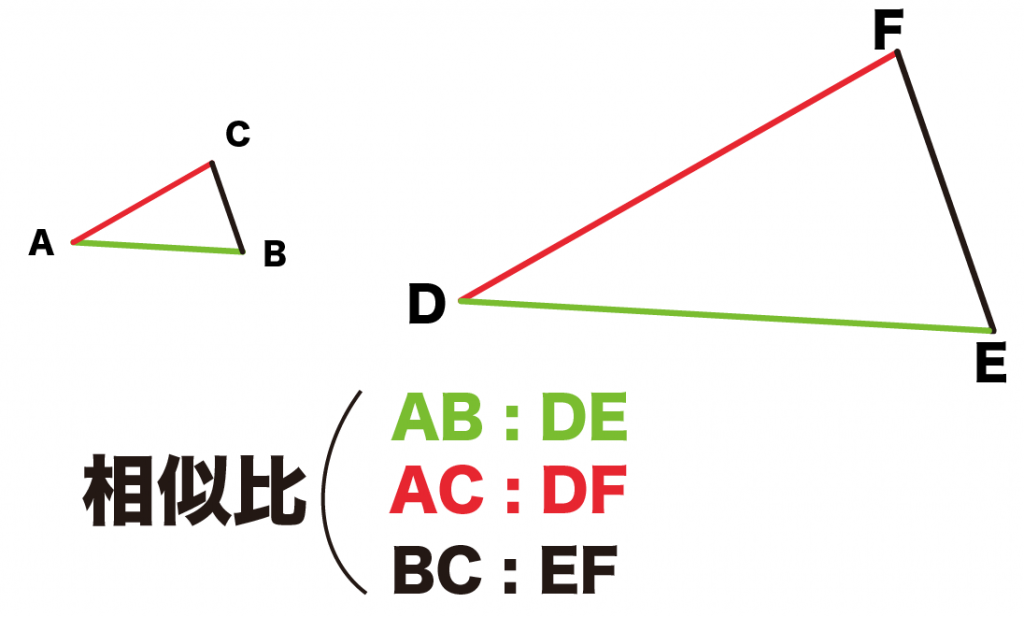
さあ、今回はこの相似比を求め方を解説していくよ。
相似比の求め方がわかる3つのステップ
相似比の求め方はつぎの3つのステップだよ。
- 対応する頂点をさがそう
- 対応する辺の長さを確かめよう
- 比にしてみよう
練習問題をいっしょにといてみよう。
練習問題
下の2つの三角形は相似である。相似比を求めよ。
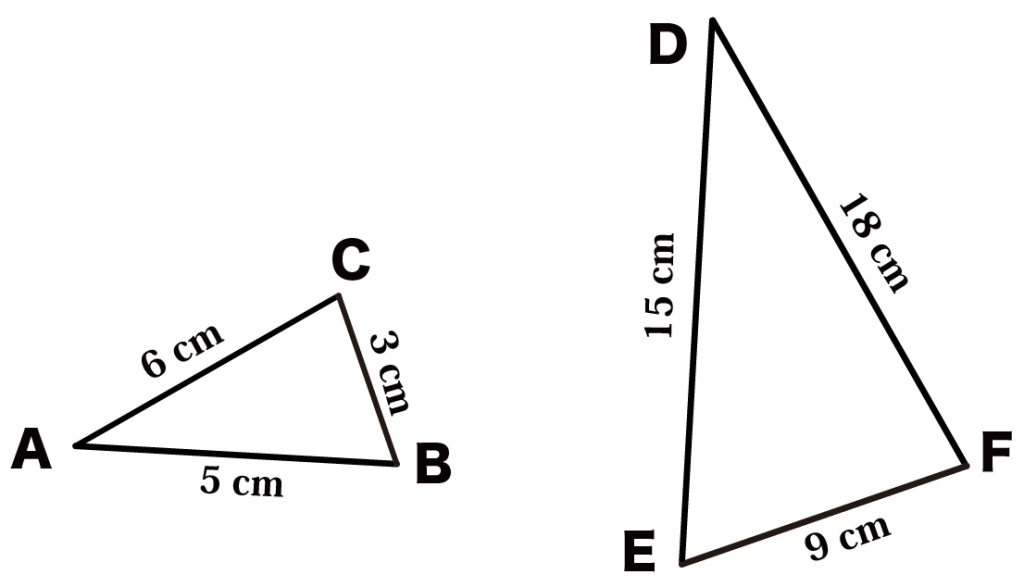
Step1. 図形を頭の中で回転させよう
まず相似な図形の向きをそろえよう。
対応する頂点・辺がかさなるように回転させればいいんだよ。
練習問題をみてみよう。
このままだと対応する辺が見つけにくくない?
その理由は、三角形の向きが同じじゃないからだ。
だから、2つの三角形の向きを同じにしてあげよう!
△DEFを左にぐるっとまわしてやればいいのさ。
そうするとこうなるよ。
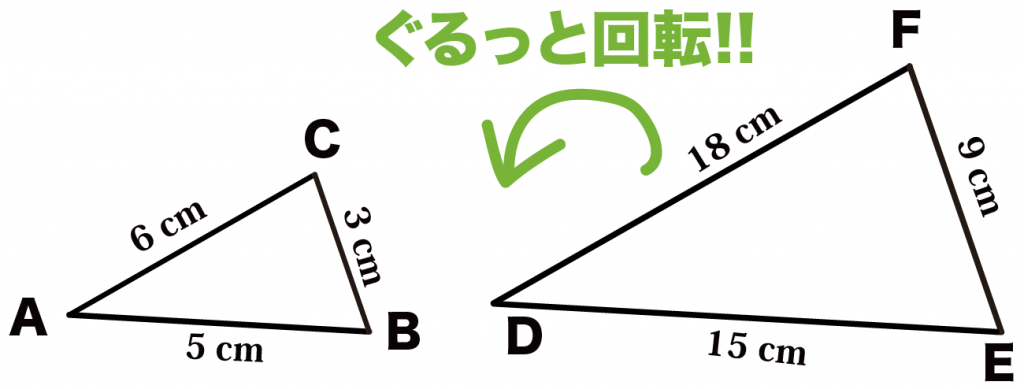
これで対応する辺がみつけやすくなったね^^
Step2. 対応する辺の長さを確かめる
つぎは、対応する辺の長さを確認してみて。
相似比は、
対応する辺の長さの比
だったよね??
だから、相似比を求めるためには、
2つの対応する辺の長さ
を知る必要があるわけ。
練習問題でいうと、
- 辺AB
- 辺DE
が対応する辺だね。
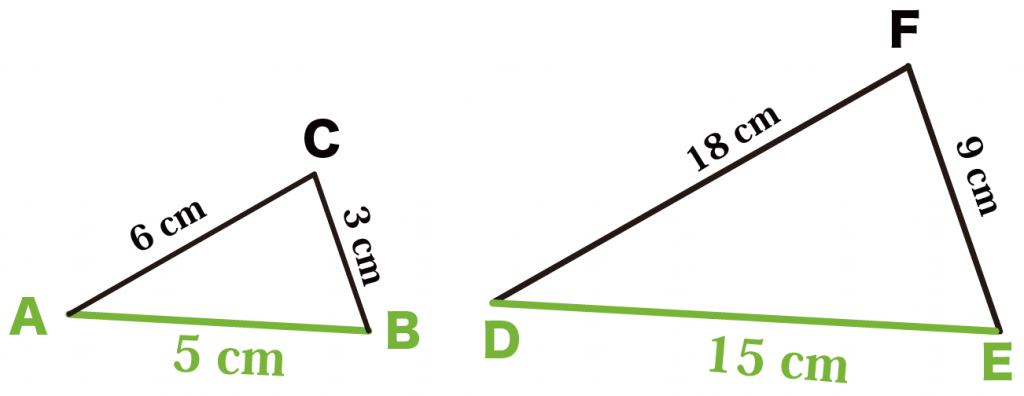
こいつらの長さはそれぞれ、
- 辺AB = 5
- 辺DE = 15
になってるね!
Step3. 相似比を求める
あとは相似比を求めるだけ。
相似比は、
対応する辺の長さの比
だったよね??
だから、もし、2つの相似な図形があったら、
対応する辺1 : 対応する辺2
の比を求めればいいわけ。
練習問題でいうと、△ABCと△DEFの相似比は、
AB : DE
を求めればいいね。
なぜなら、
この2つの辺が対応する辺同士だからね。
- 辺AB = 5
- 辺DE = 15
だったから、
AB : DE
= 5: 15
= 1: 3
になる。
これが2つの三角形の相似比なんだ。
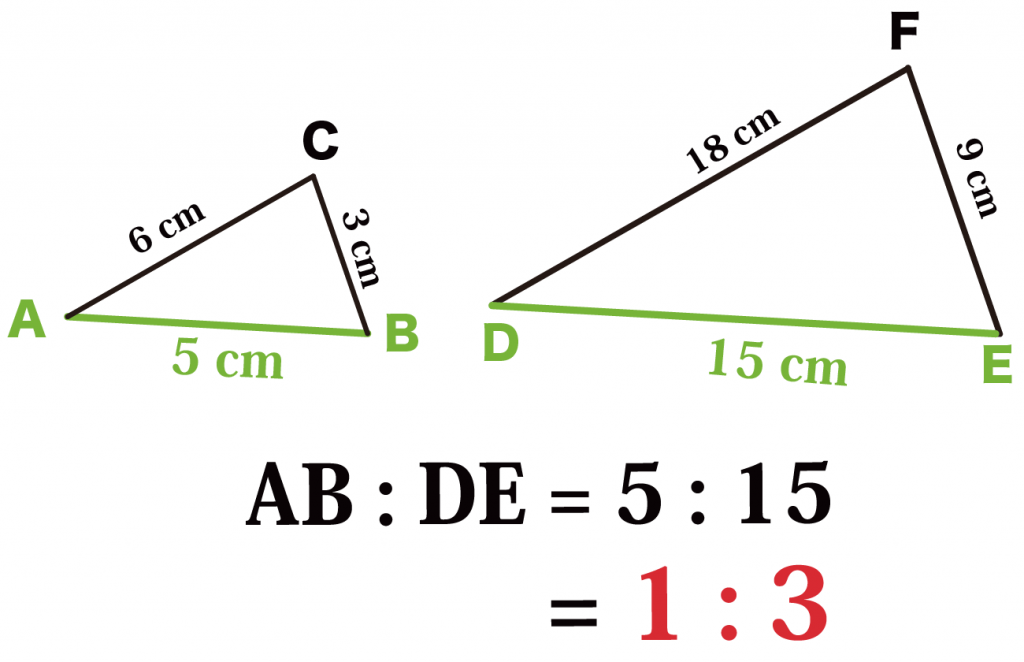
答えるときは一番簡単な整数で答えるよ。
そこだけ注意してね!
他の辺で計算しても1:3になるから安心して。
まとめ:相似の比の求め方は向きをそろえろ!
図形の相似比を求めるには回転させるのがカギ!
頭の中で回転させるイメージ力が必要。
回転させたらノートの余白に描いちゃおうね。
目ですぐに確かめられるから、解く時間を減らすこともできるよ。
相似比は基本的なことだからやり方覚えておいてね。
じゃ、また今度!
ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める


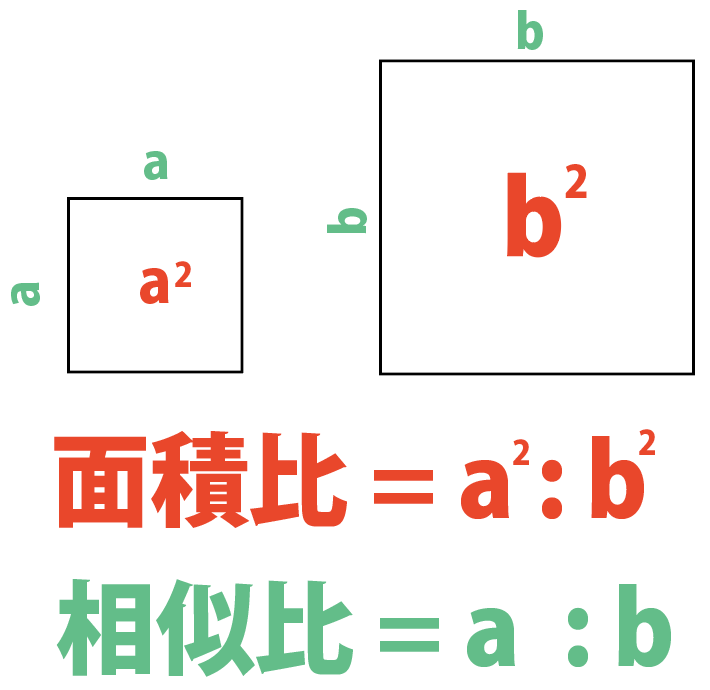
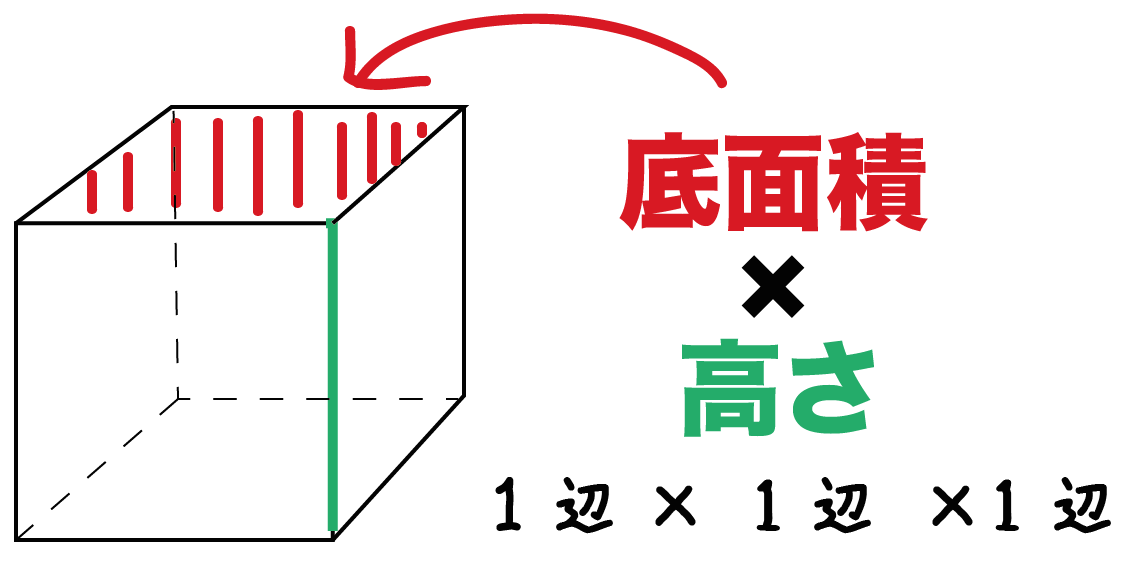

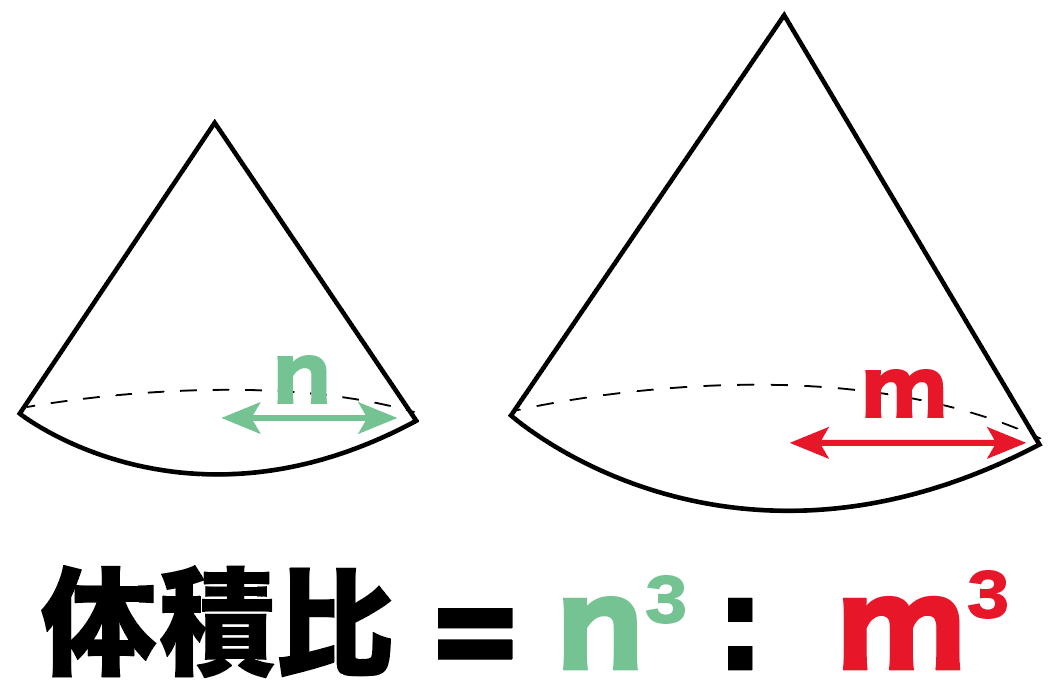

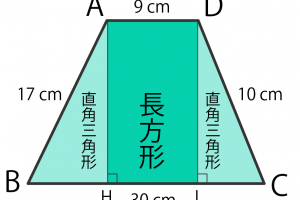
面積比の求め方
三角形の面積の求め方
>面積比の求め方
相似比から面積比を求める方法を読んでみて
三角形の面積の求め方を読んでみて
あるクラスの一学期の女子生徒の数はクラスの人数の5分の3に8人足りませんでした。
2学期から男子が2人、女子が2人転校してきて女子生徒の数はクラスの7分の4になりました。
クラスの人数は何人になりましたか?
の求め方を教えてください。お願いします。
>あるクラスの一学期の女子生徒の数はクラスの人数の5分の3に8人足りませんでした。
2学期から男子が2人、女子が2人転校してきて女子生徒の数はクラスの7分の4になりました。
クラスの人数は何人になりましたか?
転校してくる前のクラスの人数をx人としよう。
そして、転校前の女子の人数をxで表して、そこに女子が2人転校してきて増えた時に、
四人増えたクラス全体の7分の4に等しいっていう等式を作ればいいよ
円の相似比についても教えてください。
>円の相似比についても教えてください。
円も求め方は一緒だよ!
半径がわかってたら、
半径の2乗の相似比になるはず!
角の大きさが違っても相似は求められますか?
>角の大きさが違っても相似は求められますか?
相似条件を満たしてないと相似な図形とは言えないので注意しよう。
相似な図形は角度は等しいはず
次の比をもっとも簡単な整数の比で表せ。
という問題なんですけど、0.32:0.52は
どのように表すことができますか?
>0.32:0.52
それぞれ100倍してあとは、4で割って約分すればいいんじゃないかな
三角形AとBは相似で、
三角形Aの中の三角形cを引いた 三角形Aーc:三角形B
ってどうやって考えますか?
>三角形AとBは相似で、
三角形Aの中の三角形cを引いた 三角形Aーc:三角形B
ってどうやって考えますか?
うーん、三角形Cにもよるかな。問題送ってみて
関数の利用や応用が
いまいち分かりません
平行な線の見つけ方を教えてください
>平行な線の見つけ方を教えてください
同位角や錯角を使うんじゃないかな!
二次方程式のとても分かりやすい解き方を教えて!
>二次方程式のとても分かりやすい解き方を教えて!
二次方程式はいくつか解き方があるから、見分け方を覚えるといいよ。
二次方程式の解き方の見分け方を読んでみて
証明のコツ教えてくださーい!
>証明のコツ教えてくださーい!
証明のコツを読んでみて!
中点連結定理を使った応用問題の解き方を教えて下さい、基礎は出来る自信はありますがこの図形のどこが並行かというのが線が多すぎて見分けがつきません、何かコツとかありますか?
>中点連結定理を使った応用問題の解き方を教えて下さい、基礎は出来る自信はありますがこの図形のどこが並行かというのが線が多すぎて見分けがつきません、何かコツとかありますか?
中点連結定理は応用問題では、三角形の辺の中点を結んだ隠れててわかりにくい線分を見つけるのが鍵かな。
混乱してきた時は、問題の図形に平行とか中点とかの矢印を付けていくといいね
平行線と比の性質の利用で、
「線分AB上にあり、ABを2:1に分ける点Pを求めなさい。」
っていう問題なんですが、どうやったらできますか?
問題によるかな!
作図ではないよね?
証明のやり方を教えてください。
いくらやってもできないんですよ
相似比がわかってる三角形で、いちいち比を書かずに辺の長さを求めるやり方がいまいちわからないので教えてほしいです
例えば、∆ABC ∽∆DEFでAB:4=4:4ルート2
と出ているとき、どういう式をたてればよいのでしょう?
場違いなのですが、相似な図形のXとYを求めるやつってどことどこの辺を使うか知りたいです。
相似比を求める複雑な図形の問題がこのサイトを見ても解けません。複雑な図形の求め方も教えて下さい
高さが同じな三角形は、底辺の比で相似比が決まるんですか?