3分でわかる！相似比から面積比の公式

相似比から面積比を求める公式？？

やあ、ぺーたーだよ。

中3になると、相似を勉強するよね。

覚えること多くて大変。

相似の証明したり、相似比を求めたり…ほんといろいろ。

中でもよくでてくるのが、

相似比から面積比を求める問題。

むずかしそうにみえるけど、公式さえ分かってれば大丈夫。

面積比は絶対に求められる！

今日はこの面積比の公式を紹介していくよ〜

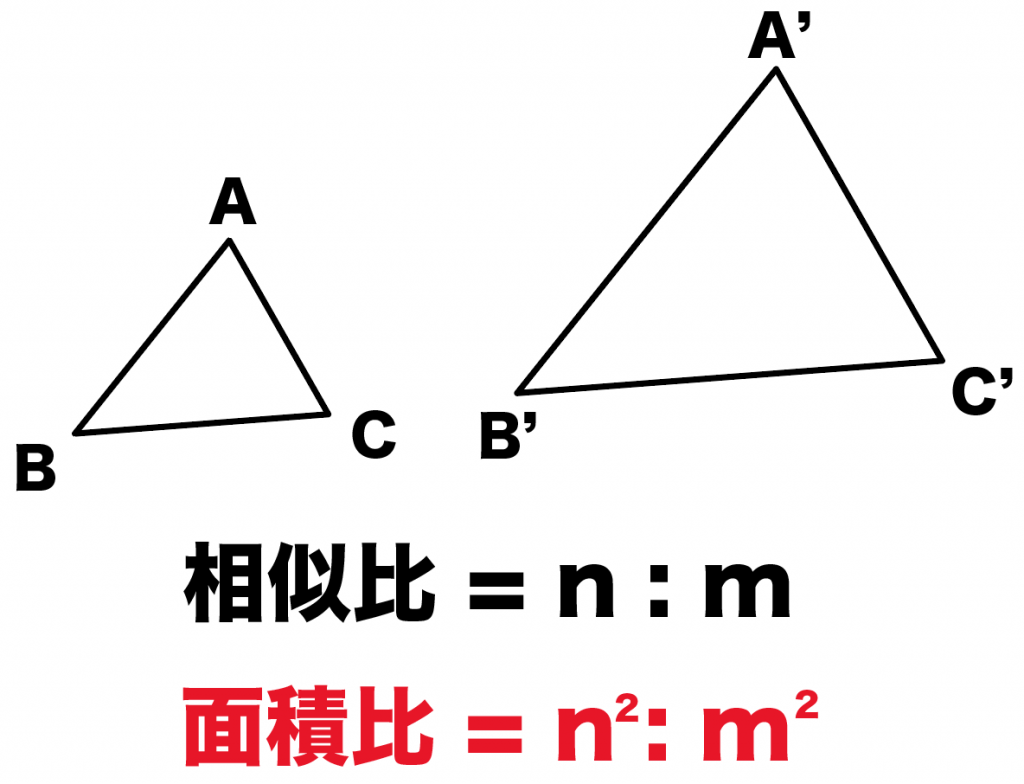
相似比から面積比を計算できる公式

面積比にはつぎの公式があるよ。

「面積比」は「相似比の2乗」になる

ってやつだ。

たとえば、△ABCと△A’B’C’の相似比が「n:m」だとしよう。

このとき面積比は、

n² : m²

になってるんだ。

せっかくだから、この面積比の公式をつかってみよう。

つぎの2つの三角形をイメージしてみて。

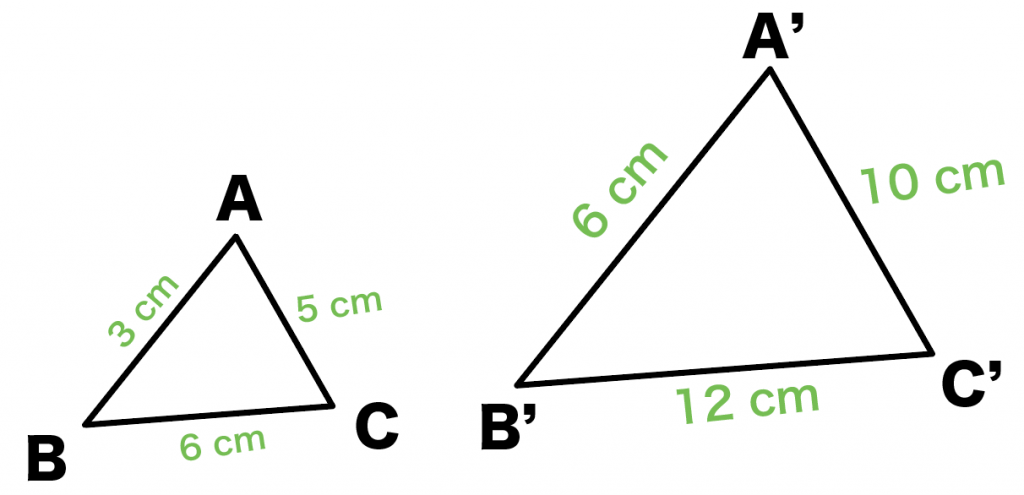
△ABCと△A’B’C’の辺の長さがそれぞれ、

• AB = 3
• BC = 6
• AC = 5

と、

• A’B’ = 6
• B’C’ = 12
• A’C’ = 10

になってるよ。

この2つの三角形の面積比をだしてみよう！

公式なら2ステップで面積比だせちゃうんだ。

1. 相似比を求める
2. 面積比をだす

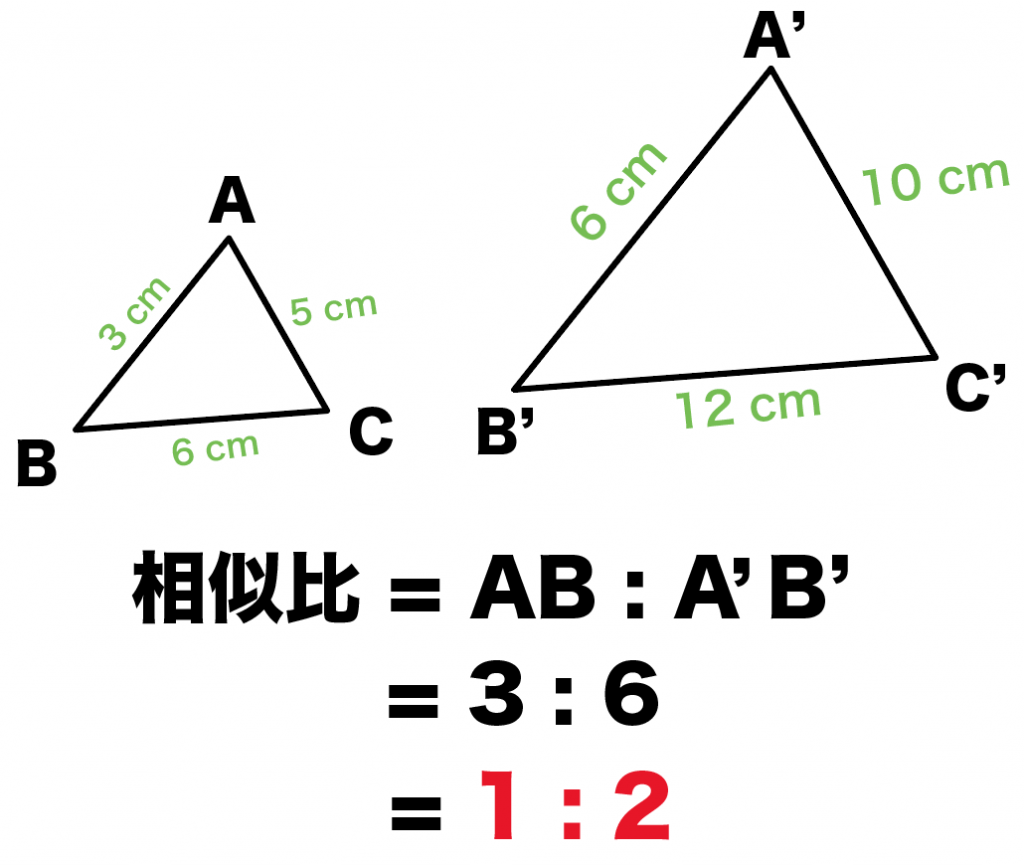
Step1. 相似比を求める

まず相似比を出してやろう！

相似比の求め方は覚えてる？？

相似な図形同士の、

対応する辺の長さの比

を求めればよかったね？？

今回でいうと、辺ABに対応する辺は辺A’B’。

AB=3cm, A’B’=6cmだから、

相似比は、

AB : A’B’
= 3: 6
= 1 :2

になるね。

Step2. 相似比から面積比をだす

相似比が出ちゃえばあとは簡単。

相似比を2乗すれば面積比がでるってわけ。

△ABCと△A’B’C’の相似比は、

1: 2

だったね？？

面積比は2乗してやった比の、
1² : 2²
= 1 : 4

になるはず！

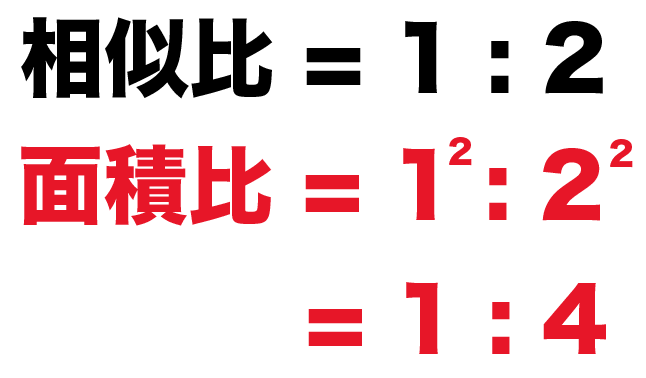
おめでとう！

相似比から面積比を計算できちゃったね。

面積比の公式をつかった問題に挑戦！

面積比の公式でもう1つ問題を解いてみよう。

公式はつかっておぼえるのが一番！

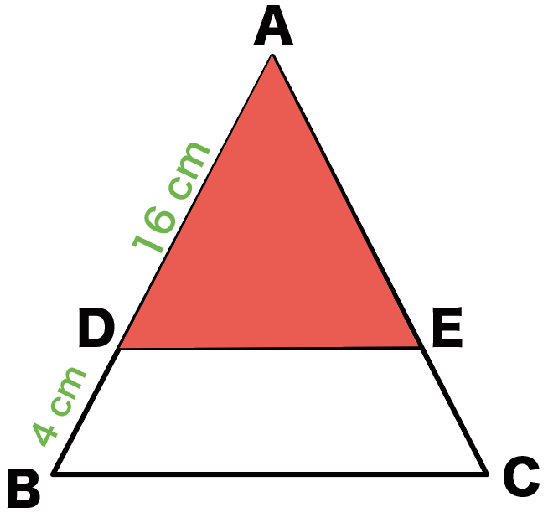
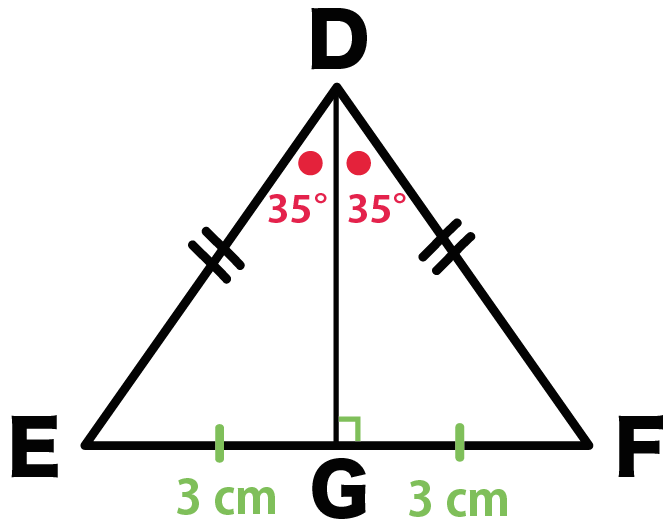
つぎの図の△ABCにおいて、AD = 16cm、DB = 4cmで、

△ADEと△ABCは相似です。

 

 

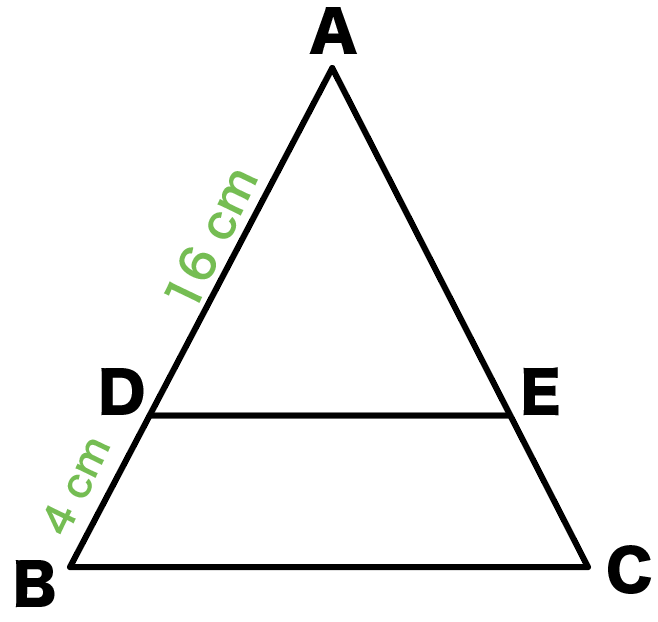
1. 相似比を求めなさい。
2. 面積比を求めなさい。
3. △ABC = 50cm²のとき、△ADEの面積を求めなさい。

問1. 「相似比を求めなさい」

まずは相似比を求めるよ。

この場合、対応する辺は分かるかな？

色で分けるとこうなるよ！

この問題では、ADの長さ（16 cm）が分かっているから、

赤色の辺を使って考えてみよう。

ABの長さはわかるかな？

そう、そうだね。

AB
= AD + DB
= 16 + 4 = 20

になってるはず。

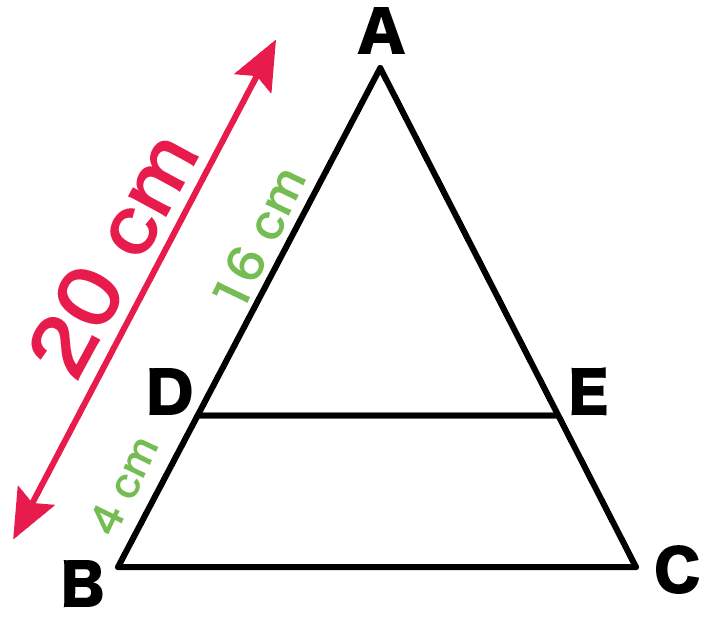
AD=16cm、AB=20cmだから、

相似比は…

△ADE : △ABC
= 16 : 20
= 4:5

だ！

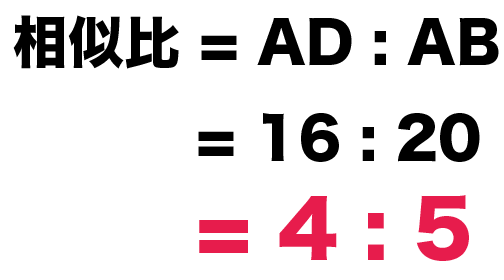
問2. 「面積比をもとめよ！」

面積比はさっきの公式で一発！

面積比は相似比の2乗になる

だったよね？？

この公式をあてはめると、

面積比
= 4² : 5²
= 16 : 25

になるね。

ってことで、答えは16:25！

問3. 「△ABC = 50cm² のとき、△ADEの面積もとめて」

最後は△ADEの面積だ。

さっきの面積比で求めていくよ。

△ADEの面積がわからないから、ｘ[ cm²] とでもしておこう。

んで、

△ADEの面積：△ABCの面積 = 面積比

っていう比例式をつくってみようぜ。

• 面積比が16:25
• △ADE=x [cm²]
• △ABC=50 [cm²]

だから、比例式は、

△ADEの面積：△ABCの面積 = 16 : 25

x : 50 = 16 : 25

になるね。

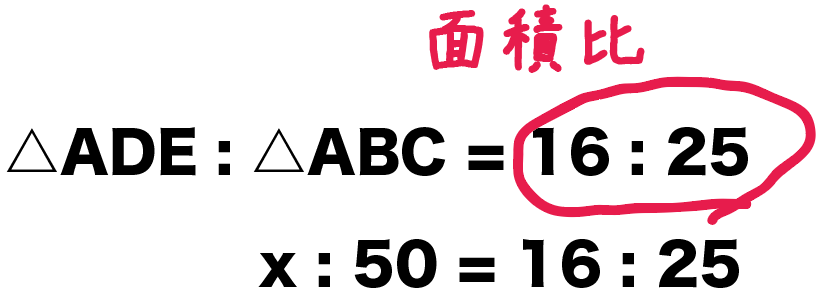
比例式の解き方でといてやると、

x : 50 = 16 : 25

25 x = 16×50

x = 32 [cm²]

になる。

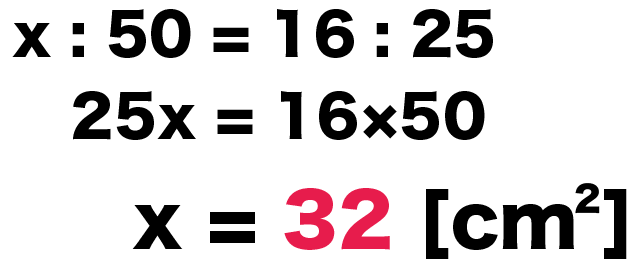
つまり、

△ADEの面積は32 [cm²]ってわけ！

まとめ：相似比で面積比の公式をつかえば一発！

相似比で面積比もとめられた？？

相似比の2乗が面積比になる

っていう公式さえおぼえてれば怖くない。

面積比を求める問題はきっと大丈夫！

じゃ、またね！

ぺーたー

ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める