Ken

数学の証明問題の解き方がわかる4つのステップ

数学の証明問題の解き方がわからない！

こんにちは！この記事をかいているKenだよ。生姜焼き、食べ過ぎたね。

 

数学の証明問題ってむずいよね？？

計算問題とはひと味ちがう。

どうやって解いたらいいのかわからない。

このままでは数学が嫌いになっちゃいそうだよ・・・・

数学　証明問題　解き方

そこで今日は、

中2数学で勉強する証明問題の解き方を4ステップで解説していくよ。

よかったら参考にしてみてね^^

 

 

数学の証明問題の解き方がわかる4つのステップ

例題の証明をときながらみていこう！

 

AB = DC、AB // DCの△ABCと△CDAがあったとします。

このとき、角ABC = 角CDAであることを証明しなさい。

 

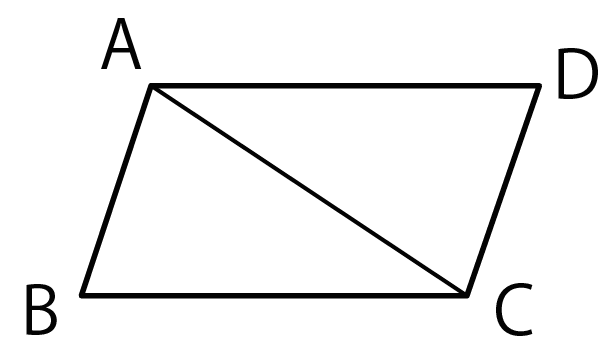
証明問題　コツ

 

 

Step1. 仮定と結論を整理する！

まずは仮定と結論を整理しよう。

仮定と結論って簡単にいってしまうと、

  • 「仮定」＝「問題文からすでにわかっていること」
  • 「結論」＝「証明のゴール」

だよ。

証明問題において、

なにを説明できればゲームクリアなのか？？

そのために、どんな条件があたえられているのか？？？

を整理することはむちゃ大事なんだ。

 

例題で実際に、

仮定と結論を整理してみよう。

 

AB = DC、AB // DCの△ABCと△CDAがあったとします。

このとき、角ABC = 角CDAであることを証明しなさい。

証明問題　コツ

 

  • AB = DC
  • AB//DC

は問題文でわかっていることだね。

つまり、こいつらが「仮定」さ。

 

一方、結論は、

  • 角ABC = 角CDA

だ。

 

証明問題の「結論」って、

○○であることを証明しなさい

の「○○」にかいてあることが多いよ。

数学　証明　解き方

どうしても結論がみつからないときは、

問題文を読み返してみてね。

 

 

Step2. 仮定を図にかきこむ！

仮定を図にかきこんでやろう。

かきこむだけで、

仮定と結論がわかりやすく整理できて、

解き方のイメージをしやすくなるんだ。

ただここで注意してほしいのは、

仮定と結論をごっちゃまぜにしないことだ！

 

同じ黒ペンで仮定と結論をかきこむのはNG。

仮定と結論がどっちなのかわからなくなるからね。

 

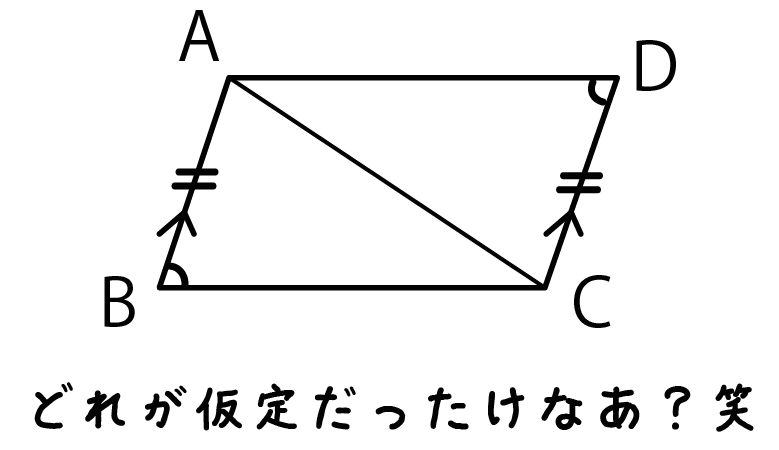
数学　証明問題　コツ

 

だから、

仮定と結論を色違いのペンで書き込むことをおすすめするよ。

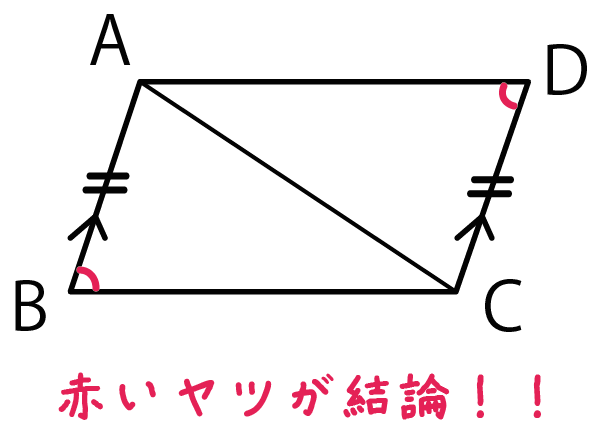
中2数学　証明問題　コツ

 

えっ、書き込まなくてもすでに整理できてるって？？

そういうヤツはこのステップをとばしてくれ。

つぎにいこう！

 

 

Step3. 結論までの道のりをイメージする

仮定・結論をみつめて、

どうやって仮定から結論までもっていくか？？

をイメージするんだ。

中2数学　証明問題

具体的にいうと、

結論をいうために、

「根拠となることがら」は何をつかうか？？

を考えることになるよ。

 

例題をみてみよう。

例題の結論は、

角ABC = 角CDA

だったよね？

中2数学　証明問題　コツ

うーん、

どうしよー、

うーん、

・・・・・

は！

これだ！

△ABCと△DACが合同であることをいえば

「角ABC = 角CDA」がいえるかも！！

合同な図形同士の対応する角の大きさが等しい

って根拠をつかえばね。

 

 

って感じで、

どの根拠をつかえばゴールの結論にたどり着けるか？

を事前にイメージしていくんだ。

 

 

Step4. 書き方にどおりにかく！

後は証明を書くだけ！

証明の書き方には型がある。

それ通りにかいていけばいいんだ。

数学　証明問題　解き方

 

証明の書き方はつぎのようになっているよ。

  1. 問題文でわかっていること（仮定）
  2. 仮定からわかること
  3. 根拠となることがら
  4. 結論

この4つを詰め込んでやれば大丈夫だよ。

書き方は先生によって違うから、

担当教師の書き方をマネしてみてね笑

 

例題の答えをかいてみるよ。

ぼくだったらつぎのような感じでかくね。

 

△ABCと△CDAにおいて、

AB = CD (仮定)・・・(1)
AC = CA (共通)・・・(2)

AB // CDより、
平行線の錯角が等しいので、
角BAC = 角DCA・・・(3)

(1)、(2)、(3)より、
2辺とその間の角がそれぞれ等しいので、△ABC ≡ △CAD対応する角の大きさが等しいので、角ABC = 角CDA

となる。

 

問題でわかっていること（仮定）から、

証明問題のゴール（結論）をみちびければいいんだ。

 

 

まとめ：数学の証明問題の解き方は整理とイメージが大事！

数学の証明問題の解き方はつぎの4ステップだったね。

  1. 仮定と結論の整理
  2. 仮定を図にかきこむ
  3. 結論までをイメージする
  4. 書き方にしたがってかく！

証明問題はちょっとむずい。

だけど、解き方さえおさえておけば大丈夫さ。

問題をといて証明になれてみてね^^

そんじゃねー

Ken

質問する

質問と回答

  • 三角形の証明で、二つの合同な三角形が二つ繋がったもので、その共通する辺をACとして
    ACは2つの三角形に共通な変だから
    AC=ACとなりますが問題や答えによってAC=CAとなっている場合がありますがどちらが正しいですか？

  • >三角形の証明で、二つの合同な三角形が二つ繋がったもので、その共通する辺をACとして
    ACは2つの三角形に共通な変だから
    AC=ACとなりますが問題や答えによってAC=CAとなっている場合がありますがどちらが正しいですか？

    対応する辺の順番によって異なるね。
    △ABC≡△ADCだったらAC＝ACだし、
    △ABC≡△CFAだったらAC=CAだ。
    対応する辺の順番もややこしいけど注意しよう！

  • 証明がわかりません…
    明日テストなのに…
    教えてください！！！

  • どこから手つければいいのか迷って、10分経過…
    ((そもそも、書き出しを分かってない、、
    結局、ひとりで解けずにこういう解説見てノートに写すだけ…
    もう、何回も書いて覚えるしかないですよね？(笑)

  • >どこから手つければいいのか迷って、10分経過…
    ((そもそも、書き出しを分かってない、、
    結局、ひとりで解けずにこういう解説見てノートに写すだけ…
    もう、何回も書いて覚えるしかないですよね？(笑)

    最初はみんなわからんけど、問題を解くにつれて慣れていくよ！
    解説を見てマスターした問題を時間をおいてもう一度解いてみよう！

  • 証明でも、①～②くらいまでのものなら解けるのですが、④とか⑥まで出てくると解けません。どうすればそこまで簡単に導けられますか。

  • 証明問題の問題文に仮定が書かれていない場合は、どうすれば解けるんですか？
    また、(2)の問題で、「(1)で証明したことをもとに、〜となることを、証明しなさい。」
    というパターンは、どう証明していけば良いんでしょうか、教えて頂かたら幸いです

  • 等積変形の問題で、「△ABCと面積が等しい三角形を、全て答えなさい。」と問われた時の答え方は、証明問題と同じように対応順に書いた方が良いですか？それともアルファベット順でしょうか。

  • ＞証明でも、①～②くらいまでのものなら解けるのですが、④とか⑥まで出てくると解けません。どうすればそこまで簡単に導けられますか。

    材料が増えるのは大抵、辺が等しいことを言うために三角形の合同を証明しなくちゃいけない時とかだよね。
    こう言う時はその目的の「辺が等しいことを言う」に注目していれば、証明の材料が増えても混乱しないはず！

  • ＞証明問題の問題文に仮定が書かれていない場合は、どうすれば解けるんですか？
    また、(2)の問題で、「(1)で証明したことをもとに、〜となることを、証明しなさい。」
    というパターンは、どう証明していけば良いんでしょうか、教えて頂かたら幸いです

    仮定というあからさまな形じゃなくても、必ず証明問題には仮定が隠れているよ。
    たとえば、「平行四辺形ABCDは」という文章だけでも「四角形ABCDは平行四辺形である」という仮定が隠れてるし。
    「(1)で証明したことをもとに」って時は（１）の結論を仮定として証明するよ

  • ＞等積変形の問題で、「△ABCと面積が等しい三角形を、全て答えなさい。」と問われた時の答え方は、証明問題と同じように対応順に書いた方が良いですか？それともアルファベット順でしょうか

    この場合、順番は適当でいいよ。なぜなら、合同でも相似でもないし対応している辺とかないからね

  • >難しい証明の問題を簡単に解く方法を教えてください！

    難しい証明は、あることを証明して、それを使って新たな証明をしていくパターンが多いね。
    だから、難しい問題を解くためには基本レベルが解けるかどうかが鍵となってくるのね

  • 証明で角についてふれるときは、錯角・同位角・対頂角以外は使えないんですか？

  • >証明で角についてふれるときは、錯角・同位角・対頂角以外は使えないんですか？

    そんなことないよ。何でもあり

  • >覚え方などは、あるのでしょうか？

    証明は覚えるより慣れた方が早い！

  • 証明問題に慣れるためには何から始めれば良いですか？

  • >証明問題に慣れるためには何から始めれば良いですか？

    図形の基本事項を覚えることかな！
    あとは問題をたくさんといて証明の形式に慣れよう！

  • いつも参考にさせて頂いております。
    証明の書き方は理解しているのですが、
    「証明するためには何を使えばいいか」
    という根本的なところでいつもつまずいてしまいます。
    もう一歩踏み込まなければならない問題などでは完全にパニックになってしまい
    どんなに問題集を解いて先生に質問しても
    テストで全然点数が取れなくて
    証明問題に苦手意識を持ってしまいました。
    その証明に必要な条件などを明確に出来る方法(こういう図形が出てきたら○○の合同条件を使うetc…)などがありましたらご教示願います。
    質問が分かりにくかったらすみません…

  • >いつも参考にさせて頂いております。
    証明の書き方は理解しているのですが、
    「証明するためには何を使えばいいか」
    という根本的なところでいつもつまずいてしまいます。
    もう一歩踏み込まなければならない問題などでは完全にパニックになってしまい
    どんなに問題集を解いて先生に質問しても
    テストで全然点数が取れなくて
    証明問題に苦手意識を持ってしまいました。
    その証明に必要な条件などを明確に出来る方法(こういう図形が出てきたら○○の合同条件を使うetc…)などがありましたらご教示願います。
    質問が分かりにくかったらすみません…

    丁寧に質問ありがとう！
    証明に使える道具は多く持っておくに越したことはないね。
    多分、まだ道具（合同条件とか）が覚え切れてなくていざという時に引き出しから出てこないのかもしれない。
    そういう時は、
    1. 道具を徹底的に覚える（単語帳を使ってもいい）
    2. 道具を実際に使ってみる（答えを見ながらでもいいから１から証明してみる）
    という練習が必要だね！
    練習を続けていけばパニックになる状態を脱することができるはず。頑張ろうぜ！

  • 本当に数学の証明の考え方がわかんないです。
    教えてください！
    テスト一週間前です

  • 証明がマジでわからないです。明日テストなのでどうすればいいのか教えてください！

  • 書く順番は覚えるしかないね。お手本を参考にしよう。
    ただ、どの証明も書き方は同じだから問題を解いていくと慣れていくよ。
    焦らずに数をこなさそう

  • 折り目の問題が意味不明な状態です。
    どうしたらいいんですか？
    今、大変です。

  • kenさんは、どうやって数学の勉強をしていますか？
    私は、全然ダメで、今いろんな人の意見を聞いています。
    教えて下さい！

  • 基礎をしっかり理解した後に問題を解いて体で覚えるかな！
    知識をものにするには実際にやってみることも大事

  • 折り目の問題は、折ってできた前後の図形が合同ってところがミソだね

  • しょうがくせいです
    しょうめいの問題を(相似)がすらすらと解けるこはなんですか？
    おしえて下さい。

  • 初めまして受験生の母をしてます。
    証明は高校入試に出ますか？

もう1本読んでみる