【中2数学】式の値を求める3つのステップ

中2数学の「式の値」の問題がむずい？？

こんにちは！この記事をかいているKenだよ。カラオケもいいね。

中2数学でh「式の値」っていうやっかいなヤツがでてくる。

「式の値」の問題って、

文字式の中の「文字」に数字をいれたときの値を求める

っていうやつなんだ。

文字に数字をいれて計算するだけ！

慣れれば簡単だからガンガン点をとっていこう。

今日は中2数学ででてくる、

「文字が2つ以上登場する」式の値の問題

を解説していくよ。

よかったら参考にしてみて^^

中2数学の「式の値」がわかる3ステップ

さっそく「式の値」の解き方をみていこう。

つぎの例題をといてみよう！

この手の問題は3ステップでちょちょいのチョイさ。

Step1. 分配法則で（）をはずす！

文字式を簡単にしてあげよう！

チョー簡単な式はそのままでいいんだけど、

（）のついた式はもう少しシンプルにしちゃおう。

例題の文字式をみると、

(8a + 3b) -2(3a-7b+1)

って感じで（）で文字式が太っているよね？？

とてもじゃないけどスリムなんかじゃない。

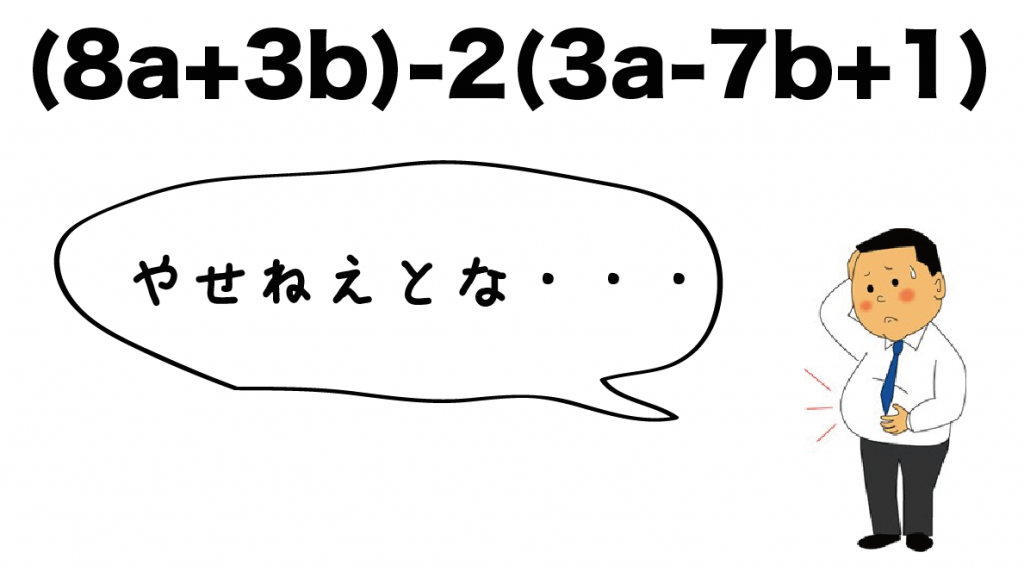
(8a + 3b) -2(3a-7b+1)

をスリムにするために分配法則をつかってあげよう。

すると、

(8a + 3b) -2(3a-7b+1)

= 8a + 3b -6a + 14b -2

になるね！

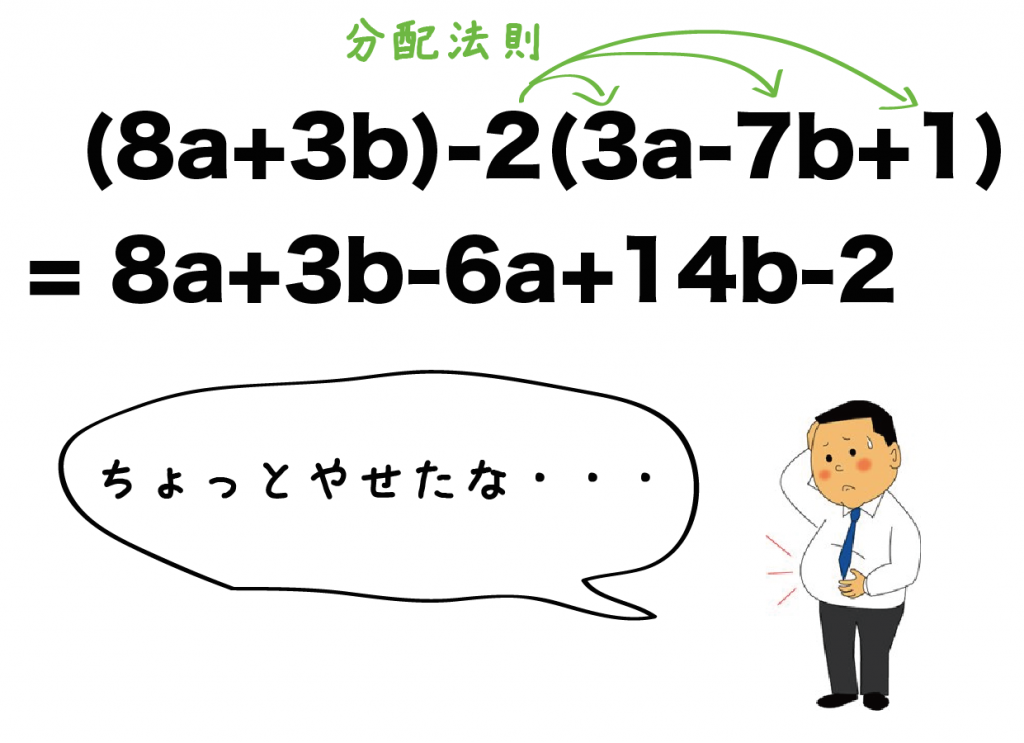
どう？？だいぶスリムになったよね？笑

Step2. 同類項をまとめる！

文字式の（）をはずしただけじゃまだスリムじゃない。

式は横に長いし、どうにかしてあげたくなるよね？笑

つぎはもっとシンプルにするために、

同類項をまとめる

っていう荒技で勝負してみよう。

※　同類項のまとめ方の記事

例題でちょっと簡単にした、

8a + 3b -6a + 14b -2

という式にはつぎの3種類の項があるよね？

• 　a
•     b
• 数字

同じ文字の項は係数をたしてみよう。

すると、

2a +17b -2

って感じで文字式がスリムになったでしょ？？

Step3. 数字を代入する！

最後に文字に数字を代入してみよう。

どんな数字を入れればいいのか

ってことは問題にかいてあるよ。

この例題では、

• a = 3/2
• b = -2/17

って問題で指定されているよね？

こいつらをStep2で計算した超スリムな文字式に代入してあげよう。

すると、

2a +17b -2

= 2 × 3/2 + 17×(-2/17) -2

=  3 + (-2) -2

= -1

っていう式の値が求まるね！

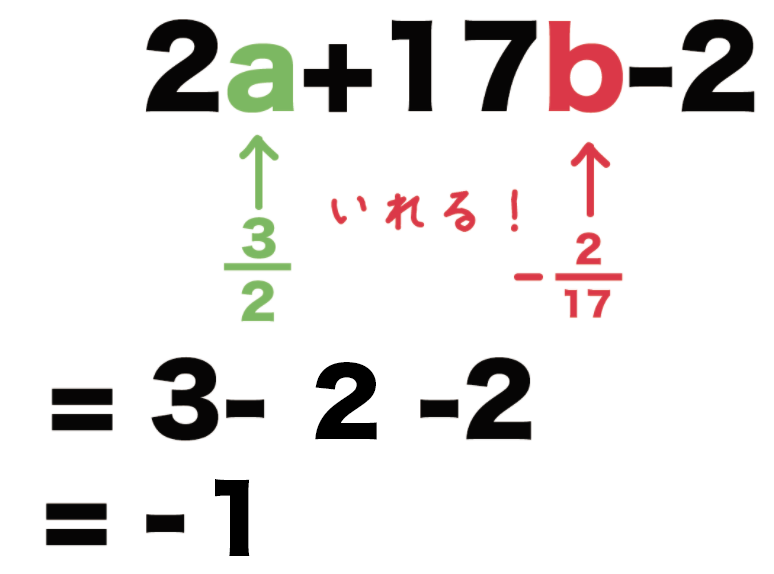
おめでとう。これで「式の値」もマスターしたね^^

まとめ：「式の値」を求める前には文字式をスリムに！

式の値を求める前には必ず、

文字式をできる限りカンタンにする

ってことを忘れずにね！

これなら焦らずに式の値を計算できるはず！

テスト前にもう一度復習してみてね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。