【中学数学】二次関数y=ax2のグラフから式を3秒で読み取る方法

 二次関数y=ax2のグラフから式を読み取る？！

こんにちは！この記事をかいているKenだよ。ジンジャーは心にきくね。

中3数学では、

二次関数y=ax2を勉強していくよ。

ここではあろうことか、いろんな問題が出題される。

二次関数の比例定数を求める問題とか、

グラフをかく問題とか、

xとyの変域を求める問題とかね。

もう、ほんとたくさん。

そんな中でもとっつきやすいのが、

y=ax2のグラフから関数の式を読み取る問題

だ。

手頃でしれっと解けちゃうから、得点源になるはず。

この記事でしっかりマスターしておこう。

二次関数y=ax2のグラフから式を読み取る問題の解き方

たとえばつぎのような問題だ。

この手の問題は3ステップでとけちゃうよ。

• x・y座標が正確に読み取れる点をさがす
• y = ax2に座標を代入
• 一次方程式を解く

Step1.「 x・y座標が読み取れる点」をさがす

まず、

x・y座標が正確に読み取れる点

をさがしてみよう。

もし、座標のメモリの単位が「1」だとしたら、

x・y座標がともに整数になってる点をさがせばいいのさ。

例題のメモリの単位も「1」だよね？？

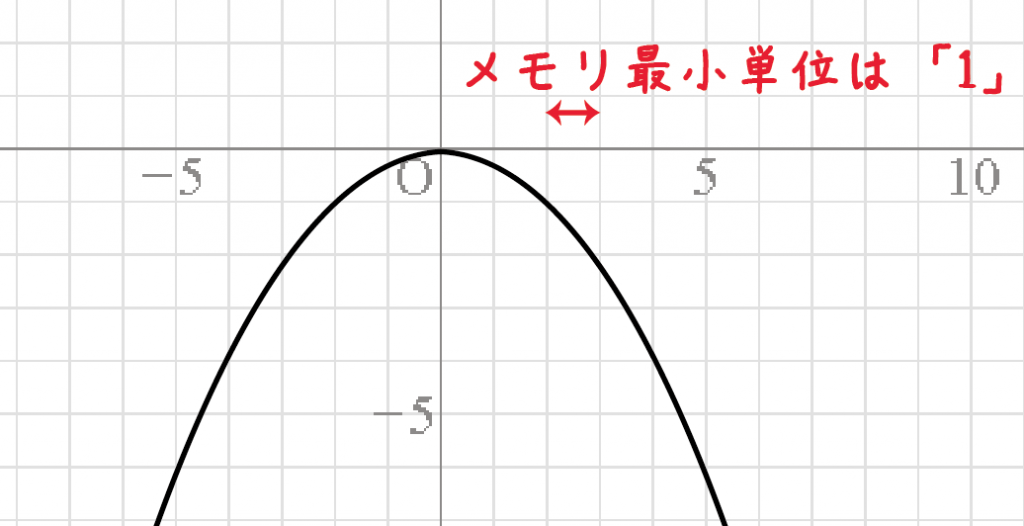
ってことは、xとyの座標が整数の点をさがせばいい。

よーく目をこらしてみてみると、

・・・・・・・・・・・

はっ！

この放物線、

（2, -1）

とおってねえ？

こんなかんじで、xとyのメモリの交点を通っていて、

座標を読み取れる点をさがせばいいのさ。

Step2. 「y = ax2」に座標を代入

さっき読み取ったx、y座標を二次関数y=ax2に代入しよう。

• x 座標 ⇒ xに代入
• y 座標 ⇒ yに代入

っていったかんじで代入してみて。

練習問題では、

• x 座標 ：2
• y 座標 ：-1

になってたよね？？

この座標たちをy= ax2に代入してみると、

-1 = a × (2)^2

-1 = 4a

になる。

Step3. 一次方程式を解く

あとは一次方程式を解くだけ。

xとyの座標を二次関数y=ax2に代入すると、

aに関する1次方程式ができるはず。

こいつを方程式の解き方通りにといてやればいいのよ。

練習問題でのこった一次方程式は、

-1 = 4a

だね？？

こいつをaについて解いてやると、

a = -4分の1

になる。

よって、このグラフの二次関数y= ax2の式は、

y = -4分の1 x^2

になるね。

おめでとう！

これでy =ax2のグラフから式を読み取れたね。

二次関数y=ax2のグラフから式を読み取るには目をこらせ！

二次関数y=ax2のグラフから式を読み取れるようになったかな？？

解き方の最大のコツは、

座標を正確に読み取ること。

これにつきる。

ここで間違えると、一次方程式も意味をなさなくなっちゃうからね。

遠視の人はめがねをかけてでもいいから、

正確に座標をゲットしてみよう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。