【中学数学】円の接線をサクッと作図する2つの方法

円の接線の作図がむちゃくちゃめんどっ！

こんにちは、この記事をかいてるKenだよー！　ボタンを掛け違えてちまったね。

円の接線って知ってる？？

「直線と円が一点で交わっていること」を「接する」っていって、

さらに、その直線のことを「接線」、直線と円がまじわっている点のことを「接点」とよぶんだったね。

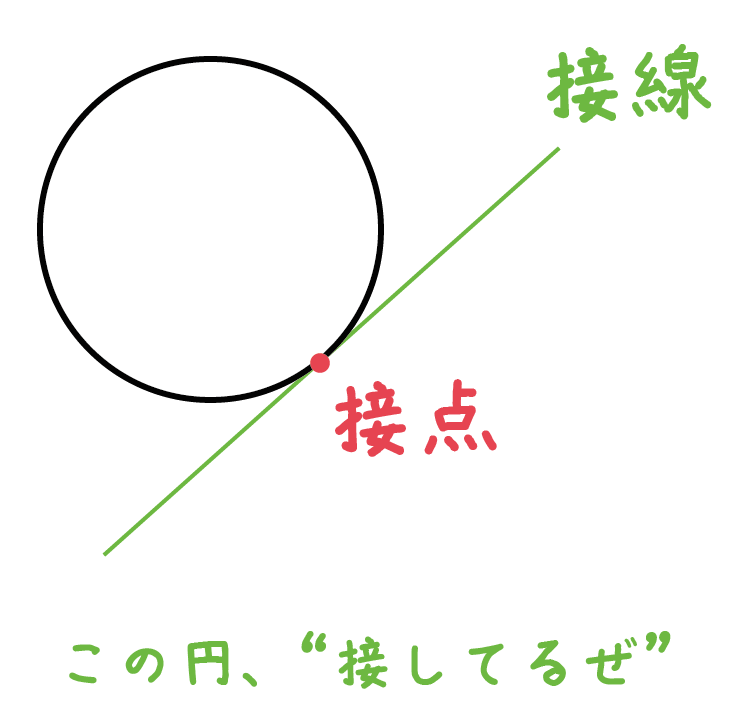
今日は、この「円の接線」の作図方法を解説していくよ。テスト前に確認してみてね^^

~もくじ~

1. 円の接線の作図問題にみられる2つのパターン
2. 円周上の点をとおる接線を作図する問題
3. 外部の点をとおる接線を作図する問題

円の接線作図は2つのパターンしかない？？

「円の接線の作図」ってヤッカイそうだよね？？？

だけど、コイツらは意外にシンプル。

だいたい2つの種類にわけられるるんだ。「接線が通る点」の位置がちょっと違うだけさ。

1. 「円周上の点」を通る接線の作図
2. 「外部の点」をとおる接線の作図

「円周上の点」を通る接線の作図では1本の接線、

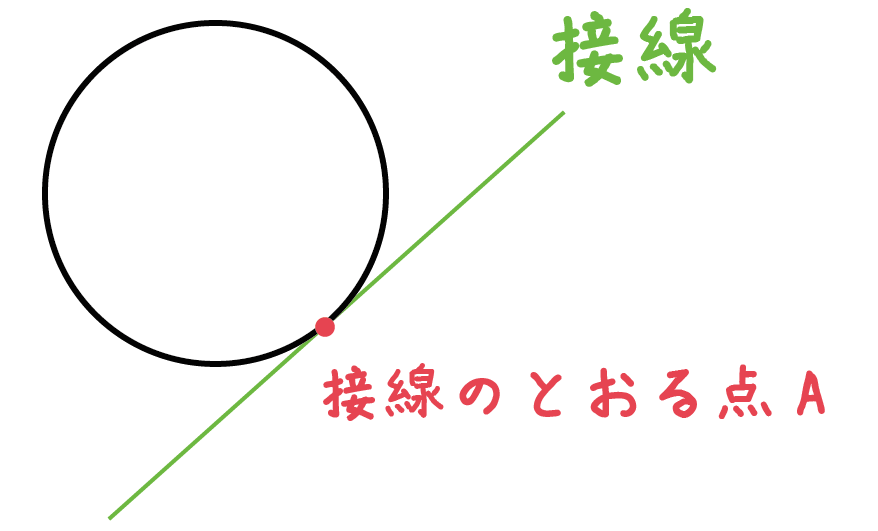
「外部の点」をとおる作図では2本の接線をひくことができるよ。

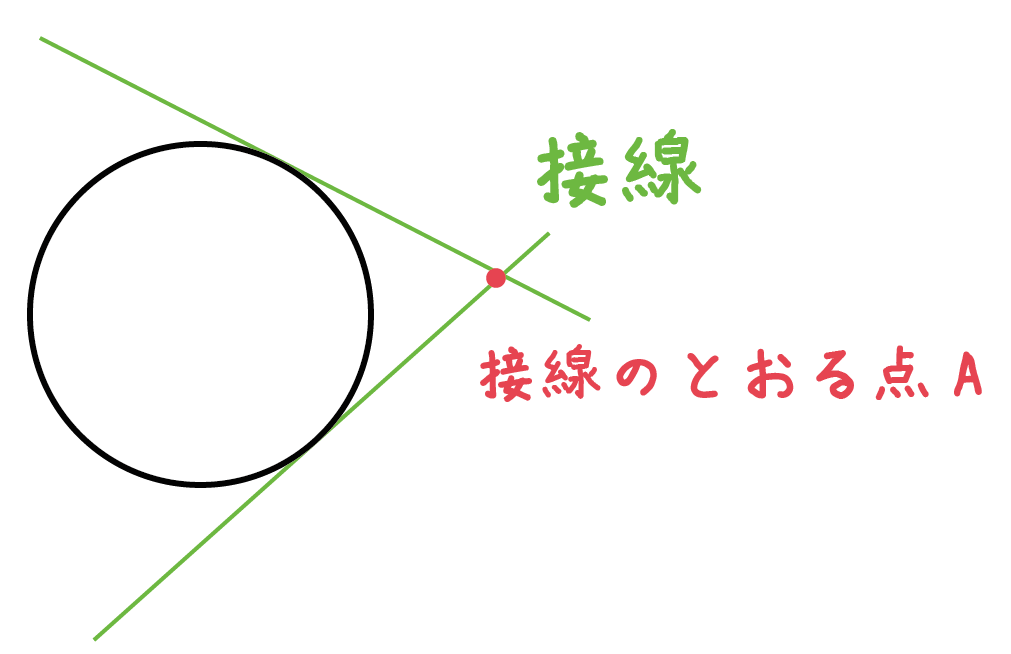
今日は2つの作図方法を確認していこう。作図のために必要なアイテムは、

1. コンパス
2. 定規

だよ。準備はいいねー？？

「円周上の1点」をとおる円の接線の作図

「円周上の1点をとおる」円の接線の作図からだね。

これは教科書にものっている基本の作図方法さ。

例題で作図をじっさいにしながら確認していこう。

例題。

点Aが接線となるように、この円の接線を作図しなさい。

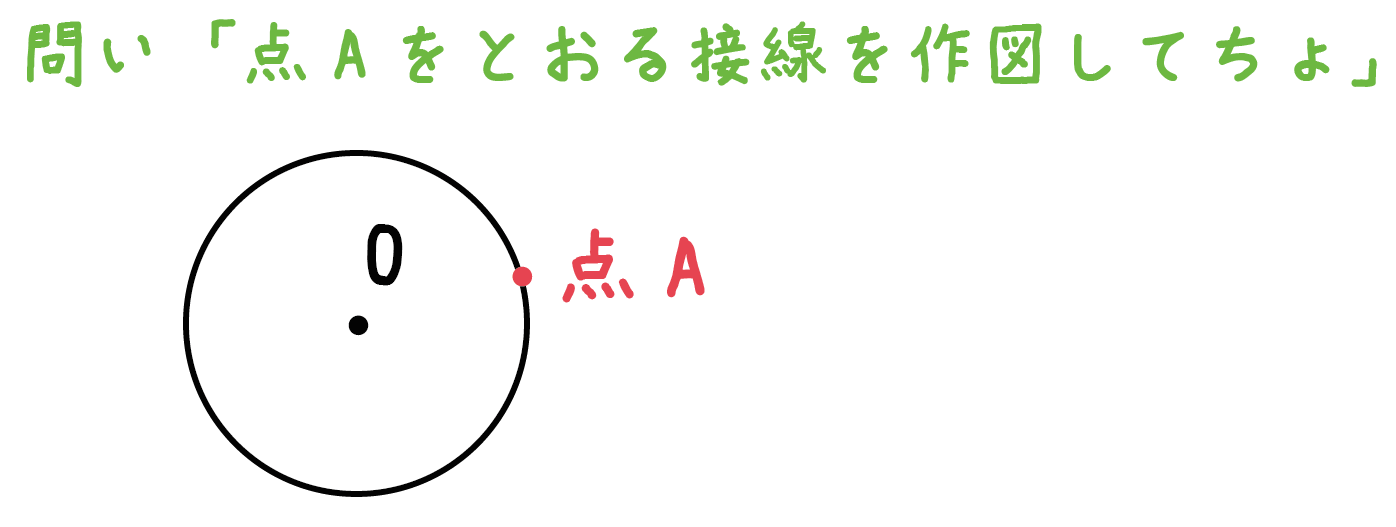
作図方法はたったの2ステップなんだ。

Step1. 「円の中心O」と「点A」をむすぶっ！

「円の中心」と「接線が通る線」で直線をかこう！

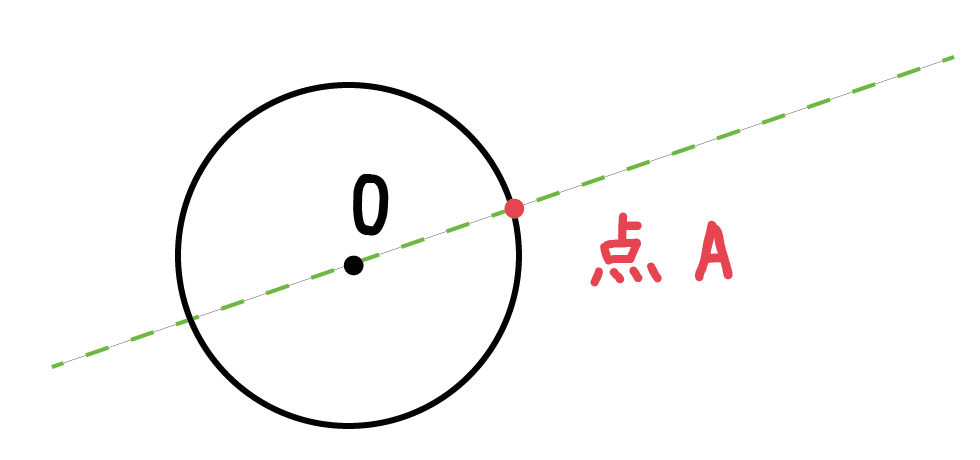
例題でいうと、「点O」と「点A」を定規でむすぶだけ。

線分じゃなくて直線でいいよー

Step2. 点Aをとおる「直線OAの垂線」を作図するっ！

さっきの直線の垂線を作図してみよう。

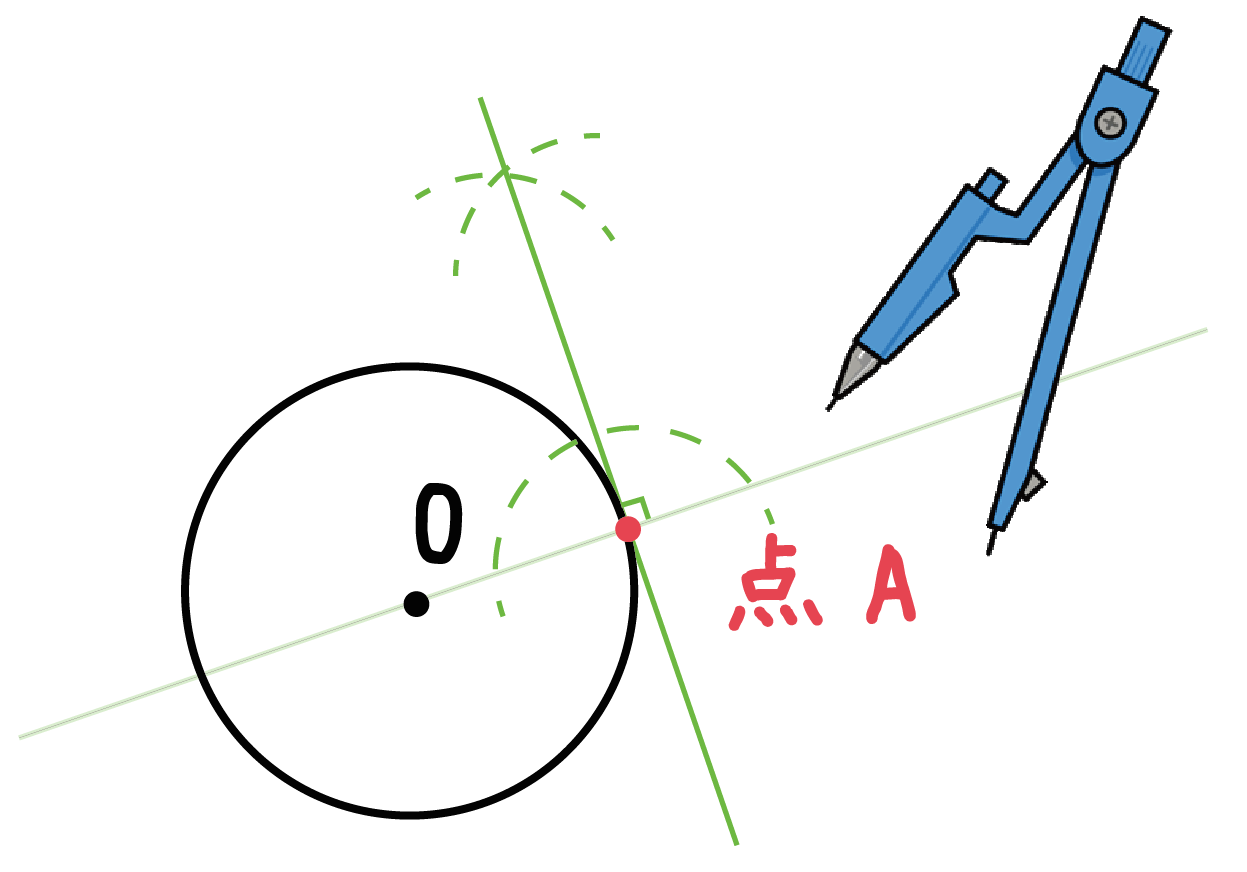
垂線の書き方を参考にして、「点Aをとおる直線OAの垂線」をかいてみよう。

コンパスをガンガン使っちゃってくれ^^

この垂線が「円Oの接線」だよ！

ってことは作図終了だ！！おめでとう^^

なぜ、垂線を作図するのかというと、

円の接線の性質のひとつに、

円の接線は、その接点を通る半径に垂直である

っていうものがあるからさ。

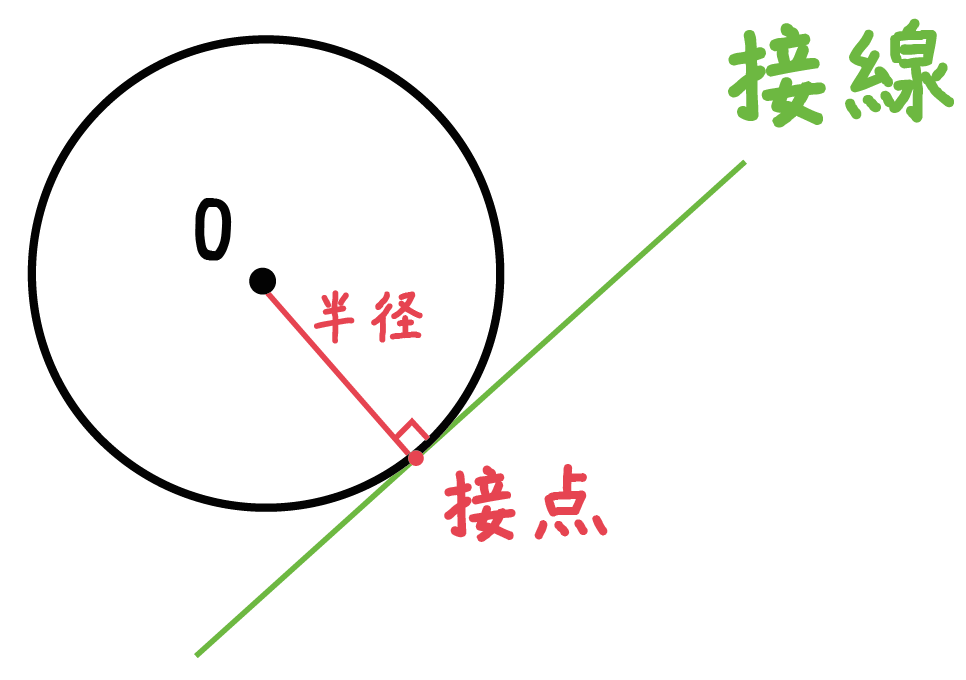
だから、円周上の点Aをとおる「線分OAの垂線」をひいてやれば、それは接線になるんだ。

「外部の点」をとおる接線の作図

つぎは2つ目の「外部の点をとおる作図方法」をみていこう。

例題をみながら解説していくよ。

例題

点Aをとおる円Oの接線を作図してください。

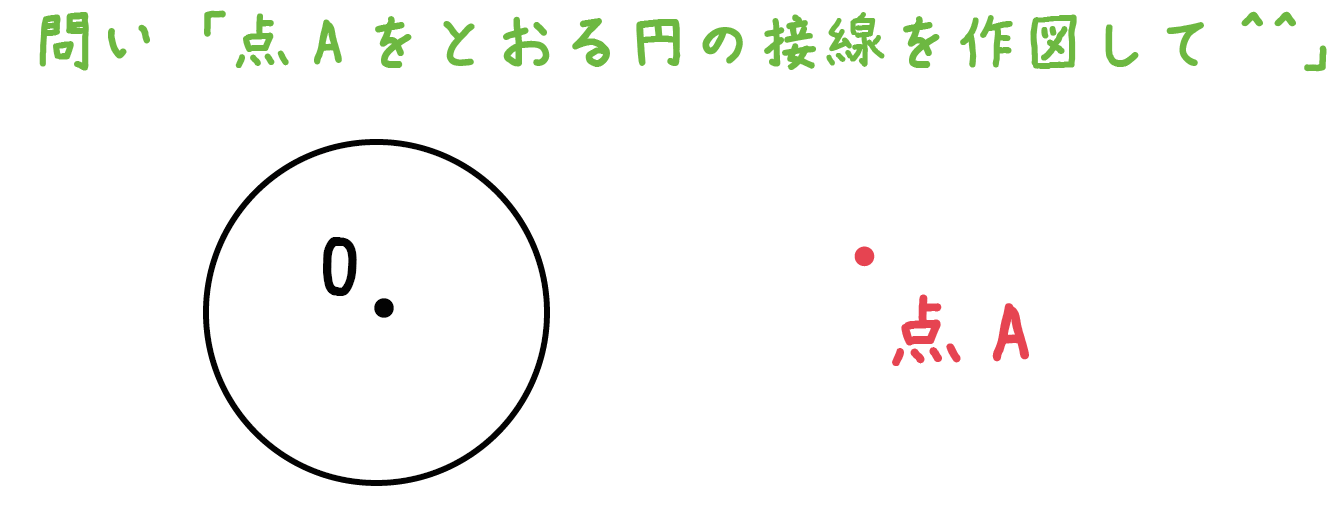
つぎの5ステップで作図できるよー

Step1.　「円の中心」と「外部の点」をむすぶ

「円の中心」と「外部の点」をむすんでみよう。

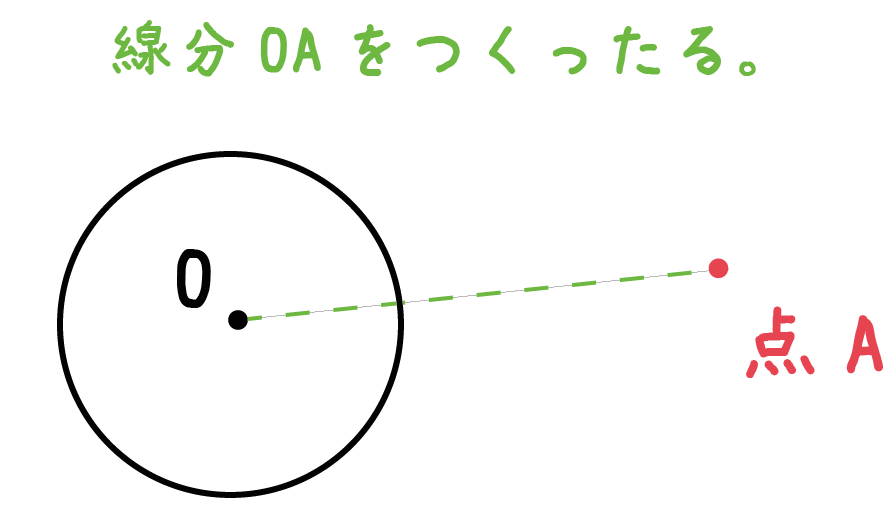
例題では、点Oと点Aだね。

こいつらを定規をつかってゴソっと結んでくれ！

Step2.　線分の垂直二等分線をかくっ！

「円の中心」と「外部の点」をむすんでできた線分があるでしょ？？

今度はそいつの「垂直二等分線」をかいてあげよう。

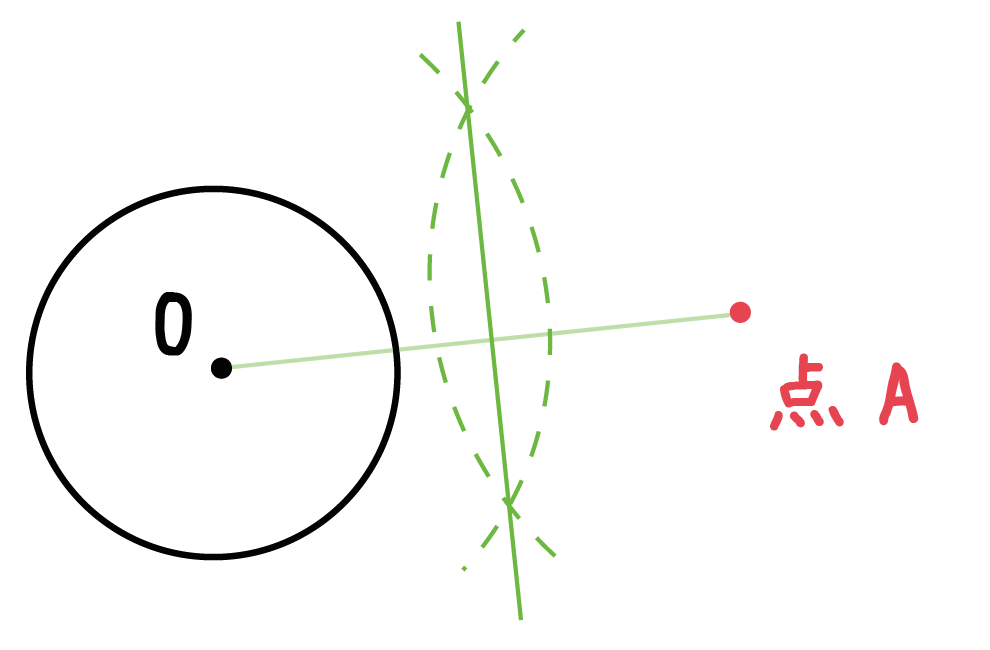
書き方を忘れたときは「垂直二等分線の作図」の記事を復習してみてね^^

Step3. 垂直二等分線と線分の交点「中点」をうつ！

垂直二等分線をかいたのは、

線分の中点をうつためだったんだ。

垂直二等分線は、線分を「垂直」に「二等分」する線だったよね。

ってことは、線分との交点は「中点」だ。

せっかくだから、この中点に名前をつけよう。

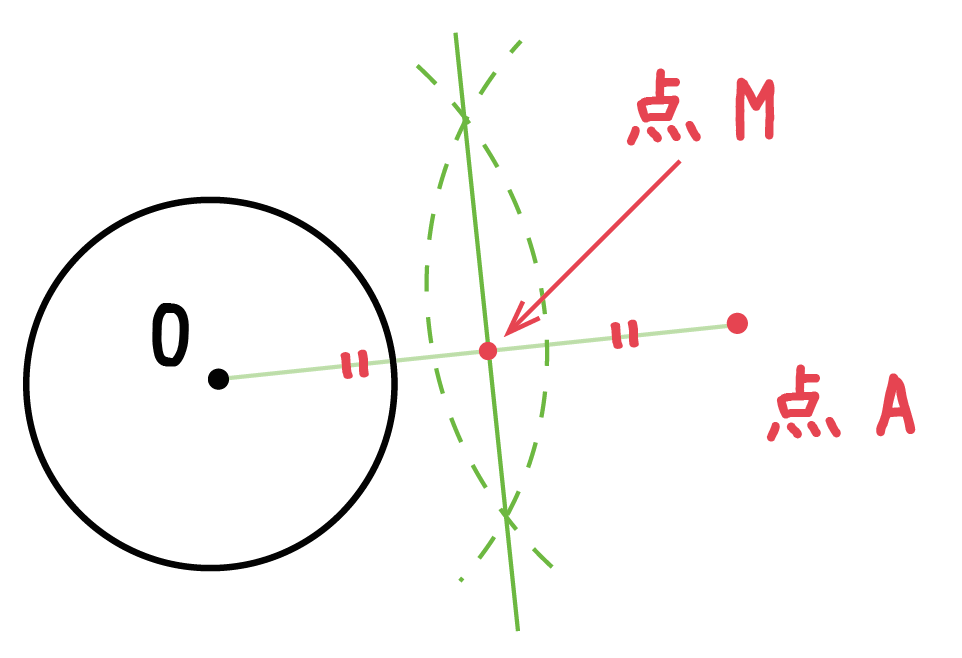
例題では「点M」とおてみたよ^^

Step 4.  「線分の中点」を中心とする円をかく！

「線分の中点」を中心に円をかいてみよう。

例題でいうと、Mを中心に円をかくってことだね。

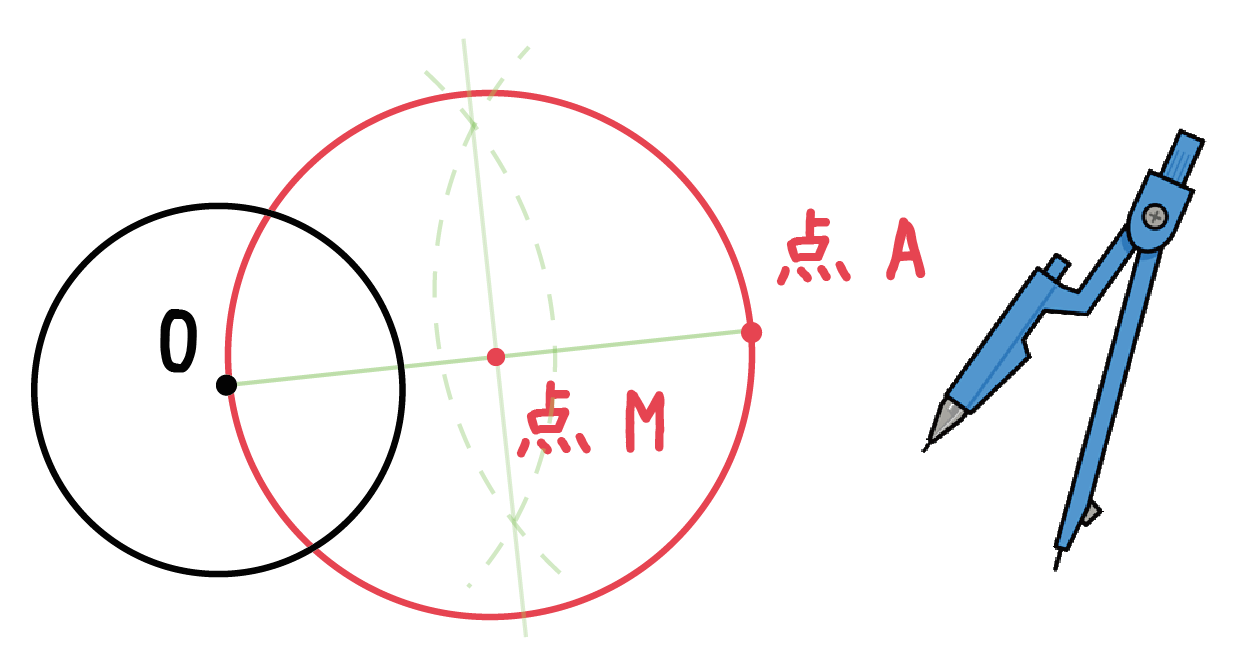
コンパスでキレイな円をかいてみてね^^

Step5.  「2つの円の交点」と「外部の点」をむすぶ！

「2つの円の交点」と「外部の点」をむすんであげよう。

それによって、できた直線が「円の接線」ってことになる。

例題をみてみよう。

円の交点を点P、Qとおこう。

そんで、こいつらを「外部の点A」とむすんであげればいいんだ。

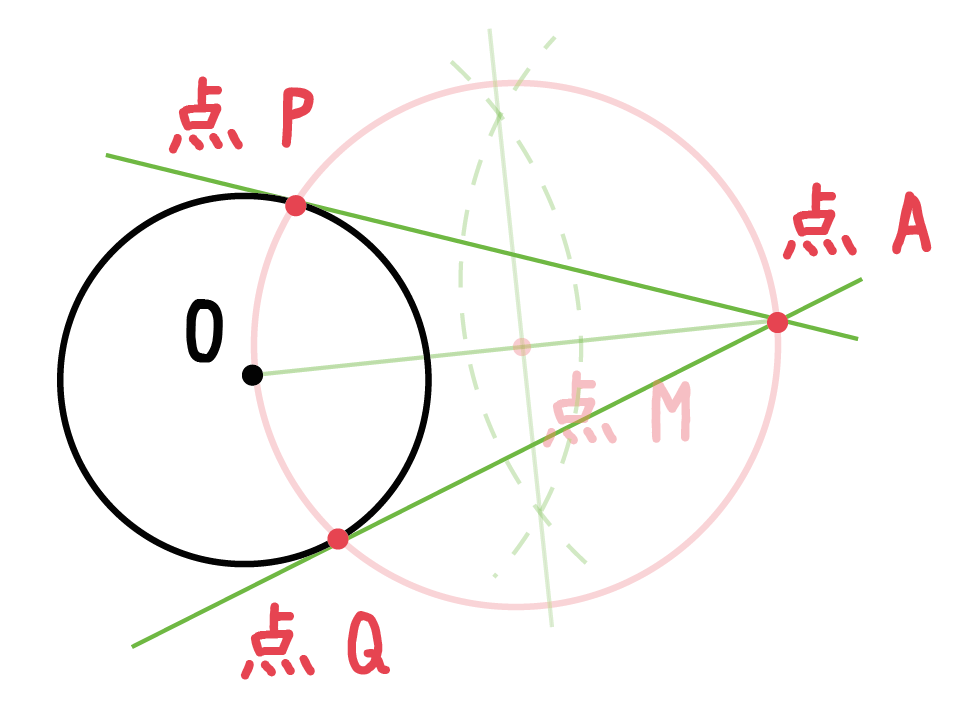
これによって、できた2つの「直線AP」と「AQ」が円Oの接線さ。

2本の接線が作図できることに注意してね^^

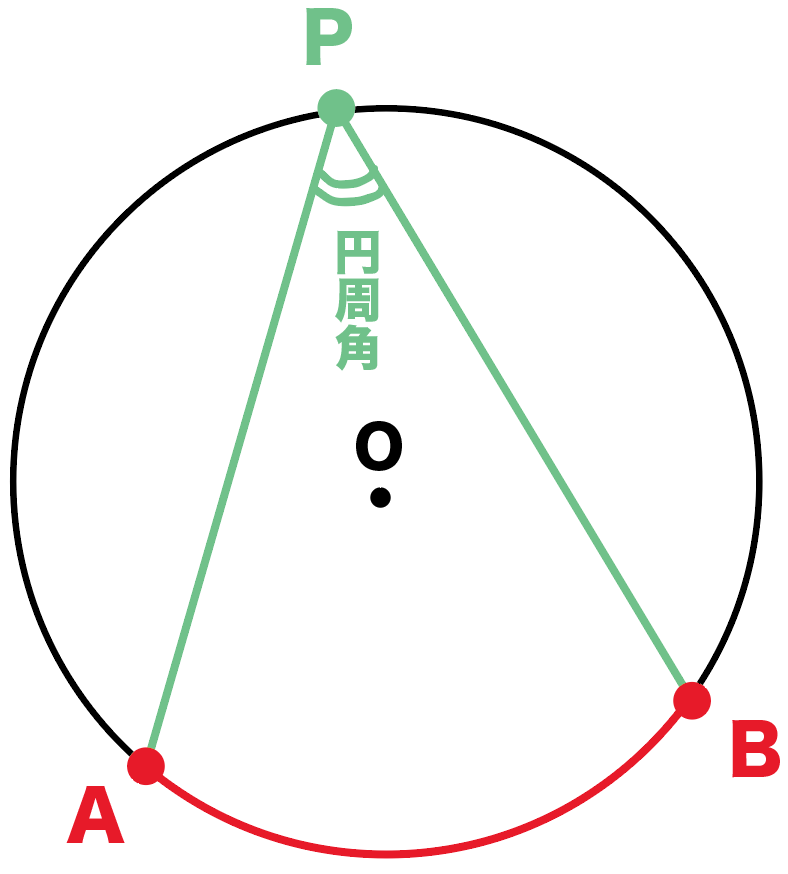
なぜこの作図方法で接線がかけるの？？

それじゃあ、なんで「円の接線」かけっちゃったんだろう？？

じつは、

直径に対する円周角は90°である

っていう円周角の性質を利用したからなんだ。

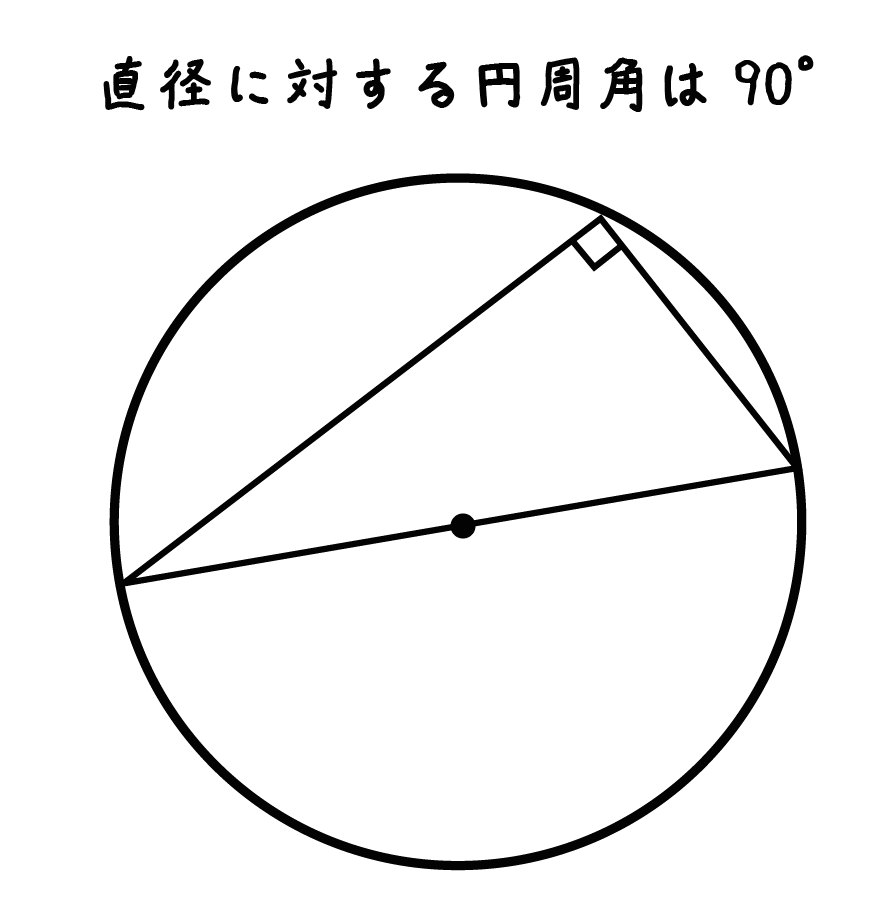
よって、

「角OPA」と「角OQA」が90°である

ってことが言えるんだ。

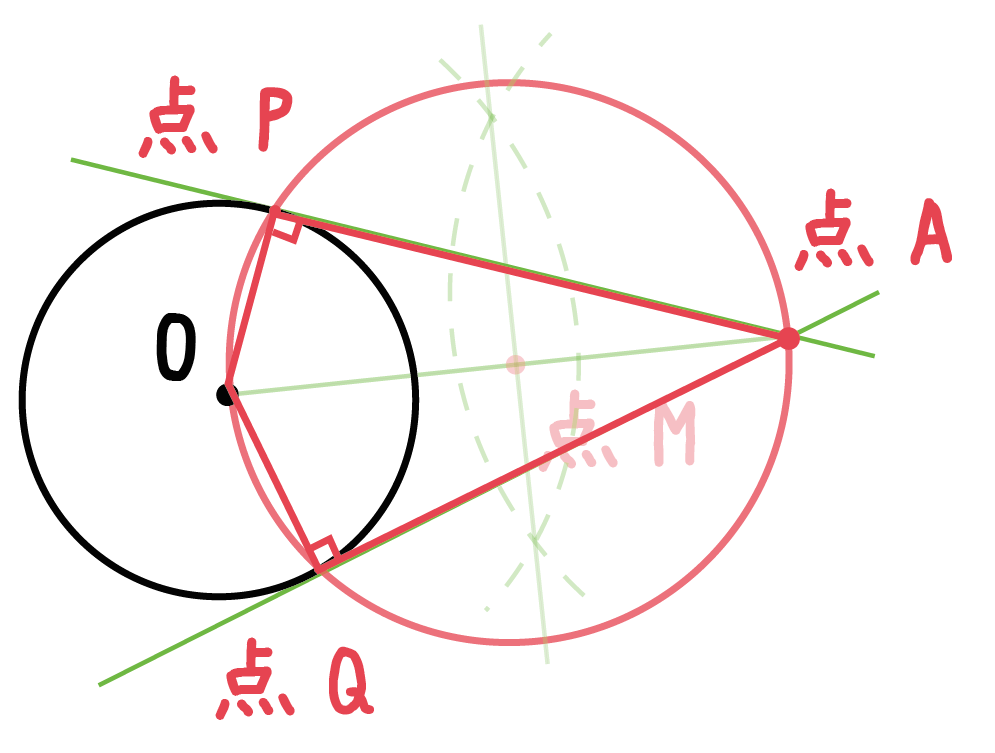
さっきの「円の接線の性質」、

円の接線は、その接点を通る半径に垂直である

をつかえば、線分PA、QAは円の接線ってことになるんだね。

これは中2数学でならう内容だから、今はまだわからなくても大丈夫だよー。

まとめ：円の接線の作図は2パターンしかない

2つの「円の接線の作図パターン」をおさえれば大丈夫。

作図問題がいつ出されてもダメージをうけないように、テスト前に練習してみてね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。