度数分布表からの平均値の求め方がわからん??
こんにちは!この記事をかいているKenだよ。山、みたいね。
平均値の求め方はわかってる。
だって、
「データの合計」を「データの個数」で割ればいいんでしょ??

ちょろいよ。
たとえば、A・B・C・D君のテストの平均値を求めてみよう。
かりに、4人の点数が、
- A君: 72点
- B君: 65点
- C君: 80点
- D君: 99点
だとするね。
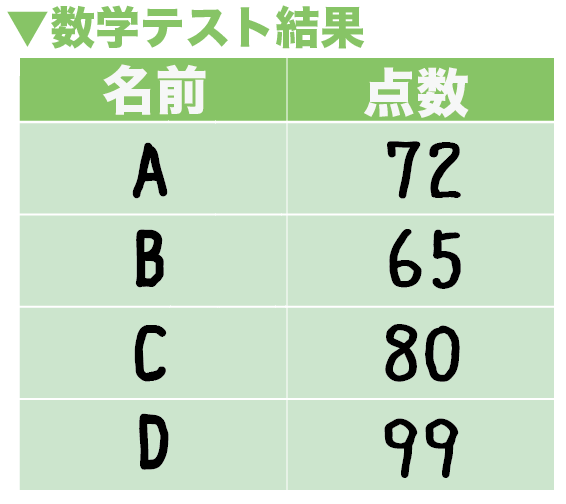
こいつらの平均点は、
(データの合計)÷(データの個数)
= (72 + 65 + 80 + 99)÷ 4
= 79
になる。
ぶっちゃけ、楽勝だね!
だけどさ、
度数分布表から平均を求めるとき
ってどうすればいいんだろ??
テストや宿題ででてくるのに、教科書にのってない。。
こいつは困ったね。
そこで今日は、
度数分布表からの平均値の求め方
を5ステップで解説してみたよ。
度数分布表からの平均値の求め方がわかる5ステップ
度数分布表から平均値を求めるときは、
つぎの公式をつかうよ。
「(階級値×度数)の合計」÷「度数の合計」

「階級値」と「度数」をかけたものをぜーんぶたして、
「度数の合計」でわればいいんだ。
えっ、言葉だけじゃよくわからん??
実際に例題をといてみよう!
例題
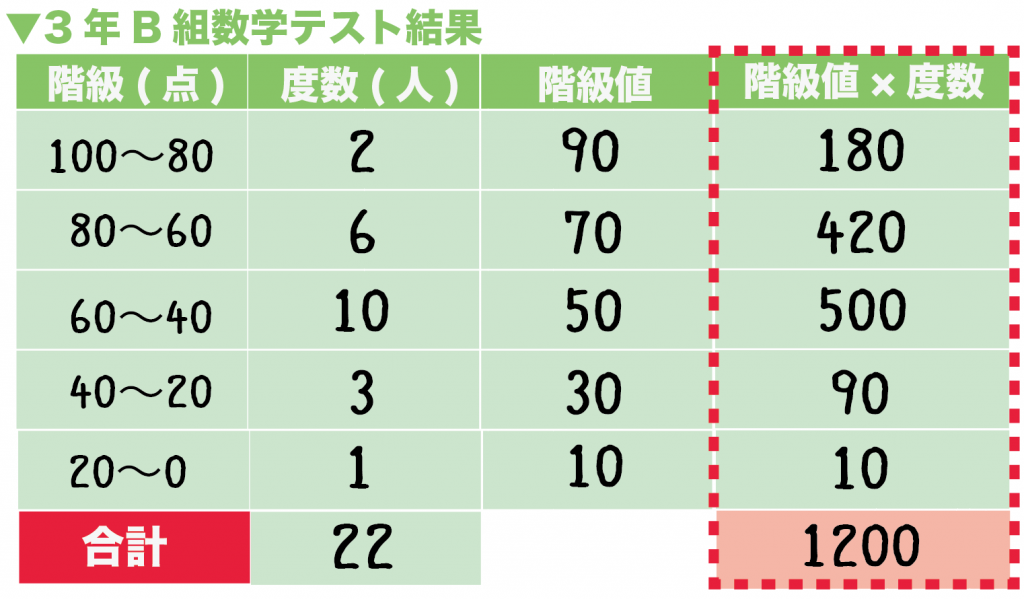
つぎの度数分布表は3年B組の期末テストの点数の分布をあらわしたものです。この度数分布表から平均値を求めなさい。
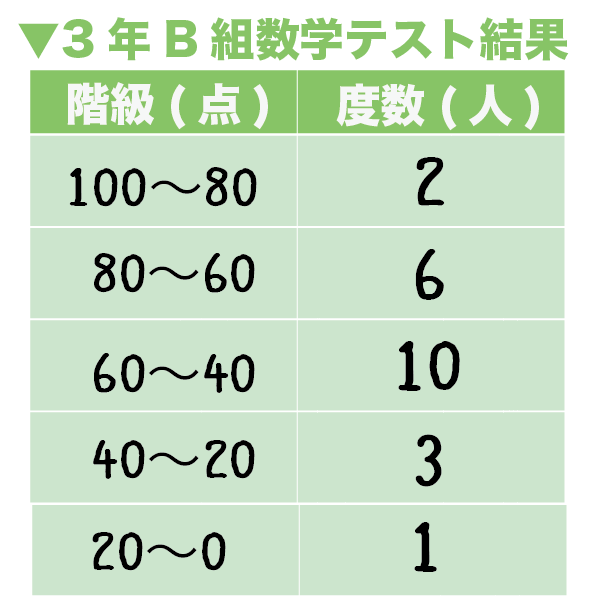
つぎの5ステップで計算できちゃうよ。
- 階級値をだす
- 「階級値×度数」を計算する
- 度数の合計をだす
- 「階級値×度数」の合計をだす
- 公式をつかう
Step1. 階級値をだす!
各階級の「階級値」を計算してみよう!
階級値の求め方は、
(階級の端+階級の端)÷ 2
だったよね??

たとえば、階級が「100~80」だったら、
(100 + 80 ) ÷ 2
= 90
になるってわけ。
こんな感じで、階級の端っこの平均をだせばいいんだ。
例題の階級値をぜーんぶだしてやると、
- 階級 100 ~ 80 : 階級値 90
- 階級 80 ~ 60: 階級値 70
- 階級60 ~ 40: 階級値 50
- 階級40 ~ 20 : 階級値 30
- 階級20 ~ 0 : 階級値 10
になるね。
これが第1ステップ!!
Step2. 「階級値×度数」を計算する!
つぎはさっき計算した、
階級値
と
度数
をかけてみよう。

例題で「階級値×度数」を計算してみると、
- 階級 100 ~ 80 : 90 ×2 = 180
- 階級 80 ~ 60: 70 × 6 = 420
- 階級60 ~ 40: 50 × 10 = 500
- 階級40 ~ 20 : 30 × 3 = 90
- 階級20 ~ 0 : 10 × 1 = 10
になるね。

慎重にかけ算をしてみよう!!
Step3. 「度数」の合計をだす
おつぎは、
度数の合計
を計算しよう。
ぜーんぶの階級の「度数」をたせばいいのさ。
例題でいうと、各階級の度数は、
- 階級 100 ~ 80 : 2
- 階級 80 ~ 60: 6
- 階級60 ~ 40: 10
- 階級40 ~ 20 : 3
- 階級20 ~ 0 : 1
だったね??
こいつらをぜんぶ足してやると、
2 + 6 + 10 + 3 + 1
= 22
になる!
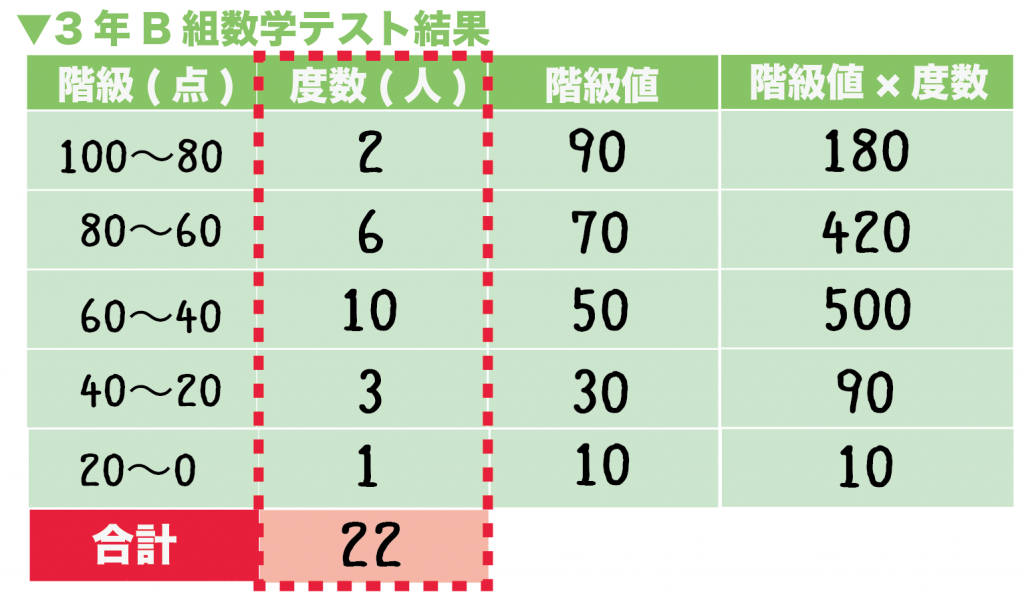
Step4. 「階級値×度数」をたしたる!
「階級値×度数」の合計もだしてみよう!
ぜーんぶの階級の「階級値×度数」をたせばいいんだ。
例題の「階級値×度数」は、
- 階級 100 ~ 80 : 180
- 階級 80 ~ 60: 420
- 階級60 ~ 40: 500
- 階級40 ~ 20 : 90
- 階級20 ~ 0 : 10
だったよね??
こいつをぜんぶたしてやると、
180 + 420 + 500 + 90 + 10
= 1200
になるね。
Step5. 公式をつかう!
最後に平均値の公式をつかおう!
度数分布表から平均値を求める公式は、
「(階級値×度数)の合計」÷「度数の合計」

だったね??
Step4まででそろえた、
- (階級値×度数)の合計
- 度数の合計
を公式にぶちこんでみよう。
例題では、
- (階級値×度数)の合計:1200
- 度数の合計: 22
を公式にいれて計算してやると、
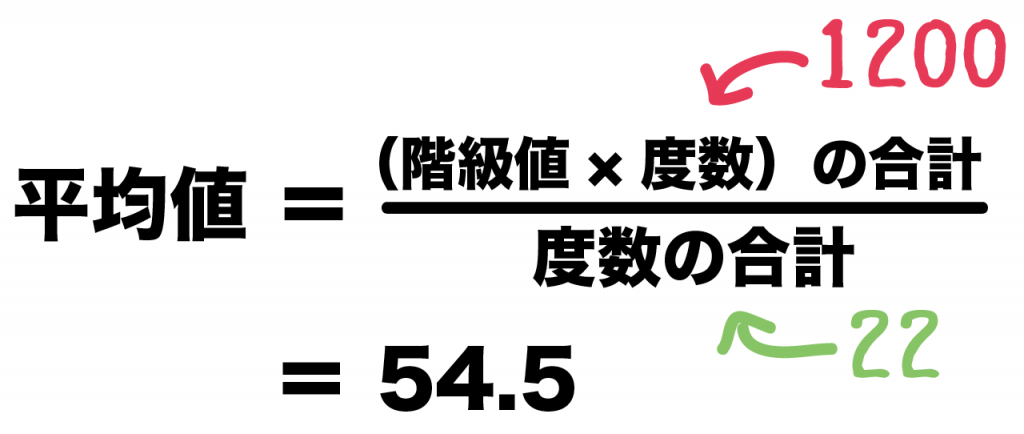
(階級値×度数の合計)÷(度数の合計)
= 1200 ÷ 22
= 54.5※小数点第二位を四捨五入
になる!
おめでとう!
どんな度数分布表からも平均値を求められるね^^
まとめ:度数分布表から平均値を求め方は足し算・かけ算・割り算をつかえ!
度数分布表から平均値をだすのはむずい。
だけど、ふたをあけてみると案外簡単。
使ってるのは、
- 足し算
- かけ算
- 割り算
の3つだからね。
求め方さえおぼえちまえば、計算は簡単なんだ。
度数分布表からガンガン平均値を求めていこう!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。














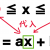












グラフや表からの平均値や中央値のもとめ方がわかりません。どうやってやるのですか?
>2(x+4)^2=5
両辺を2で割って両辺にルートをつけよう!
中央値を一発で求めるには?
>中央値を一発で求めるには?
中央値は度数の大きい順に並び替えるのが一番かな。
中央値の求め方を読んでみてー
度数が分からない時は、どうすればいいですか?
>度数が分からない時は、どうすればいいですか?
度数は階級に当てはまるデータの個数だ。
たとえば、身長160~170cmという階級があっととして、クラスにその身長に当てはまる人が100人いたら度数は100だ
この問題よろしくお願いします
35+19+25+28+21+31+16+a
+23+52-a
平均値とaの値を教えてください
分散は28.6
aは平均値以下です
度数が出ていない階級があって、平均値が出ている場合、どのようにして度数を求めたら良いのですか?
>度数が出ていない階級があって、平均値が出ている場合、どのようにして度数を求めたら良いのですか?
求めたい度数を文字でおいて(例えばx)、
平均値を求める公式に入れて度数を方程式で求めてみよう!
わかりやすすぎ!
ありがとうございます
ステップ5で、割るときいつまでも割りきれない場合ってどうすればいいですか?小数第何位~とかの指示がありません!
学校でもらったプリントなんですけど….
>ステップ5で、割るときいつまでも割りきれない場合ってどうすればいいですか?小数第何位~とかの指示がありません!
そういう時は自分で小数何位まで四捨五入するか決めちゃっていいよ!
答えのところに(〜位で四捨五入した)とか書いておけばオッケー
平均値が少数になった場合、四捨五入しなければ間違いですか?
(平均値は少数第一位で割りきれました)
>平均値が少数になった場合、四捨五入しなければ間違いですか?
(平均値は少数第一位で割りきれました)
小数が無限に続きそうだったらしたほうがいいね。
問題に四捨五入の桁数が記載されていなかったら自分で決めていいと思うよ
ここの部分がすごく分からなかったのですが
すごくわかりやすい回答でした!!
わかってスッキリしました!!
ありがとうございます
ありがとう!!
わかりやすくて助かりました!!
ありがとうございます!
なるほど!。分かりやすくて、楽しい説明ですね!。ありがとうございます
相対度数の求め方
分かりやすいです!
ありがとうございます
すみません!
階級値の意味があまりよく分かちませんでした。
階級値は何を求めているんですか?
また、階級値と度数をかけたら何がわかるんですか?
階級値は「ある階級がどこらへんのデータの範囲を扱えっているのか?」という目安かな。
ラベルみたいなもんだ
階級値と度数をかけたら、そのラベルをつけたデータの数がどれくらいあるのか、というデータの量がわかるね
変域の求め方を分かりやすくお願いしたいですー
一次関数の変域の解き方を読んでみて!
階級
30-35
35-40
40-45
45-50
50-55の範囲を求めろの問題の解き方を教えてください
まずはそれぞれの階級の階級値を計算してみよう
すごいわかりやすいです。これでテストもイチコロです。
相対度数の出し方教えてください。
ありがとうございました!
凄く分かりやすかったです。
これで、問題もすらすら解けそうです!
オール5を取るのはどうすればいいですか?
中央値の求め方(6年生)の分が知りたいのですが、調べても基本のやつしか出てこなくて、、標準のやつが出来れば知りたいです…っ!!
標準の平均値の求め方はここに書いておきました!
中央値はこちらに!
例えば -18+12+4-12-6+2÷6はどうすればいいですか?(小6)
この度数分布表からの平均値の最も大きい値ってどうやって求めたら良いんでしょうか?
度数分布表から出す平均と生データから出す平均が異なっているのはなぜですか。