【平方根の計算】ルートを簡単にする方法がわかる3つのステップ

平方根（ルート）を簡単にする方法ってなに？？

こんにちは！この記事をかいてるKenだよ。朗読をはじめたね。

平方根の計算でよくつかうのは、

ルートを簡単にする方法

だ。

ぶっちゃけ簡単にしなくてもいいんだけど、計算しやすくなるんだ。

しかも、先生によってはルートが簡単じゃないと×にするから要注意。

そこで今日は、

平方根（ルート）を簡単にする方法

を解説していくよ。

よかったら参考にしてみて。

= もくじ =

1. ルートを簡単にするってなに？？
2. ルートを簡単にする方法

ルートを簡単にするとは・・・！？

「ルートを簡単にする」とはずばり、

ルートの中身から整数を取り出すこと

なんだ。

たとえば、

√（aの2乗×b）

があったとしよう。

ルートを簡単にするってようは、

中身の「aの2乗」をルートの外に出すことなんだ。

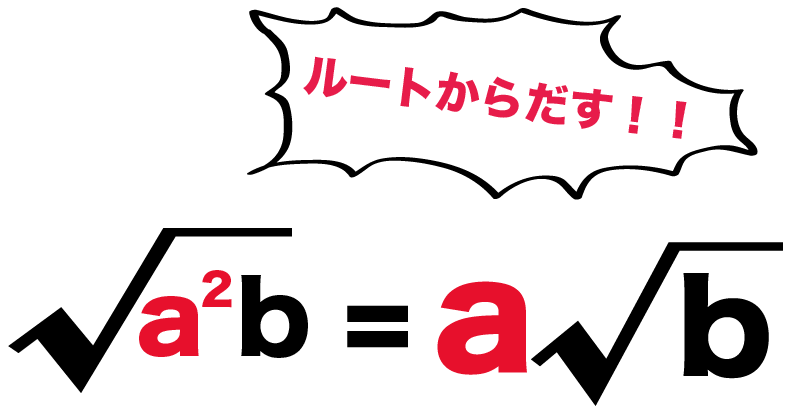
aの2乗をルートの外にだしてやると、

√（aの2乗×b）= a√b

になるね。

なぜなら、

√（aの2乗×b）
= √（aの2乗）× √b
= a×√b
= a√b

になるからさ。

ルートを簡単にする方法の3ステップ

ルートを簡単にする方法はたったの3ステップ。

1. ルートの中を素因数分解
2. 「2乗」の因数をみつける
3. ルートの外にだす

例題をいっしょにといてみよう。

例題

つぎの平方根たちの中身をできるだけ簡単にしてください。

(1 ) ルート12　(2) ルート112 　(3)ルート180

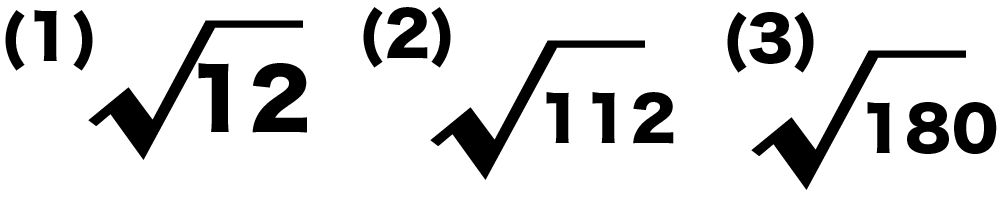
Step1. ルートの中身を素因数分解

ルートの中身を素因数分解してみよう。

えっ。

素因数分解なんて忘れたって？！

そういうときは、素因数分解のやり方をよんでみて^^

例題も素因数分解してみよう。

• ルート12
• ルート112
• ルート180

の根号のなかにはいってるのは、

• 12
• 112
• 180

たちだね。

こいつらを素因数分解してやると、

• 12  = 「2の2乗 × 3」
• 112 = 「2の4乗×7」
• 180 = 「2の2乗×3の2乗×5」

になる。

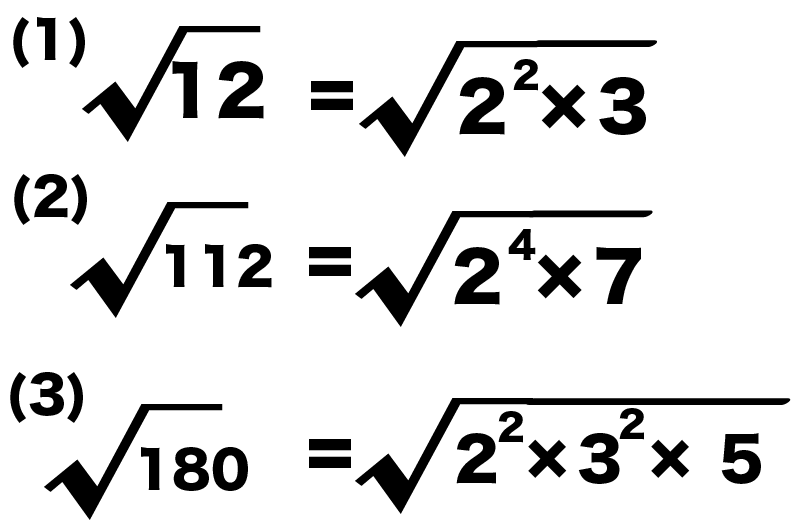
Step2. 「2乗」の因数をみつける！

ルートの中から、

2乗になっている因数

をみつけよう。

例題の平方根たちをみてみると、

• 12  = 「2の2乗 × 3」
• 112 = 「2の4乗×7」= 「4の2乗×7」
• 180 = 「2の2乗×3の2乗×5」

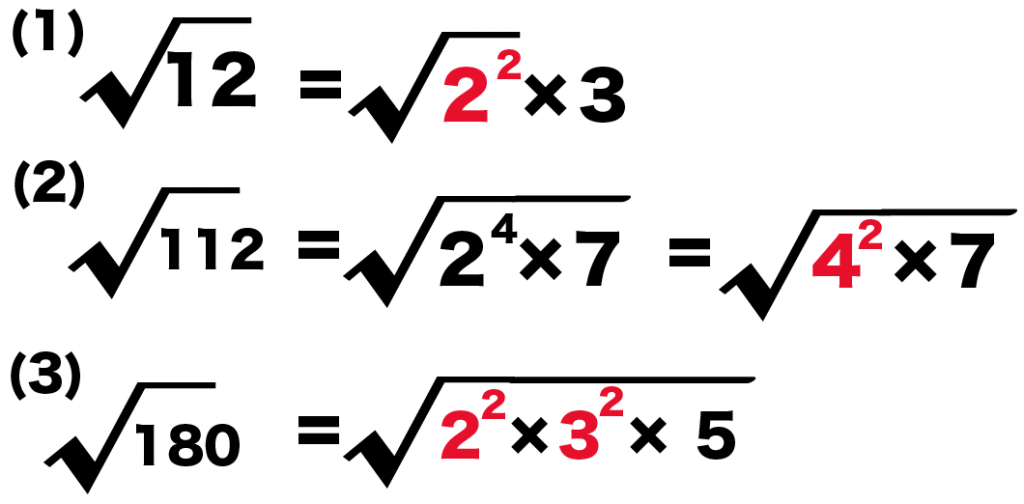
ってかんじで、ちらほらと2乗の因数がみつかったね。

えっ。

112みたいに4乗になっている因数がある？？

そういうときは、それを「2乗した数」の2乗になっていると解釈しよう。

Step3. ルートの外にだす！

最後に、2乗の因数を√の外にだそう。

例題でも、2乗になってる因数をとりだすと、

• √12  = √ ( 2の2乗 × 3) = 2√3
• √112  = √( 4の2乗×7 ) = 4√7
• √180 =  √( 2の2乗×3の2乗×5 ) = 2×3√5 = 6√5

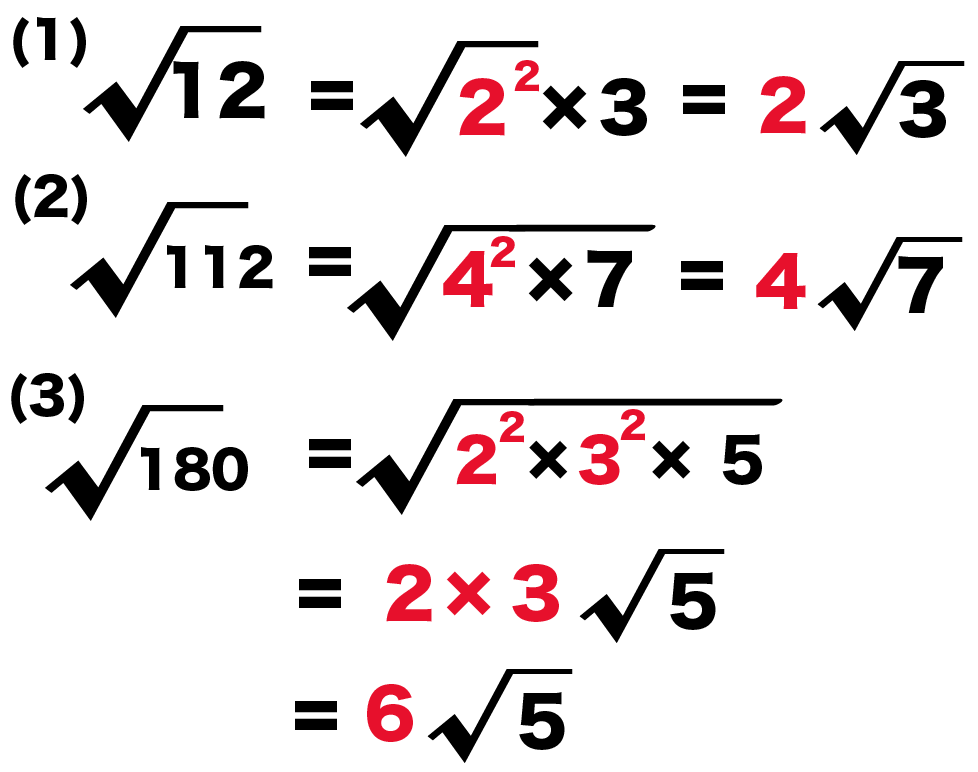
になるね！

まとめ：平方根を簡単にするために素因数分解！

平方根を簡単にする方法はどうだった？？

1. 素因数分解する
2. 「2乗」の因数をみつける
3. ルートの外にだす

の3ステップで攻略できちゃうよ。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。