平方根(ルート)の掛け算のやり方を知りたい!
こんにちは!この記事をかいているKenだよ。海につかりたいね。
平方根の計算にはいろいろある。
それこそ、
足し算、引き算、割り算、、、、、とか、もう、数えきれない。
そんななかに、
ルートの掛け算の計算
がある。
ルートの中身を掛け算するだけ
だったよね??
そんなむずくなさそう。
だけどね、実際の計算問題だとそうはいかない。
そんなに世間は甘くないんだ。
そこで今日は、平方根の掛け算の計算方法を紹介していくよ。
平方根(ルート)の掛け算がわかる5ステップ
平方根の掛け算は5ステップで計算できるよ。
- ルートを簡単にする
- 整数同士をかける
- 平方根同士をかける
- くっつける
- ふたたびルートを簡単にする
えっ。5ステップもあるからダルいって!??
ノンノン。
複雑にみえるけど、一瞬で計算できる。
安心してくれ。
例題をといていこう。
例題
つぎの平方根の計算をしてください。
(1) √12 × √32 (2) √7 × √21 (3) √48 × √27

Step1. 平方根を簡単にする
平方根を簡単にしてみよう。
「ルートを簡単にする」ってようは、
2乗になってる因数を取り出す
ってことだ。
⇒ くわしくは「平方根を簡単にする方法」をよんでみて
例として、(1)をみてみよう。
(1) √12 × √32
√12と√32をそれぞれ簡単にしてやると、
- √12 = 2√3
- √32 = 4√2
になる。
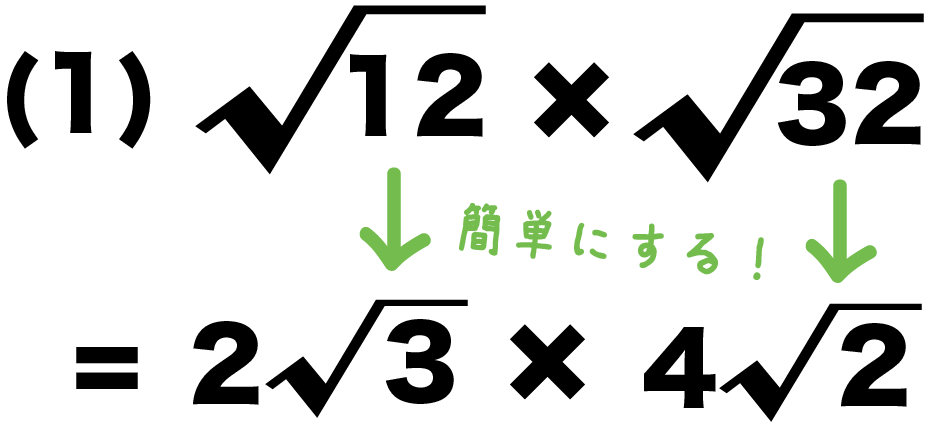
つぎは(2)の掛け算だ。
(2) √7 × √21
この平方根たちは簡単にできないね。
なぜなら、中身に2乗の因数がないからさ。

(3)も簡単にしてやると、
(3) √48 × √27
= 4√3 × 3√3
になるね!

Step2. ルート前の整数をかける
つぎは、整数の掛け算をしよう。
ルートはいったん無視していいや。
例題の(1)の計算でいうと、
(1) √12 × √32
= 2√3 × 4√2
だったよね??
だから、整数の掛け算は、
2×4
= 8
になるね。

おなじように、(3)でも計算すると、

4×3
= 12
になるね!
ちなみに、(2)は整数がないからステイね。
Step3. 平方根部分を計算する
つぎは、平方根の掛け算をするよ。
ルートを1つにして中身だけ計算しちゃう
だったよね??

例題でもおなじさ。
(1) √12 × √32
= 2√3 × 4√2
の平方根部分の掛け算は、
√3 × √2
= √6
になるね!

例の(2)もおなじ。
平方根の掛け算の基本をつかって計算すると、
√7×√21
= √147
になるね!

例題の(3)の、
√48 × √27
= 4√3 × 3√3
でもおなじさ。
平方根の掛け算をしてやると、
√3×√3
= 3
になるね。

Step4. くっつける
さっき計算した、
- 整数部分
- ルート部分
をくっつけてやろう。
ピタっとくっつけるだけでいいんだ^^

例題の(1)だったら、
(1) √12 × √32
= 2√3 × 4√2
= 8√6
になるね。

(2)は平方根だけの掛け算だからステイ。

(3)の平方根の計算は、
√48 × √27
= 4√3 × 3√3
= 12×3
= 36
になるね!

Step5. ルートを簡単にする
最後に、ルートをもっと簡単にできるか挑戦。
ルートの中身はいちばん簡単にすべきだからね。
例題の計算をみてみると・・・
・・・ん!?
(2)のルートはもっと簡単にできそうじゃないか??
中身の147を素因数分解すると、
147 = 3×7の2乗
になってる。
因数の7が2乗になってるじゃん??

最終的に、(2)の計算問題は、
√7×√21
= √147
= 7√3
になるね。

こんなかんじで、
ルートをもう一度簡単にできるか
チェックしてみよう!
まとめ:平方根の掛け算は簡単にしてから!
平方根の掛け算のコツは、
ルートを簡単にして、整数と平方根をわけるってこと。
そのほうが計算が楽。
じゃんじゃんルートの掛け算していこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







平方根の利用はどうやるんですか?教えて下さい。
どういう問題??
x=ルート7+ルート2、y=ルート7-ルート2のときの(x+y)の2乗の値の求め方を教えてください。
>x=ルート7+ルート2、y=ルート7-ルート2のときの(x+y)の2乗の値の求め方
まずは(x+y)の2乗を展開する前に、xとyを代入してみよう。
いい感じに、ルート2が消えるはずなんだよね
ルート3×ルート27はどうして9になるんですか?
>ルート3×ルート27はどうして9になるんですか?
ルート27を簡単にしてみよう
6√75は簡単に出来ますか?
>6√75は簡単に出来ますか?
できそうだね。
75を素因数分解してみて
-8と-√65ではどちらが大きいんですか?
ルートが入った式の展開はどうやれば良いですか?
例(√3-1)(√3+2)
(√3-√7)の2乗
(√5+√2)(√5-√2)など…
2√3-√48が分かんないです。
>-8と-√65ではどちらが大きいんですか?
どっちもルートにすると大小を比較できるよ。
-8をルートの形にしてみよう。
詳しくは「ルートの大小を比較する方法」を読んでみて
>ルートが入った式の展開はどうやれば良いですか?
ルートが入っていない時と同じだよ!
乗法の公式を使って式を展開していこう!
>2√3-√48が分かんないです。
まずはルート48を簡単にしてみよう。
48を素因数分解して、2乗を探してみて!
整数×ルート=整数√数字
にすると不正解ですか?
>整数×ルート=整数√数字
にすると不正解ですか?
いや、いいと思うよ
(2ルート6➕1)2乗
整数×ルートって、どうやって計算するんですか?
ちなみに、選択肢は、
1、13+2ルート6
2、13+4ルート6
3、25+2ルート6
4、25+4ルート6
です。教えてください!!m(_ _)m
>(2ルート6➕1)2乗
これは乗法の公式の中の「平方の公式」で展開してみよう。
ルートが入っていようがなかろうが、解き方は同じ。
(x+1)2乗の展開と一緒の解き方で解いてみよう
ルートの計算式の解き方を教えてください❗
>ルートの計算式の解き方を教えてください❗
ルートの計算のコツを読んでみて
√18×√28って3√2と2√7になりますよね?
その後の計算ってそれぞれ掛けて6√14で合ってますか?
(文章力なくてごめんなさい)
>√18×√28って3√2と2√7になりますよね?
その後の計算ってそれぞれ掛けて6√14で合ってますか?
あってるよ!
今回みたいにルートを簡単にしてから計算すると楽になるね!
5√5×5って、5x×5と同じ方法でやればいいですか?
>5√5×5って、5x×5と同じ方法でやればいいですか?
そうだね。
整数は整数、文字は文字、ルートはルート同士で掛け算するんだ
√15(3√5-2√3)の解き方を教えて下さい。
√48÷√6
>√15(3√5-2√3)
分配法則で()を展開してみよう。
あとはルートを簡単にすればいいかな
>√48÷√6
ルートの割り算の場合、ルートの中身をそのまま割り算すればいいね!
(1+2√3-√2)+(2√3-√2)の二乗のしかたがわからないです。。!
詳しく教えていただけますか!?
2√10×4√5ってどーやってやるんですか?
>(1+2√3-√2)+(2√3-√2)の二乗
最初に平方の公式で(2√3-√2)の二乗を展開してみよう。
最後にルートの足し算・引き算で計算だ
>2√10×4√5ってどーやってやるんですか?
整数は整数、ルートはルートで計算してみるといいよ。
ルートの掛け算はルートの中身同士をかければいいからね!
√2×5と√2×√5って同じ意味ですか?
>√2×5と√2×√5って同じ意味ですか?
√(2×5)と√2×√5なら同じかな!
もし5がルートの外にある整数だったら、
√2×5= 5√2になって同じ意味じゃなくなるよ
(√3+2√2)(√3+√2)
>(√3+2√2)(√3+√2)
これは乗法の公式で展開してみよう!
√3-3²+6×√3-3はどうやって解いたら良いですか?
>√3-3²+6×√3-3
指数の計算、掛け算、足し算引き算、
という順番で計算してみよう
√87√7という問題の解き方がわかりません
教えてください
9√2=1/2×3√6×х の解説お願いします
>√87√7という問題の解き方
ルートの掛け算は、ルートの中身同士をかけてやるといいよ
>9√2=1/2×3√6×х
xの前の係数で両辺を割って右辺をxだけにしよう。
あとはルートの割り算で約分したり有理化したりするね
√3✖︎1は、いくつになりますか?
質問です
√10-2.3乗×√10-9.7乗のやり方を教えてください。
>√3✖︎1は、いくつになりますか?
普通の掛け算と同じで1をかけても変わらないね!
>√10-2.3乗×√10-9.7乗
√10という共通因数でくくってみよう!計算が楽になるはずだ
朝テストで出題された問題なのですが、
4-2√3分の√6はどうやって計算したら良いでしょうか、。
答えがマイナスになってしまうのですがあってますでしょうか、、
>4-2√3分の√6
有理化する問題かな?
4が分母に含まれるとすると、
4+2√3 を分母と分子にかけてみよう
2×√6はなんですか
>2×√6はなんですか
ルートの計算は文字式と同じ。
×をなくしてみて
2√27×√12はなんですか?
>2√27×√12はなんですか?
まずはルートを簡単にするといいよ!
あとは整数とルートを別々に計算してやればいい
3√12−√3分の27ってどんな答えになりますか?
>3√12−√3分の27ってどんな答えになりますか?
3√12のルートを簡単にして、
−√3分の27の分母を有理化してみよう!
なんで簡単にすると12が3になったり、32が2になったりするんですか…?
よくわかんないです…
>なんで簡単にすると12が3になったり、32が2になったりするんですか…?
よくわかんないです…
これはルートを簡単にしてるんだね。
12を素因数分解してみると、
12 = 2 x 2 x 3
になるから、2の2乗が含まれていることがわかる。こいつをルートの外に出すと、ルートの中身が3になるのね
(4√3-√2)(5√3+√2)
こういう問題ってどうやって解けばいいんですか?
>(4√3-√2)(5√3+√2)
分配法則で()をはずそう!
あとはいつも通りルートの足し算を計算すればいいね
(5-2ルート3)×3乗
の解き方教えてください
>(5-2ルート3)×3乗
まずは(5-2ルート3)2乗を平方の公式で計算して
そいつに分配法則で(5-2ルート3)をかけてやるといいよ〜
30000をルートに変換するとどうなりますか
100の2乗が含まれているから100をルートの外に出せそうだね
(2√5+3√3)×5の答えを教えてください
これは分配法則を使って展開してみよう!
(2+√2)/(√2+1)=√2の意味が分からないので解説していただけませんか?
もともとは分数でした。
これは乗法の公式を使ってるな!
(x+a)(x+b)の展開公式だ
2ルート7+5ルート7の答えを教えて下さい。
ルートの前についている数字を足して最後にルート7をつけてやるといいな
√3(√2-1)²は、どうやってやるのですか?
まずは平方の公式で後ろの2乗を展開した方がいいね!
2√116×2 +80=110.46になるのでしょうか?
2√139×2 +80=の回答はどうなるのでしょう?
2√116×2+80=110.46になるの?
2√139×2+80=どうなるの?かを教えて下さい
2√139×2 +80=の回答を教えて下さい
連立不等式が入った平方根の計算なんですけど
√(3)x+6だいなりいこーる9
{
-2x+√(2)だいなりいこーる-1
ってどう解くんですか
(2)の問題は、先に√21を√3×√7にしてから計算する方法を教えるべきではないでしょうか?
ルート80×ルート15
るーとのときかたをおしえてください
めちゃくちゃわかりやすいです。
めちゃくちゃファンです。数学伸びてきました。数検に向けて頑張ります。これからもよろしくお願いします。
a<0,b0なので√abはあると思うのですが、右辺の√aと√bはこの場合何者なんですか?
ルート20÷ルート2x10=?