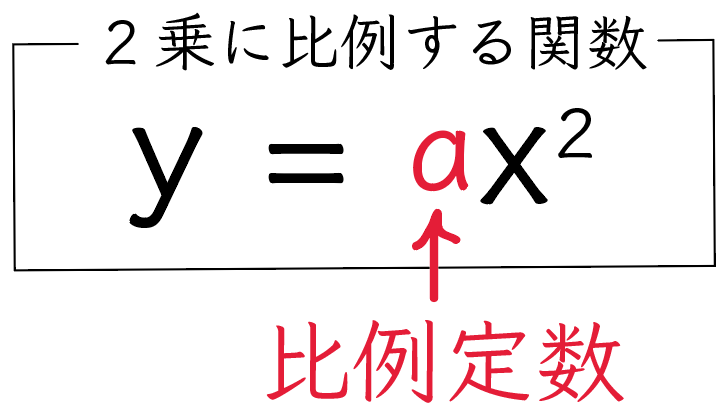
平方根の式を分配法則で計算する4つのステップ

平方根の式を分配法則で計算したい！

こんにちは！この記事をかいてるKenだよ。タコベルは欧米にかぎるね。

平方根の計算では、

• ルートの足し算・引き算
• ルートの掛け算
• ルートの割り算

をマスターしてきたね。

これでどんなルートの計算でもどんとこい・・・・・

・・・・

と思ったら大間違い。

まだまだ平方根・ルートの計算は奥が深い。

油断大敵ってやつよ。

今日は、ルート計算の応用として、

平方根の式を分配法則で計算する方法

を解説していくよ。

ここまでやっとけば大丈夫だ。

平方根の式を分配法則で計算する4ステップ

4ステップ踏むといいよ。

1. 分配法則をつかう
2. 根号をはずす
3. ルートを簡単にする
4. ルートの足し算・引き算する

例題をといてみようか。

Step1. 分配法則をつかう

分配法則で（）をはずそう。

分配法則って、

（）の前の数字を中の項に1つずつ掛けたものだったね。

⇒ 分配法則をわすれたときは復習してね^^

Qikeru：学びを楽しくわかりやすく

2014.11.11

【中学数学】分配法則のチョー便利な1つの使い方

https://media.qikeru.me/分配法則

 分配法則って何よ？？あんまり美味しそうじゃないけど。。こんにちは！この記事を書いているKenです。昼飯に焼き肉を食べました。 分配法則 (distributive property) という計算法則をご存知ですか？！　名前が超カッコイイこの法則は、中学1年生の数学でで登場します。はじめてこの数学用語をみかけた中学生の方は、は？？　分配？？？　お、おれの財産は渡せねえよう！とぶっきらぼうになってしまうかもしれません。そんな一見、超うさん臭い「分配法則」くんですが、じつは中学校の数学の中で、かなりかなりの重要度を誇...

例題でも分配法則が活躍だ。

（）をはずしてやると、

√2 (5 + √8) – √6 (√3 – 4)
= 5√2 + √16 -√18 + 4√6

になる。

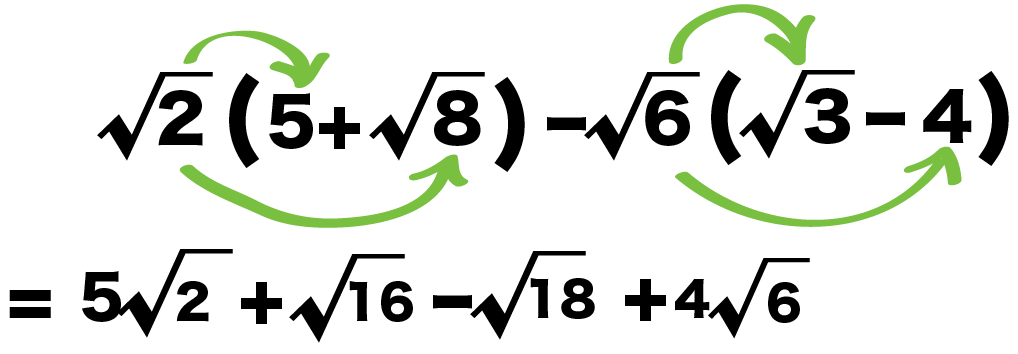
Step2. ルートを外す

ルートをはずそう。

中身が「なにかの2乗」なら外せるね。

練習問題では、

√16

のルートがはずれそう。

なぜなら、

中身が「4の2乗」になってるからね。

ルートをとると、

√2 (5 + √8) – √6 (√3 – 4)
= 5√2 + √16 -√18 + 4√6
= 5√2 + 4 -√18 + 4√6

になる！

Step3. ルートを簡単にする

ルートを簡単にしよう。

中身に「2乗の因数」があったら外にだせばいいんだ。

⇒くわしくはルートを簡単にする方法をよんでみて

Qikeru：学びを楽しくわかりやすく

2016.06.11

【平方根の計算】ルートを簡単にする方法がわかる3つのステップ

https://media.qikeru.me/square-root-simplification

平方根（ルート）を簡単にする方法ってなに？？こんにちは！この記事をかいてるKenだよ。朗読をはじめたね。 平方根の計算でよくつかうのは、ルートを簡単にする方法だ。ぶっちゃけ簡単にしなくてもいいんだけど、計算しやすくなるんだ。しかも、先生によってはルートが簡単じゃないと×にするから要注意。 そこで今日は、平方根（ルート）を簡単にする方法を解説していくよ。よかったら参考にしてみて。 = もくじ = ルートを簡単にするってなに？？ ルートを簡単にする方法  ルートを簡単にするとは・・・...

練習問題では、

√18

を簡単にできそうだ。

なぜなら、

「3の2乗」をふくんでるからね。

計算式の「√18」を簡単にすると、

√2 (5 + √8) – √6 (√3 – 4)
= 5√2 + √16 –√18 + 4√6
= 5√2 + 4 –3√2 + 4√6

になるね。

Step4. ルートの足し算・引き算する

最後は、ルートの足し算・引き算だ。

中身がおなじルート同士の整数を足し引きしよう。

⇒くわしくはルートの足し算・引き算をよんでみて

Qikeru：学びを楽しくわかりやすく

 

4 Pockets

2016.06.18

平方根（ルート）の足し算・引き算の仕方がわかる3つのステップ

https://media.qikeru.me/root-addition-subtraction

平方根（ルート）の足し算・引き算の仕方って？？こんにちは！この記事をかいているKenだよ。出会いは突然だね。 ここまで、 平方根の掛け算 平方根の割り算を勉強してきたね。こいつらはぶっちゃけ簡単。ルートの中身を掛け算・割り算すればいいからね。でもじつは、平方根の計算でめんどいのは、ルートの足し算・引き算なんだ。 足し算・引き算をマスターすれば大丈夫。どんな平方根の計算もクリアできるはずさ。今日はその、平方根（ルート）の足し算・引き算の計算方法を解説していくよ。よかったら参考にしてみてね。...

練習問題では、

• 5√2
• 3√2

の中身がいっしょだ。

整数部分を足し算・引き算してやると、

√2 (5 + √8) – √6 (√3 – 4)
= 5√2 + 4 -3√2 + 4√6
= 2√2 +4 + 4√6

になる。

おめでとう！

これで分配法則つかえちゃうね！

まとめ：平方根の式にだって分配法則はつかえる！

平方根の式にも分配法則はつかえる。

自分のペースでゆっくり（）をはずして、

計算問題をじわじわといていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。