【中学数学】分配法則のチョー便利な1つの使い方

分配法則って何よ？？あんまり美味しそうじゃないけど。。

こんにちは！この記事を書いているKenです。昼飯に焼き肉を食べました。

分配法則 (distributive property) という計算法則をご存知ですか？！　名前が超カッコイイこの法則は、中学1年生の数学でで登場します。

はじめてこの数学用語をみかけた中学生の方は、

は？？　分配？？？　お、おれの財産は渡せねえよう！

とぶっきらぼうになってしまうかもしれません。そんな一見、超うさん臭い「分配法則」くんですが、じつは中学校の数学の中で、かなりかなりの重要度を誇っています。

分配法則さえマスターすれば中学1年生の数学の大半を倒せます。中学1年生から数学の問題を倒せる武器を所持できるなんてうらやましいですね、まったく！

分配法則という武器を使いこなせ！！

今日はせっかくなので、

分配法則という最終兵器の概要を説明しながら、あまり知られていない便利な使い方まで紹介していきます。

分配法則の使い方がわからなくて悩んでいる方は参考にしてみてくださいね。

分配法則を一言で説明して！！ねえ？

分配法則をわかりやすく説明してくれたら欲しいものあ・げ・る

と美女に迫られたとしましょう。なんとしても欲しいものを手に入れたいぼくは、分配法則を次のように説明するかもしれません。それは、

分配法則とは、たし算とかけ算の橋渡しの法則のことだね^^

と。たぶん、こんなきざな台詞を使えば、美女も・・・・・

なんて妄想はさておき。なぜ分配法則が「たし算とかけ算の橋渡しの法則」になるのか確認していきましょう！

分配法則のあらまし

分配法則は中学数学の教科書で以下のように説明されています。

a, b, cという3つの数字による計算式があったとしましょう。分配法則を使うとこの文字式は次のように書き換えることができます。

$$a\times(b+c)=a\times b+a\times c$$

です。えっ。文字ばっかりで分かりづらいですって？！？　そんな方のために実際の数字で分配法則を考えてみましょう。上のa, b, cを４、５、６という数字で置き換えてみると、

となります。

左の計算式を右のようにべつの形で書き換えられるわけです。このように左辺から右辺に式を変更することを分配法則を使っちゃる、といい、ちまたでは「カッコをはずす」なんて異名で呼ばれています。

まとめると、

計算式の()をなくせる法則を「分配法則」と呼んでいるわけです。

分配法則ってホントに便利なの？？？？

分配法則が便利なケースっていったいどんな場合でしょう？？

さっきの説明では全然分配法則が役に立つ気配ありませんよね？？？　むしろ足を引っ張っているような気がします。

たとえば、先ほどの例であるでは余計に左辺の式を複雑にしています。なんだろう、このままでは分配法則なんて消え失せろなんて言われそうです。

そこで、読者の方が分配法則に惚れ直すことを願い、分配法則がむちゃくちゃ効力を発揮しているケースを紹介していきます。

「桁数の多い数字」×「一ケタの数字」

分配法則が役に立つケースの1つとして挙げられるのは、

「桁数の大きい数字」×「1ケタの小さい数字」という計算

です。たとえば、

のような計算式。この2ケタ×1ケタ数字のかけ算は、そろばんを習っていないと瞬殺できません。ぼくはそろばんを習っていないので、この計算を終了させるのに5分ぐらいかかりそうです。えっとお、小学校で勉強した筆算の方法を利用して、

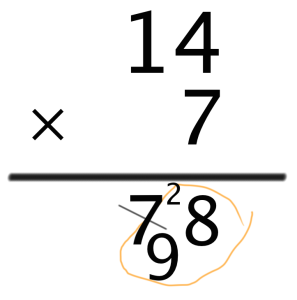
なんて感じです。じつは小学校で勉強した通りに筆算の公式を利用せずとも、この計算を瞬殺する方法があるんです。それは、

分配法則をつかって桁数の大きい数字をばらしてあげる

という方法です。えっ？　どういうことなのか意味不明ですって！？？

それでは詳しくわかりやすく説明していきましょう。

ステップ1. 桁数の大きい数字をたし算の形に直す

まずは桁数の大きい数に注目します。という計算式でいえば、がそれに値します。

このときのポイントは、

きりのいい桁数でわけわけする

ことです。つまり、14の場合ですと、10がきりのよい桁数です。14を「10と4が足された数字」と捉え直してやるわけですね。

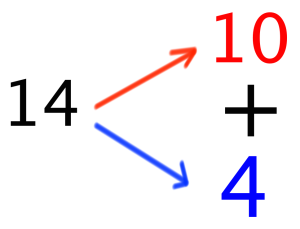
すると、という計算式は、

という()を含む計算式に変化させることができます。

ステップ2. 分配法則を用いて()をはずす

桁数の大きい数字をたし算の計算式に変換したら、分配法則の出番です。記事の初めで学んだ「分配法則」をつかって式中の()をはずしてやると、

となります。え？余計に計算過程が増えてしまったですって！？？　た、たしかにその感は否めません。だがしかし、の前の項のという計算はえらくカンタンです。なぜなら、10を7にかけるだけですからね。すると、

と答えを導くことができます。14を(10+4)に変形して分配法則で()をはずす。これだけで難しい桁数の大きいかけ算もとけることになります。

この分配法則の活かし方は桁数が増えても同じです。たとえば、といった具合にです。この3ケタと1ケタのかけ算にも分配法則を適用してやると、

なぜ分配法則は「橋渡し法則」と呼ばれるの？？

それじゃあ、なぜぼくは分配法則を「橋渡し法則」と呼んでしまったのでしょうか！？　さっきまでの説明に橋なんて1個も登場しませんでしたね。これじゃあ、嘘をついた罪で逮捕されそうです。

先ほどの計算式をよーーく見つめてみてください。

これです。これ。

この数式を長いこと見つめていると、

分配法則により、かけ算が足し算になったり、足し算がかけ算になったりしている、

ということが分かります。

14という数字を(10+4)というたし算の形にしたり、をという足し算とかけ算が混じる計算式に変換したりと大忙しです。ま、まさに、分配法則は「たし算とかけ算の橋渡し法則」ですね！

それでは、また今度です！

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。