平方根（ルート）の割り算の計算方法の5つのステップ

平方根（ルート）の割り算の計算方法がわからん！？

こんにちは！この記事をかいてるKenだよ。湿度はほどほどね。

ルートの計算にはいろいろある。

足し算、引き算、掛け算・・・って感じでさ。

もうね、ありすぎて疲れちまうよ。

今日はルート計算をマスターするために、

ルート（平方根）の割り算の仕方

を勉強していこう。
 

= もくじ =

1. ルート割り算の基本ルール
2. 割り算の計算方法

ルート（平方根）割り算の基本ルール！

ルートの割り算には基本ルールがある。

それは、

分子・分母のルートをいっしょにしてもいい

ってやつだ。

たとえば、√a、√bがあったとすると、

√b 分の √a = √(b分のa)

になる。

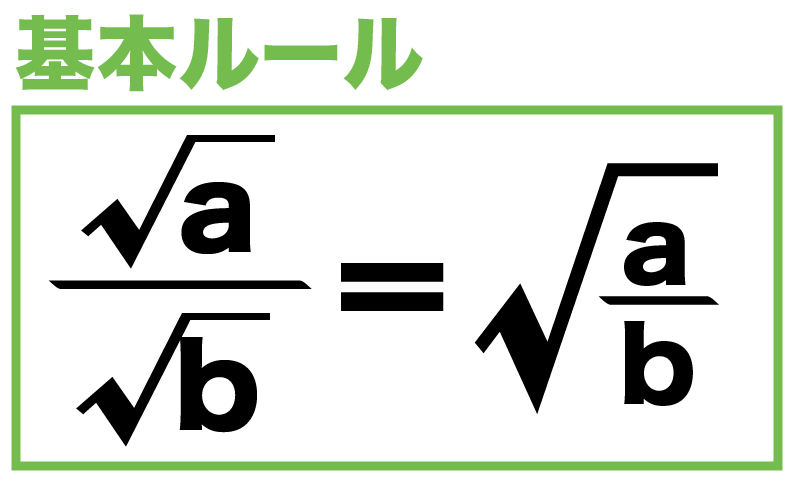
えっ。これが割り算と関係があるのかッテ？？！

そうだね。

割り算は分数であらわせたよね。

a÷b

なら

b分のa

って感じで。

÷のうしろの数を分母に、それ以外を分子にもってきてるわけ。

これをルートの割り算でもつかうと、

√a÷√b = √b分の√a

になるんだ。

んで、これにさっきのルールでつかうと、

√a÷√b = √b分の√a = √(b分のa)

になる。

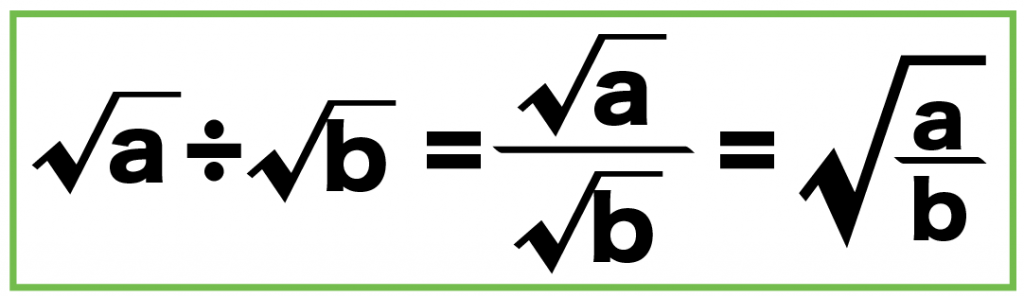
そして、途中の真ん中をはぶくと、

√a÷√b =√(b分のa)

になるね。

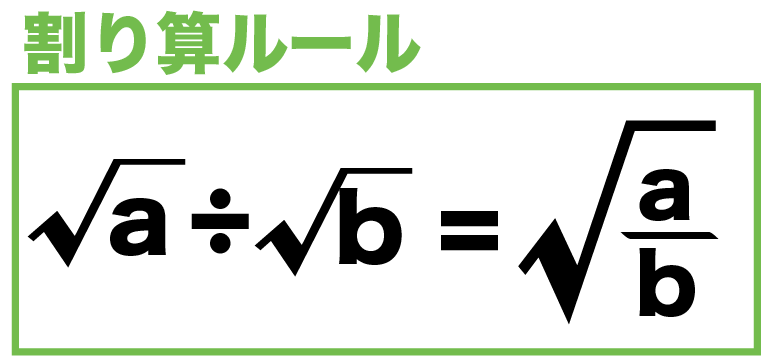
つまり、

√をいっしょにして、÷の後ろを分母にしてもいいんだ。

これがルート割り算の基本ルールだ。

平方根（ルート）の割り算の5つのステップ

ルートの割り算は5ステップでいけるよ。

1. ルートを簡単にする
2. 割り算を分数にする
3. ルートを一緒にする
4. 約分する
5. 分母を有理化する

例題をいっしょにといてみよう。

例題

つぎのルートの割り算を計算してください。

√24 ÷ √10

Step1. ルートを簡単にする

ルートを簡単にしよう。

ルートの中身から2乗の因数を外にだせばいいんだ。

⇒ ルートを簡単にする方法はコチラ

例題では、

ルート24

が簡単にできそうだね？？

なぜなら、素因数分解すると、

24 = 2の3乗 × 3

になるからね。

ルートの外に「2の2乗」をとりだせそうだ。

√24を簡単にすると、

√24  ÷√10
= 2√6 ÷ √10

になるね！

Step2. 割り算を分数にする

割り算を分数にしよう。

やり方は簡単。

「÷の後ろの数」を分母にもってくればいいのさ。

√a÷√bなら、

√b分の√a

ってかんじにできる。

例題の割り算では、

√10

が÷の後ろにきてるね？？

だから、こいつを分母にもってくると、

√24  ÷ √10
= 2√6 ÷ √10
=√10分の2√6

になるよ。

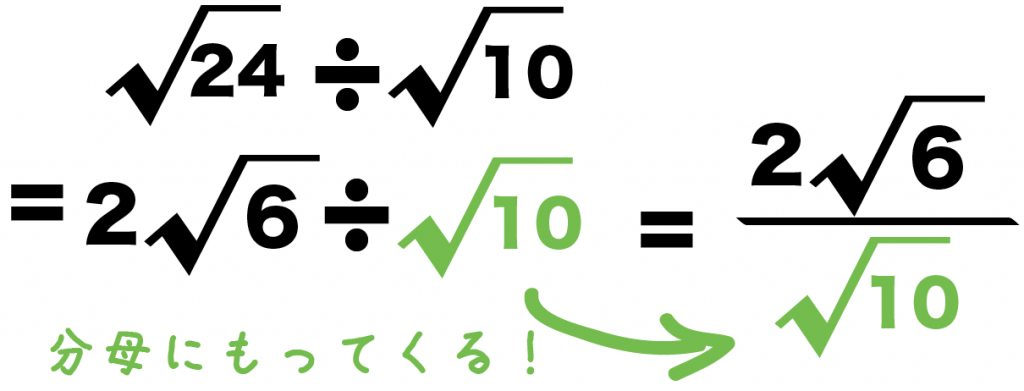
Step3. ルートを1つにする

分数を1つにまとめよう。

√b 分の √a = √(b分のa)

っていう基本ルールをつかえばいいのさ。

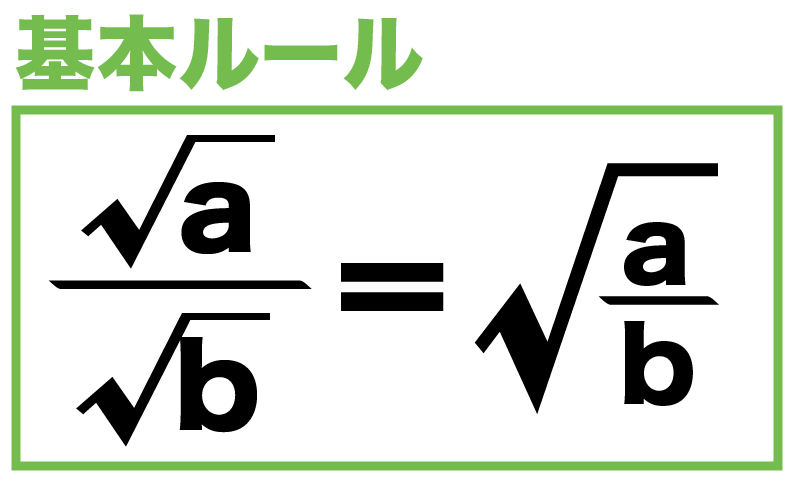
例題でもおなじ。

√10分の√6

のルートをいっしょにしてあげると、

√24  ÷ √10
=√10分の2√6
= 2×√(10分の6)

になるね！

Step4. 約分する

ルートの中身を約分しよう！

スッキリしていいじゃん！？

例題のルート内の分数は、

10分の6

だね？？

こいつを約分すると、

5分の3

になる。

だから、さっきの計算式は、

√24  ÷ √10
= 2×√(10分の6)
= 2×√(5分の3)

になるんだ。

Step5. 分母を有理化する

最後に、分母を有理化しよう。

分母の平方根を分子と分母にかければいいのさ。

⇒くわしくは「分母の有理化のやり方」を読んでみてね^^

例題の分母は√5。

だから、分子と分母に√5をかけると、

√24  ÷ √10
= 2×√(5分の3)
= 5分の2√15

になるね。

おめでとう！

これでルートの割り算マスターだ^^

まとめ：ルートの割り算の計算方法は長い

平方根の割り算の仕方はどう？？

5ステップあるからなげえかもしれない。

だけど、どのステップも基本的なこと。

ルートの割り算に必要なものをしっかり
 

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。