一次関数の変域の求め方を知りたい!
こんにちは!この記事をかいているKenだよ。換気は大事だね。
一次関数の変域の問題ってよくでるよね。
たとえば、つぎのような問題さ。
例題
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
一次関数の変域とかあきらかにむずそうだけど、
基本をおさえればチョー簡単なんだ。
今日はこのタイプの問題を攻略するためにも、
一次関数の変域の求め方がわかる3ステップ
を紹介するよ。
よかったら参考にしてみて。
一次関数の変域の求め方がわかる3つのステップ
3ステップで変域を求められるよ。
- 変域の端と端を代入する
- 小さい方を左、大きい方を右にかく
- 不等号は同じやつを使う
例題をいっしょにといてみよう!
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
Step1. 変域の端と端を代入する
まず、変域の端と端を代入してやろう。
たとえば、xの変域が○ ≦ x ≦ □だとしたら、
- x = ○
- x = □
を一次関数に代入すればいいんだ。
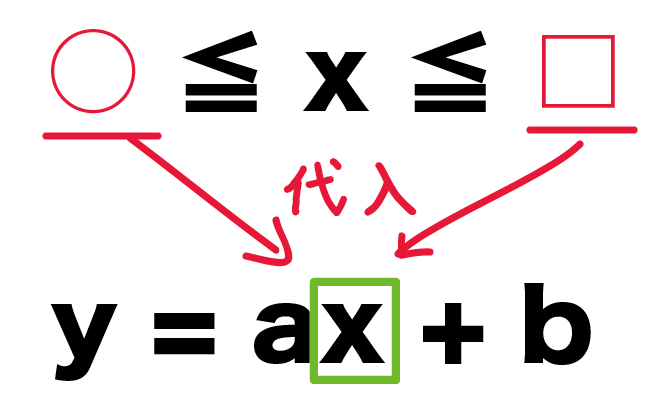
例題でわかっているのはxの変域の、
-1 ≦ x ≦ 9
だね。
この変域の端っこの、
- x = -1
- x = 9
を一次関数 y = -3x + 7 に代入すればいいんだ。
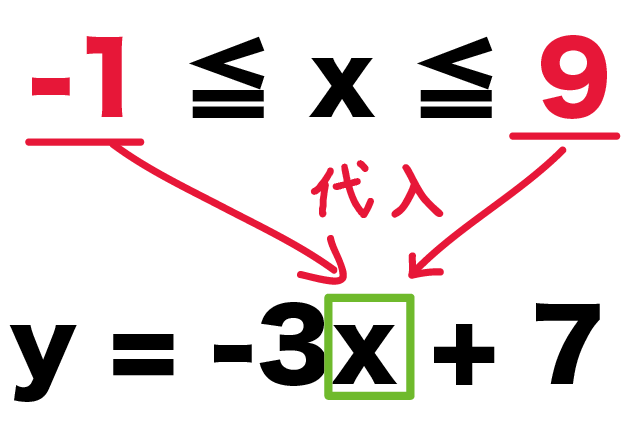
x = -1 を代入すると、
y = -3x + 7
= -3 × (-1) + 7
= 10
になる。
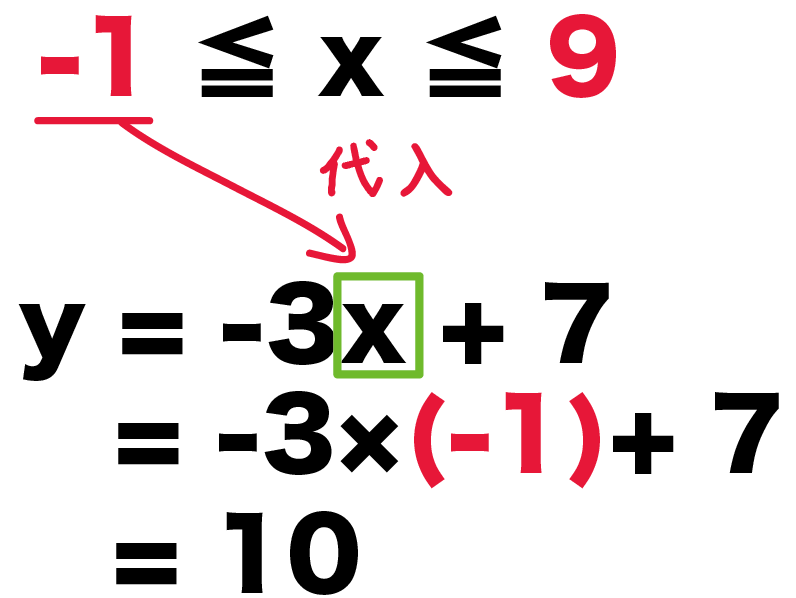
一方、x = 9を代入してやると、
y = -3x + 7
=-3 × 9 + 7
= – 20
になるね。
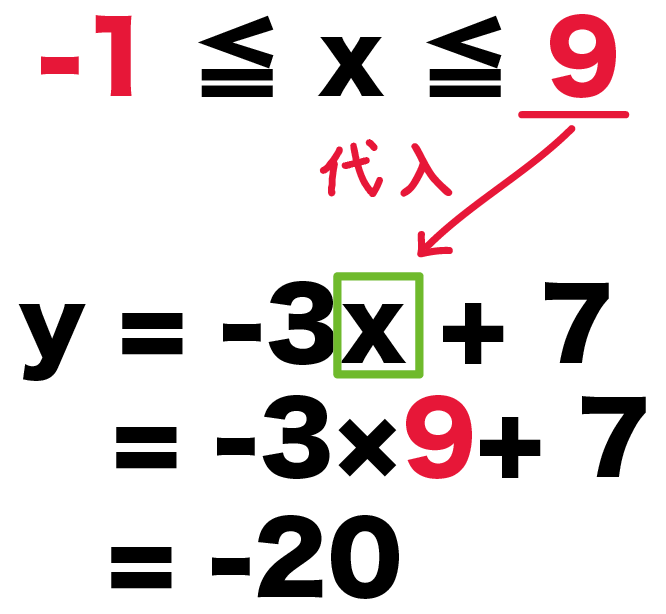
これが第1ステップ!
Step2. 小さい値を左、大きい値を右にかく
さっき計算した2つの値のどちらが大きいのか??
を比べてみよう。
そして、
大きい値を右に、小さい値を左にかくんだ。

例題では、
- y = 10
- y = -20
の2つをゲットできたね??
こいつらを比べてみると、
明らかに10のほうがでかい。
-20のほうが小さいね。
だから、10を右に、-20を左にかいてみて。

これが第2ステップ!
Step3. 不等号でむすぶ!
最後は不等号で結んでみよう。
使う不等号は、
問題でわかってる変域と同じものを使うよ。
例題でいうと、xの変域は「≦」を使ってるよね??
だからyの変域も「≦」を採用するのさ。
例題をみてみよう。
「大きい値」と「小さい値」の間に「y」をかく。

そして、
「小さい値」・「大きい値」と「y」を「≦」で結んでやるのさ。
-20≦y≦10

これでyの変域が求まったよ。
おめでとう^^
なぜ一次関数の変域が求められるんだろう??
でもさ、なんで変域が求められるんだろう??
話がうますぎるよね。
じつは、ここだけの話なんだけど、
一次関数がまっすぐだからなんだ。
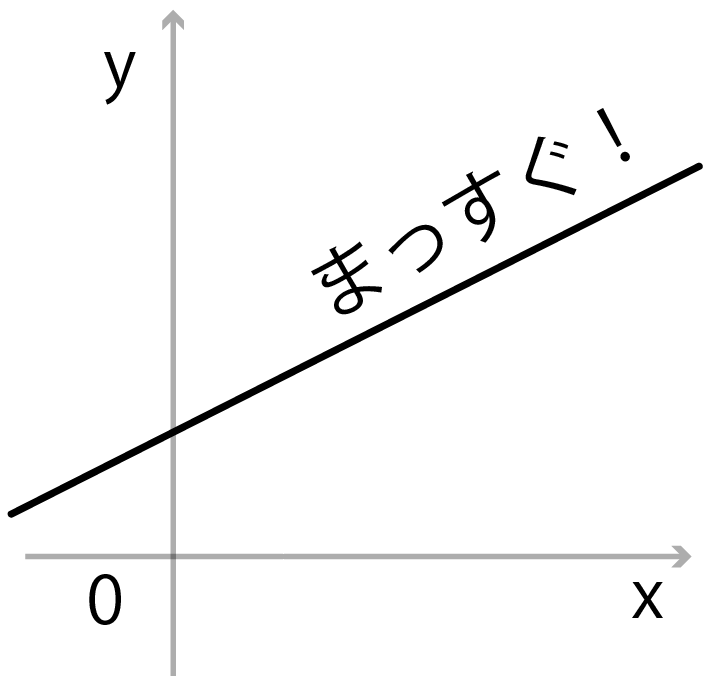
xの変域の端っこと端っこのy座標が、
yの変域の端っこと端っこになっているよ。
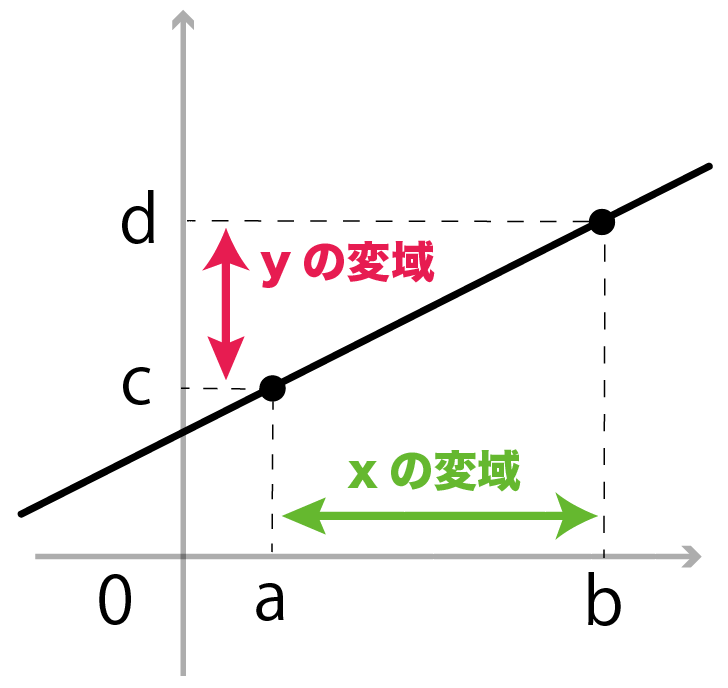
これは傾きがマイナスでも同じだね。
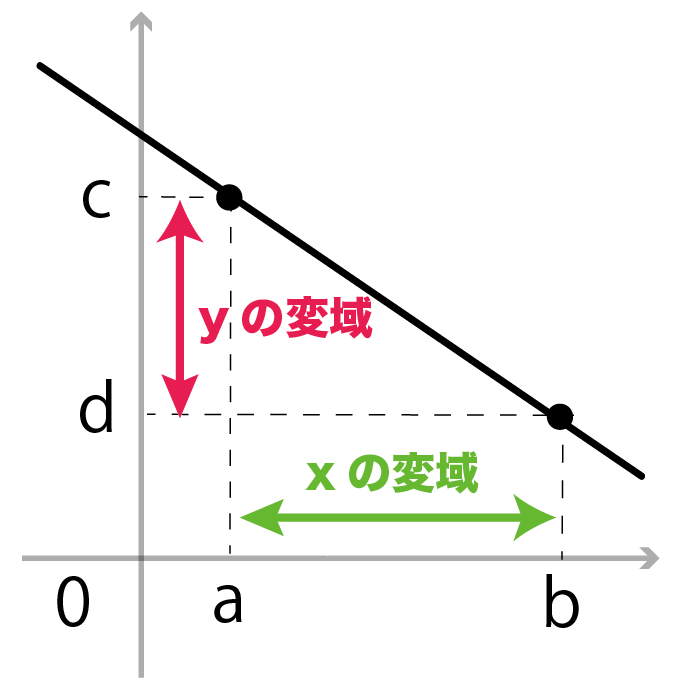
もし、一次関数が波だっていたり、
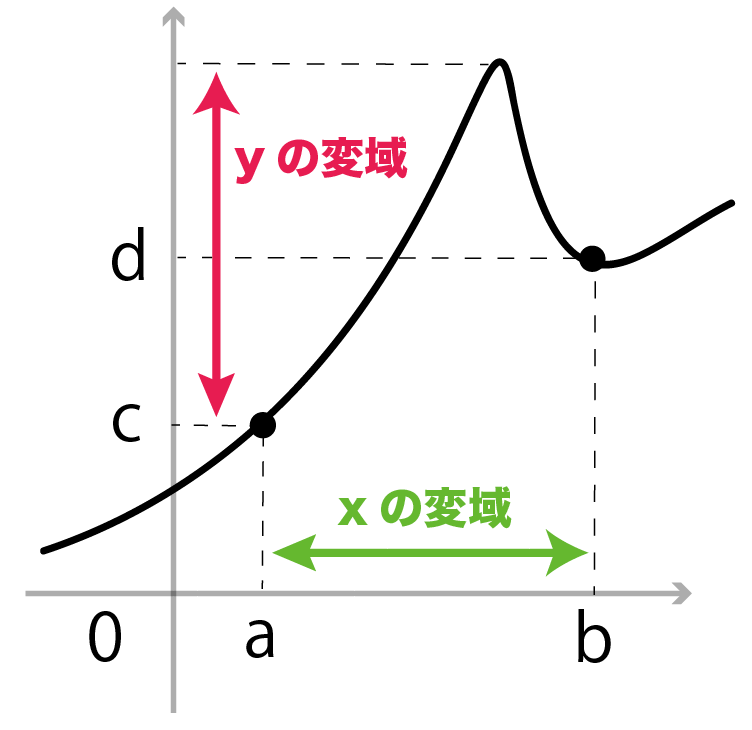
ギザギザしていたら変域はこのやり方だと無理。
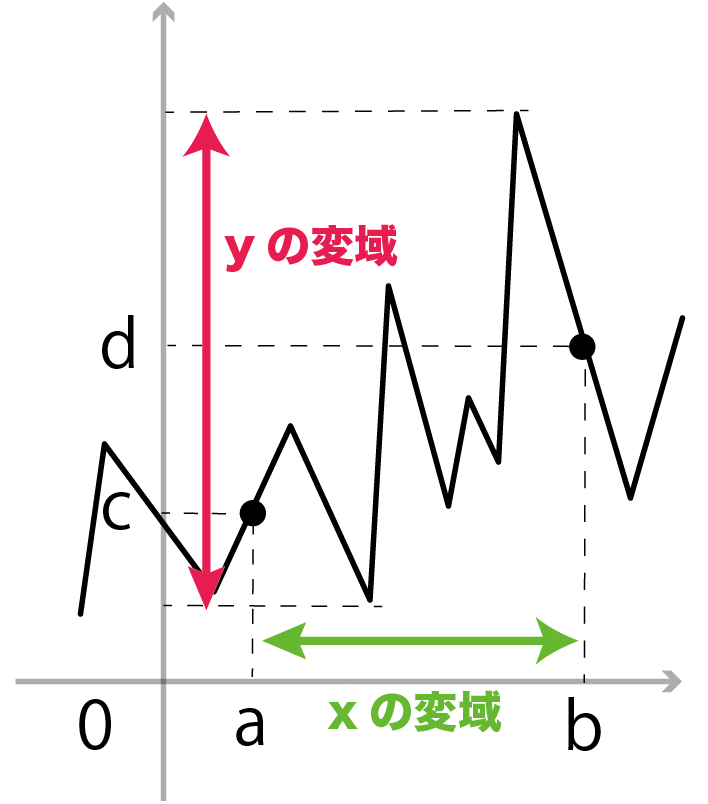
なぜなら、変域の端っこ以外に、
最大値とか最小値がいるかもしれないからね。
一次関数がまっすぐだからこそ、変域の端っこが最大値・最小値になる
ってことを覚えておこう!
まとめ:一次関数の変域の求めるためには端をつかえ!
一次関数の変域の求め方は簡単。
- 変域の端っこを2つ代入
- 小さい順に並べ替える
- 不等号で結ぶ
の3ステップでいいんだ。
問題をといて変域に慣れていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。

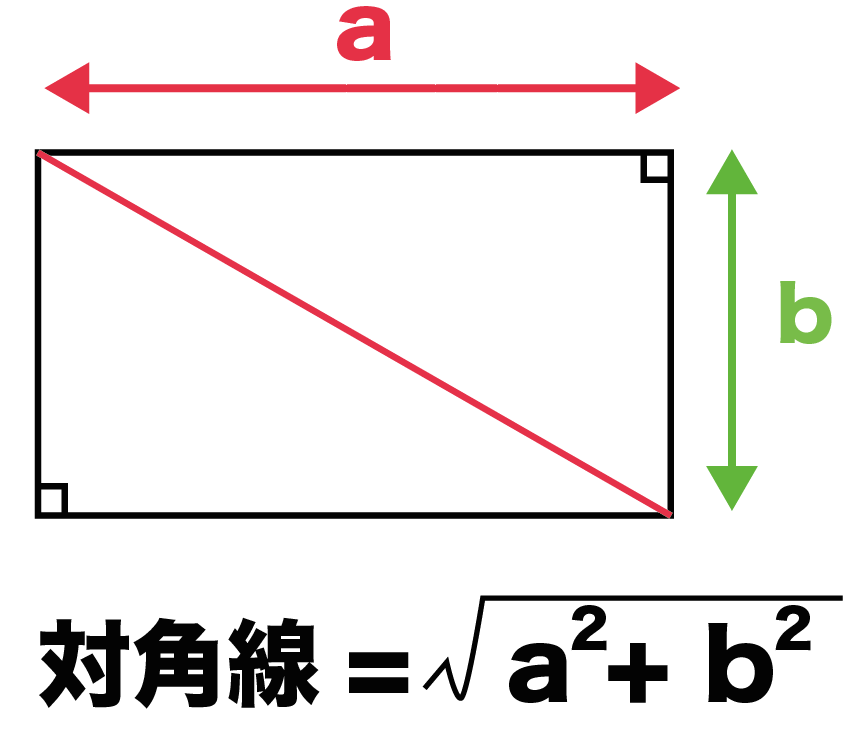




正方形ABCDを示したものでAB=10センチ点Pは、頂点Bから出発してからの問題
3秒後の値を求めよ
>正方形ABCDを示したものでAB=10センチ点Pは、頂点Bから出発してからの問題
3秒後の値を求めよ
Bの速さとかによるかな
関数y=ax+6(aは定数)は、xの変域が-2以上未満x以上未満2のとき、yの変域が0以上未満y以上未満bである。a以上0のとき、a、bの値を求めなさい。
y=ax+1(a>0)は変域が4≦x≦Bのとき
yの変域が9≦y≦bです。
aとbは?
>関数y=ax+6(aは定数)は、xの変域が-2以上未満x以上未満2のとき、yの変域が0以上未満y以上未満bである。a以上0のとき、a、bの値を求めなさい。
aが0以上ってことは、xが大きくなるほどyはどうなる?小さくなる?それとも大きくなる?
とても分かりやすかったです!^^
>y=ax+1(a>0)は変域が4≦x≦Bのとき
yの変域が9≦y≦bです。
一次関数で傾きが+のとき、xが大きくなればなるほどyはどうなる?
これがわかればxが最小値4を取った時、yが最大値、最小値のどっちを取るかわかるね
ありがとう!励みになるぜ!
≦の=の謎が解けません! いつも丁寧で分かりやすいです(*^-^*)
>≦の=の謎が解けません!
不等号の意味をよんでみて!
y=4分の1x+2 xの変域がx=>-8のときの、yの値を求めなさい。これが分かりません。教えてください
>y=4分の1x+2 xの変域がx=>-8のときの、yの値を求めなさい。これが分かりません。教えてください
変域の問題は図を書くとわかりやすいよ。
xが-8より大きいってことは、傾きが正の関数の場合、
yはxが-8のときの値よりも大きいってこと
変化の割合が分数のときはどうやるのでしょうか。。
例えば、
y=-3分の2x+6の式で、yの変域が-2≦y≦10となるようなxの変域は
どのようにして求めれば良いのでしょうか?
>y=-3分の2x+6の式で、yの変域が-2≦y≦10となるようなxの変域
傾きが分数でもやり方は一緒だよ。
まずは図にかいてみよう。
例えば
y=3x−1 (−2≦x≦5) などの大なりイコール小なりイコールの計算は分かりましたが、例えば
y=−3分の4+2 (x<−6)などの大なり,小なりの計算はどうなりますか?
>y=−3分の4+2 (x<�−6)などの大なり,小なりの計算はどうなりますか? 大なりでも小なりでも同じだよ。 変域が最小値か最大値のどちらかを表してるはずだからね!
Y=-2/3×+6yの変域が-2 ≦y ≦10。
X の変域を求めろ。はどうすればいいのかわかりません。
>Y=-2/3×+6yの変域が-2 ≦y ≦10。
この問題のポイントは傾きがマイナスってこと。
マイナスってことは、yが最大値をとる時はxが最小値のはずだ!その逆またもしかり!
とても丁寧で分かりやすかったです。
すごく悩んでいた問題があっという間に解けてしまいました。ありがとうございました。
すみませんが、ここでひとつ質問をさせて頂きます。
yの変域の求め方はよく理解したのですが、xの変域を求めるにはどうしたらよいのですか?
xの変域も代入で求められますか?
>すみませんが、ここでひとつ質問をさせて頂きます。
yの変域の求め方はよく理解したのですが、xの変域を求めるにはどうしたらよいのですか?
xの変域でも求め方は一緒だよ!
傾きが+なら、yが最大値の時、xも最大値。
傾きがーなら、yが最小値の時、xも最小値だ。
式を自分で求めてその次に変域を求める問題があるんですけど、その式が求められません!
>式を自分で求めてその次に変域を求める問題があるんですけど、その式が求められません!
問題によるよね!
基本は連立方程式を解いて式を求めるよ
とても分かりやすかったです。
ありがとう!!
やっぱり「yの変域を求めなさい」に弱いです。できればもう少し簡単に教えていただければ幸いです。よろしくお願いします。
>やっぱり「yの変域を求めなさい」に弱いです。できればもう少し簡単に教えていただければ幸いです。よろしくお願いします。
一次関数の変域のポイントは、
傾きがプラスかマイナスか?
ってことだね。プラスだったら、xが最大値をとる時、yも最大値。マイナスだったらxが最小値ならyが最大値。
グラフをかいてみるとわかりやすいよ
ダイヤグラムの問題がわからないので教えてほしいです
>ダイヤグラムの問題がわからないので教えてほしいです
問題送ってみて!
学校の授業よりもわかりやすいです。
ありがとう!!
解決できました!
ありがとうございます!
めちゃくちゃわかりやすかったです !!!!
なんか軽い感じすきです ( 語彙力 )
ありがとう笑!
ほんまにありがたいで。マジで大好きよ。
分かりやすかったです。。今まで全く分からなかったのがこんなすぐに理解できるとわ思わなかったですww
ありがとう!!
わかりやすすぎてびっくりしましたありがとうございます
すごくわかりやすかったです。
「エックスの変域で≧を使っているから、yも≧を使う」とあるんですけど、自分が使っている教材の答えは、一次関数がy=−3x-2で、xの変域が−3≦x<2の時の答えが-8x≦y<7ではなく、-8<y≦7なんですけど、これはどういった原理なんでしょうか…
めっちゃめっちゃ分かりやすいです!
助かりました。
ありがとうございます!!!
めちゃくちゃ分かりやすかったです!ありがとうございます!!
Y=8x-4(2<x<5)の場合は?
すごく分かりやすいです!
ありがたい。。。。
「拓海さんは、家から3310m離れた図書館に向かって、途中の公園までは分速120mで走り、公園から図
書館までは分速70mで歩いたところ、合計33分かかりました。拓海さんが公園から図書館まで歩いた
時間をx分とした時の、公園から図書館までの道のりを、求めなさい」
↑の問題が分かりません。
どうか教えて下さい。
とても分かりやすかったです。(^^)d
なるほど、、