正三角形の角度の求め方がわからん??
こんにちは!この記事をかいてるKenだよ。白米、最高。
正三角形の角度ってシンプル。
内角の1つの大きさは、
60°
なんだ。
しかも、ぜーーーんぶの内角が60°になっているよ。
先生に、
正三角形の角度はいくつ??
ってきかれたら、
60°ですがなにか??
っていえばいいよ。

今日はもう一歩ふみこんで、
正三角形の角度の求め方
を勉強してみよう。
なんで角度が60°になるんだろう・・・・
っておもったら読んでみてー
正三角形の角度の求め方がわかる3ステップ
なぜ、正三角形の角度が60°になるのか??
をみていくよ。
例として、つぎの正三角形ABCをとりあげる。
3ステップで角度を求められるよー
Step1. 「角度を文字でおく」
1つの角度を文字でおこう。
正三角形ABCでは、
角B = a
としてみたよ。
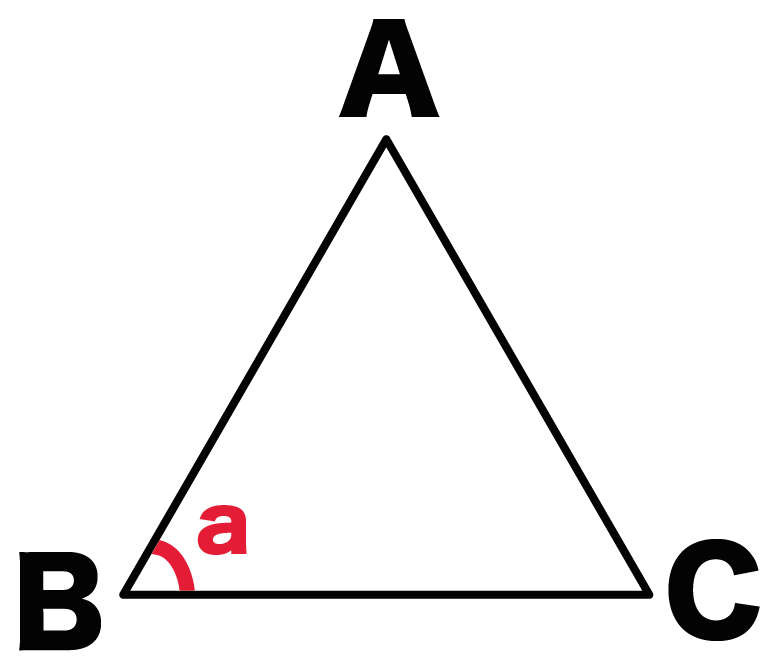
文字はなんでもいいよ。
bでもcでもxでもね。
Step2. 「底角が等しいことをつかう!」
つぎは二等辺三角形の性質である、
底角が等しい
という性質を使うよ。
正三角形の定義は、
3つの辺がすべて等しい三角形
だったよね?
ってことは、
2つの辺が等しい「二等辺三角形」でもあるわけだ。
例の正三角形ABCでいうと、
AB = ACの二等辺三角形ってことだね。
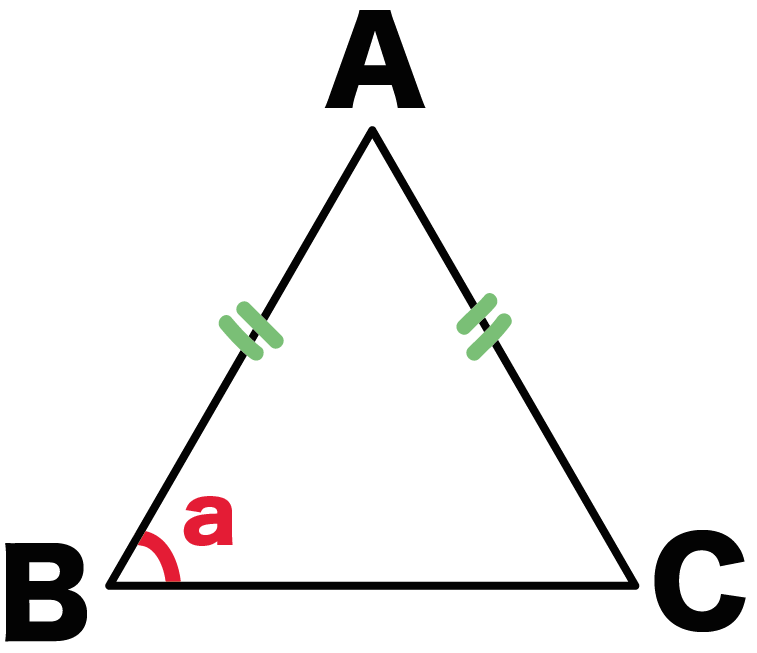
底角は等しい
という二等辺三角形の性質をつかってやれば、
角B = 角C = a・・・・(1)
であることがわかる。
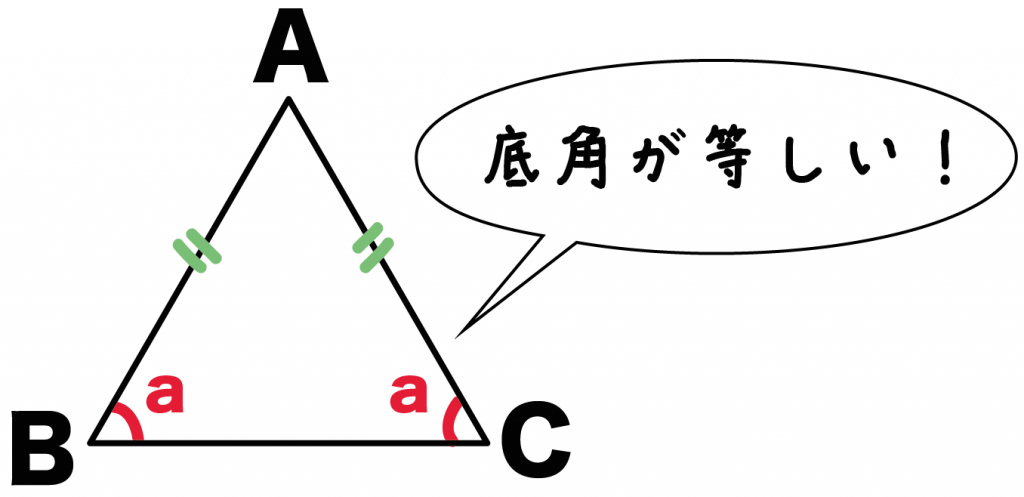
おなじように、
正三角形ABCは、
AC = BCの二等辺三角形でもあるわけだ。
だから、ここでも底角が等しいことを使ってやれば、
角A = 角B = a ・・・・(2)
ってことがいえるね。
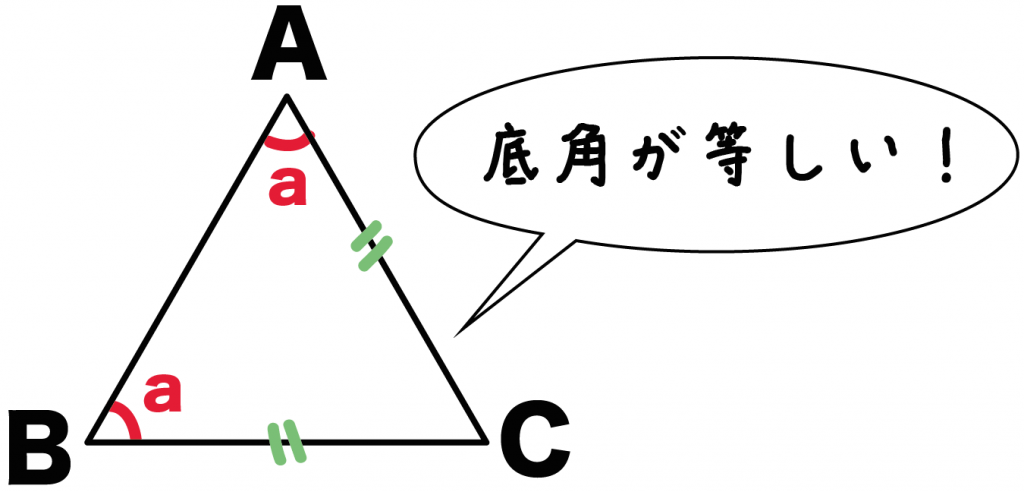
(1)、(2)より、
角A = 角B = 角C = a
ってことがいえるんだ。
だから、
ぜーーんぶ角度が同じってことになるのさ。

Step3. 「内角の和を3でわる!」
正三角形の角度はぜーんぶ等しい。
ってことは、
1つの角度は、
内角の和を3でわったもの
ってことだ。
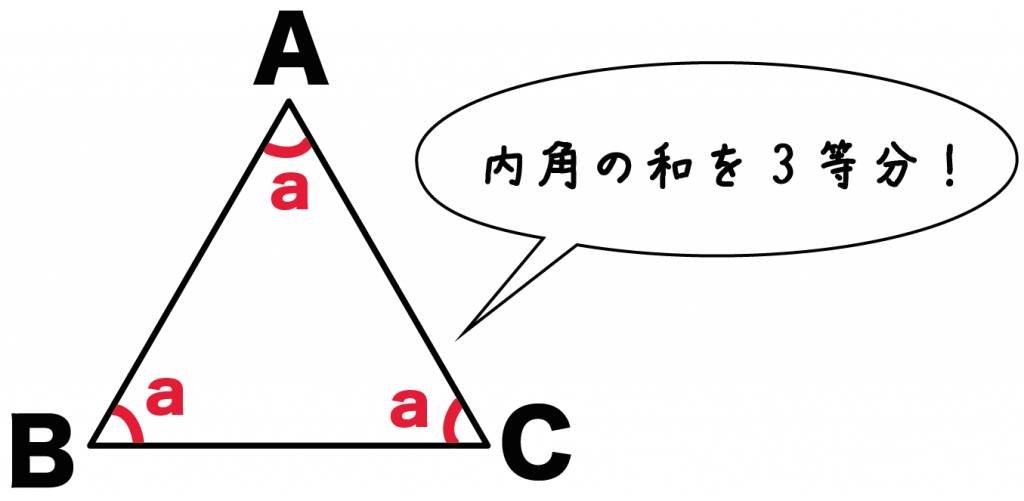
三角形の内角の和は180°なので、
180を3でわってやると、
180÷3
= 60°
になるね!
よって、正三角形の1つの角度は「60°」になるんだ。

まとめ:正三角形の角度の求め方は底角をつかえ!
角度の求め方で大事なのは、
正三角形を二等辺三角形としてあつかえるか?
だ。
底角が等しいことをつかって、
問題をといていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





一辺の長さが10センチの正三角形の高さがわかりませんどうやるば求まりますか?
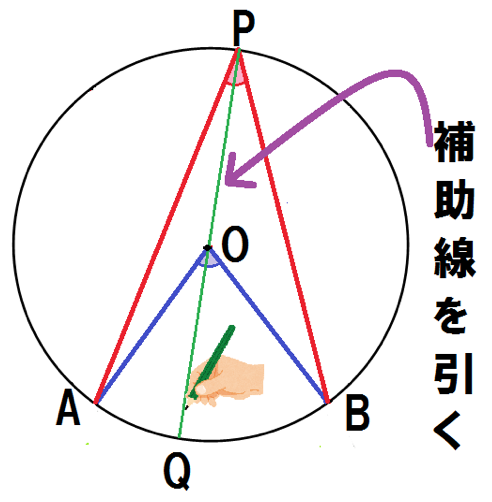
頂点から垂直二等分線を底辺に下ろしてみて。
直角三角形が2つできるから、そこで三平方の定理を使えばオッケーだ。
詳しくは「【簡単公式】正三角形の高さの求め方がわかる3ステップ」を読んでみて!
相似の三角形の探し方
相似条件はいろいろあるけど、だいたい2角が等しいってやつだから
2つの角度が等しい三角形を見つけて行こうぜ
正三角形ABCの辺BC,AC上にBC=CEとなるように,それぞれ点D,Eをとり,BEとADの交点をFとする。この角FDB+角FBDの大きさを求める。という問題が分かりません。どのように求めたらいいですか?
三角形ABCの∠B ∠Cの二等分線の交点をDとする。∠BDC=3∠BACのとき、∠Dの大きさを求めなさい。