【簡単公式】二等辺三角形の面積の求め方がわかる3ステップ

二等辺三角形の面積の求め方の公式って？？

こんにちは！この記事をかいているKenだよ。卵は便利だね。

二等辺三角形の面積の求め方には公式があるよ。

底辺をa 、高さをhとすると、

1/2 ah

つまり、

底辺×高さ÷2

で計算できちゃうんだ。

たとえば、

• 底辺 = 4 cm
• 高さ= 8 cm

って二等辺三角形があったとしよう。

公式で面積を計算すると、

底辺×高さ÷2
= 4×8÷2
= 16 [cm²]

になるんだ。

どう？むちゃちゃ簡単でしょ？？

二等辺三角形の面積の求め方の公式がつうじない！？

だがしかし、しかし。

公式だけじゃ解けないときも、ある。

たとえばつぎの問題だ。

この問題では、

底辺と高さがわからない！！！

っていうパニックにおちいると思う。

公式に頼ってたら焦るねw

この問題を攻略するポイントは、

「等しい辺」を底辺にかえる！

ことさ。

これなら3ステップで攻略できちゃうんだ。

Step1. 補助線をひく！

まず、補助線をひこう。

「底角」から「等しい辺」に「垂線」をひっぱるだけでいい。

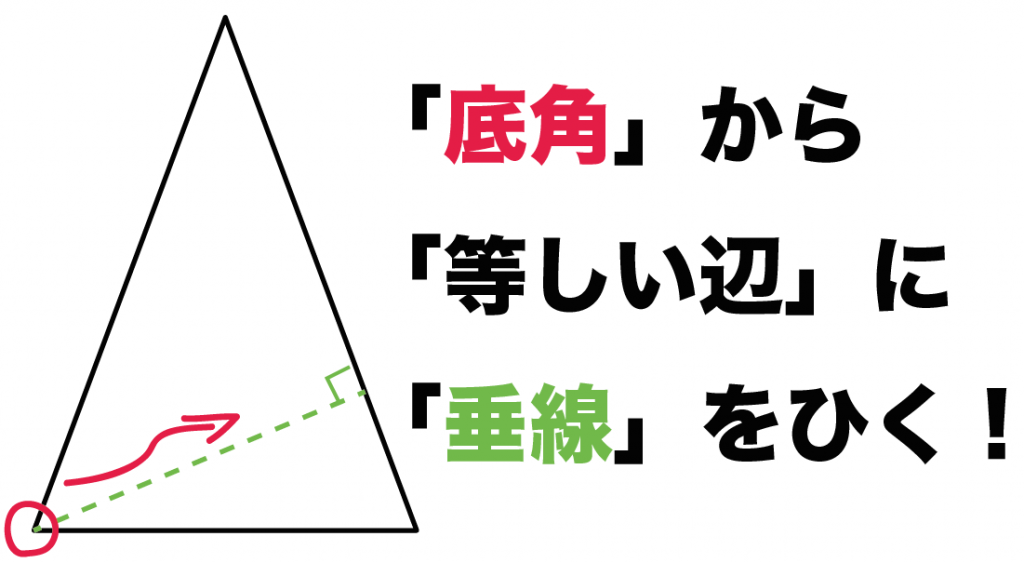
この「垂線」が二等辺三角形の「高さ」になるよ。

例題をみてみよう。

「底角C」から、

「辺AB」に垂線をひいてみる。

ABの延長と垂線の交点をHとしてみよう！

これで高さ「CH」をゲットできたね。

Step2. 二等辺三角形の「高さ」を計算！

さっきの「高さ」を計算してみよう。

こいつは何cmになんだろう？？

例題でいうと、

角CAHの大きさは三角形の外角の定理より、

角CAH = 角ACB + 角CBA
= 15 + 15
=  30°

になるね。

ここで、

三角形CAHに注目してみよう。

こいつは角H = 90°の直角三角形で、

斜辺AC = 10cm

だね？

んで、

角CAH = 30°だから、

CH はACの1/2になっているはずだ。

よって、

CH = 5 cm

になるね。

Step3. 公式で面積を計算！

公式で面積を計算しよう！

底辺×高さ÷2

っていう公式をつかうためには「底辺」と「高さ」が必要。

「高さ」をStep2で求めたので、

あとは、

「底辺」だけだね。

底辺は垂線をひっぱった先の辺になるよ。

例題でいうと「辺AB」が底辺になるね。

んで、

高さは「垂線CH」さ。

公式で面積を計算すると、

10×5÷2
= 25[cm²]

っていう答えがでるね。

おめでとう！

これで二等辺三角形の面積を計算できたね！

まとめ：二等辺三角形の面積の求め方は補助線で一発！

二等辺三角形の面積を求める問題で、

高さがないんだけど！？？？？

って焦ったとき。

こういときは、

等しい辺に補助線の垂線をひいてあげよう。

問題をときまくって慣れていこうね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。