【簡単公式】多角形の対角線の本数が5秒でわかる求め方

対角線の本数の求め方に公式ってあるの？？

こんにちは！この記事をかいているKenだよ。本屋がよんでるね。

多角形の対角線の本数の求め方には公式があるよ。

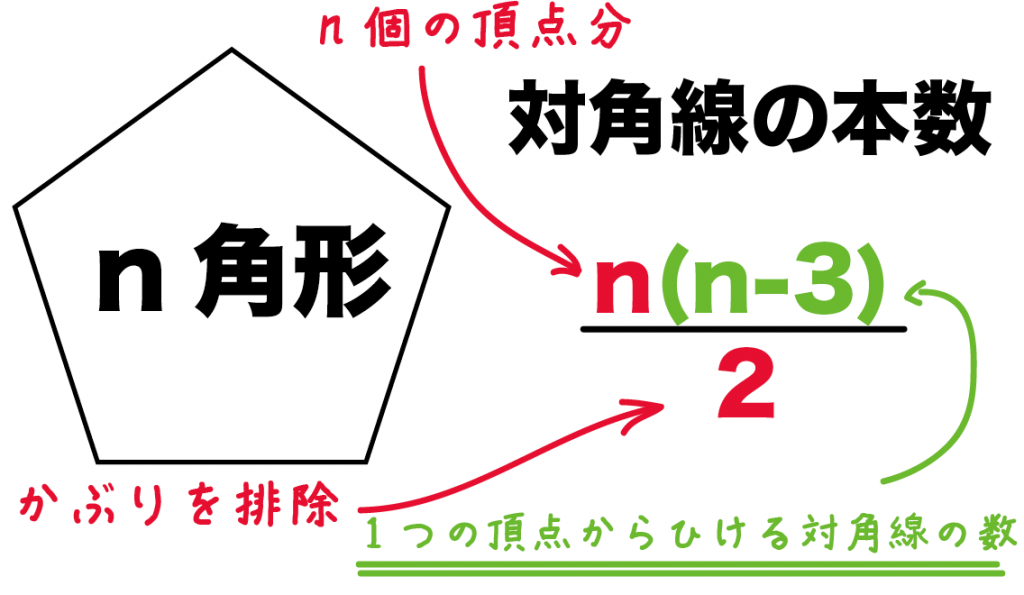
n角形の対角線の本数は、

n(n-3)÷2

で計算できちゃうんだ。

つまり、

（頂点の数）×（頂点の数 – 3）÷ 2

ってことだね。

それじゃあ、

五角形の対角線の本数を求めてみよう。

公式のnに「5」を代入すればいいから、

n(n-3)÷2
= 5×(5-3)÷2
= 5

になるね。

た、たしかに対角線は5本ひけそう。。

す、すごいな。

この公式^^

なぜ多角形の対角線の本数の公式つかえるの？？

公式はめちゃ便利。

それはわかった。

だけれども、

なぜ多角形の対角線の本数を求められるんだろう？？

話がうますぎるよね。

つぎの3ステップで考えると、

公式をつかえる理由がわかるよ。

1. 「隣り合う頂点」と「自分」にはひけないから
2. それが頂点分ひける
3. 重なりを排除

Step1. 「1つの頂点から何本の対角線がひけるか？？」

1つの頂点から何本の対角線がひけるか

を考えてみよう。

まず、

隣りの2つの頂点

には対角線をむすべないよね。

むすぶと「辺」になっちゃう。

あと、自分には対角線ひけないよね？？

対角線をひくためには、

2つの頂点が必要だからね。

だから、

1つの頂点あたりn-3本の対角線

がひけることになるんだ。

だって、n個ある頂点のうち、

• 隣の2つの頂点
• 自分

の3つにはひけないからね。

これが公式の「n-3」の意味だよ。

Step2. 頂点の数だけひける

1つの頂点あたり、

「n-3」本の対角線がひける

ってわかったね？？

それじゃあn角形ならどうなるかな？？

n個の頂点があるから、

n(n-3)の対角線がひけそうだ。

だから、公式で(n-3)にnをかけているんだ。

Step3. 重なりをはぶく

最後はかぶりをはぶこう。

n角形のとき、

n(n-3)

の本数の対角線がひけそうってわかったね。

だけれども、

この本数にはかぶりがあるんだ。

なぜなら、

1つの対角線を2つの頂点でカウントしてるからね。

たとえば、五角形の対角線を考えてみよう。

下の緑の対角線をイメージしてほしい。

この対角線って、左の頂点1のときも数えているし、

右の頂点2のときもカウントしちゃっているんだ。

1本の対角線を2回ずつ数えていることになる。

だから最後に、

n(n-3)を2でわらなきゃいけないんだ。

どう？？

納得いったかな？？

まとめ：多角形の対角線の本数の求め方は公式をつかえ！

多角形の対角線の本数？？

そんなの簡単。

n(n-3)÷2

で計算してやろう。

公式をおぼえるのも大事だけど、

なぜ使えるのか？？

までおさえておこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。