三平方の定理(ピタゴラスの定理)の公式とは??
こんにちは!この記事を書いているKenだよ。電気最高。
中学3年生になると、
三平方の定理
を勉強していくよね??
この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、
ピタゴラスの定理
とも呼ばれてるやつね。
発見者の名前がついてるわけ。
この三平方の定理(ピタゴラスの定理)とは何かっていうと、
直角三角形の3つの辺の関係を表した公式
なんだ。
もうちょっと具体的にいうと、直角三角形には、
斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい
っていう関係があるんだ。
たとえば、斜辺の長さがc、その他の辺の長さがa・bの直角三角形ABCがあっとすると、
a² + b² = c²
っていう公式が成り立っているんだ。

たとえば、斜辺の長さが15cm、その他の辺の長さが12cm、9cmの直角三角形ABCをイメージしてみて。

斜辺ABの2乗は、
AB²=15² = 225
一方、その他の辺のBCとACの2乗して足してみると、
AC²+ BC²
= 12² + 9² = 144 + 81 =225
だね!
おっ。両方225になって等しくなってんじゃん!
ピタゴラスの定理の公式すごいな。。
>>三平方の定理(ピタゴラスの定理)の証明はこちら
三平方の定理(ピタゴラスの定理)の公式の何がすごいのか??
でもさ、
三平方の定理(ピタゴラスの定理)の公式のすごさがいまいちわからないよね??
ぜんぜん生活に役に立ったないじゃん!
って思ってない??
じつは、三平方の定理(ピタゴラスの定理)のすごいところは、
直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる
ってところなんだ。
たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。
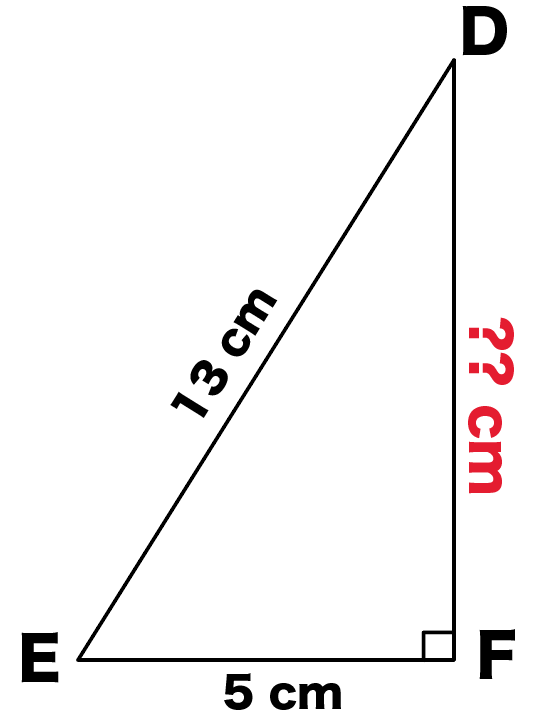
DFの長さって問題にも書いてないし、誰も教えてくれてないよね??
でも、大丈夫。
三平方の定理(ピタゴラスの定理)を使えば求められるんだ。
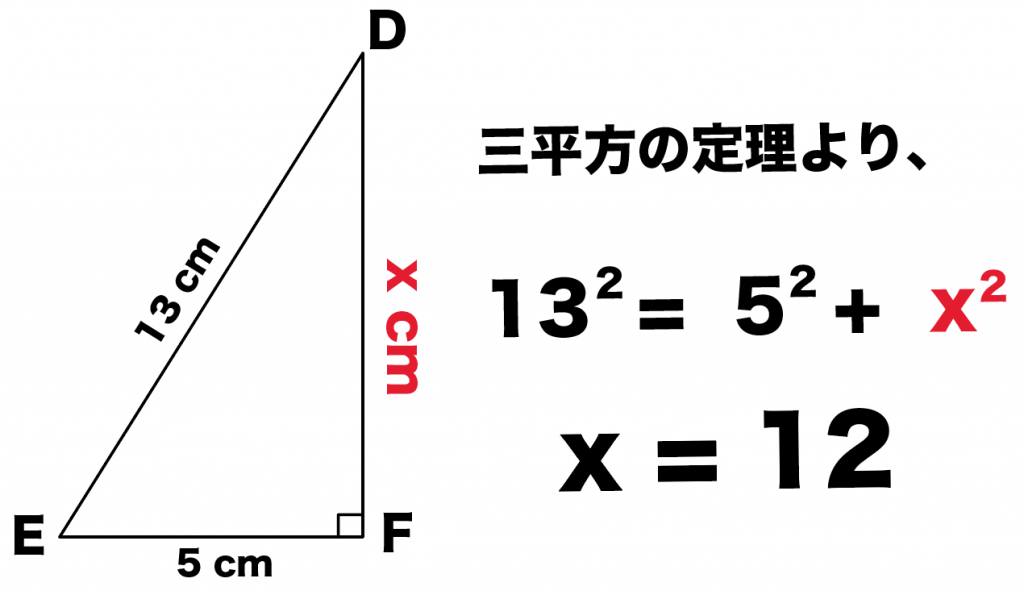
DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、
13² = 5² + x²
x = 12
あら不思議!
長さがわからない直角三角形の辺を求めることができたね。
>>三平方の定理(ピタゴラスの定理)の計算問題にチャレンジ!!
まとめ:三平方の定理(ピタゴラスの定理)の公式は便利だから絶対暗記!
三平方の定理(ピタゴラスの定理)の公式はめちゃくちゃ便利。
この公式なら、
だって計算できちゃうんだ。
入試問題や定期テストでむちゃくちゃよく出てくる定理だから、しっかりと覚えておこうね。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





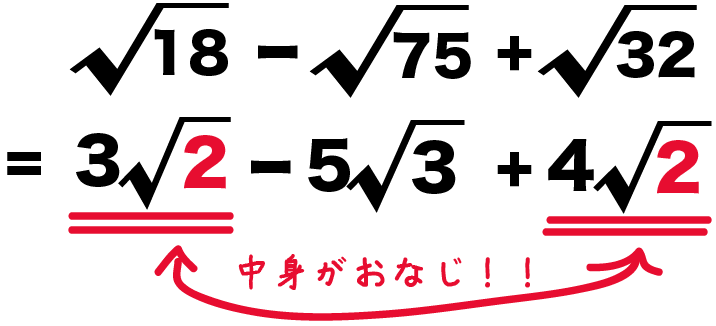
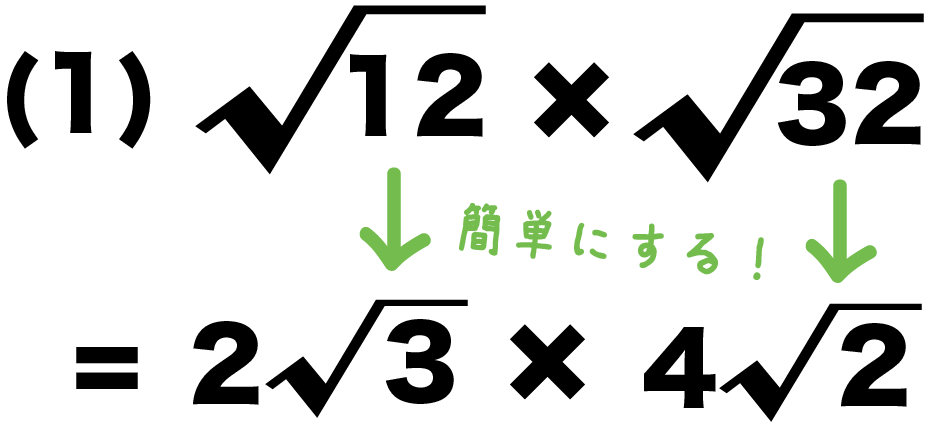


二乗の割り算ってどうやってやるんですか?
ルートの計算と同じですよ
x^2+2x-5<0の計算と解答を教えてください。
>x^2+2x-5<0
これは二次関数のグラフをかくといいね
周囲の長さが34メートル、対角線の長さが13メートルとするとき、長方形の2辺の長さは、どうやって求めるのか、教えてください。
>周囲の長さが34メートル、対角線の長さが13メートルとするとき、長方形の2辺の長さは、どうやって求めるのか、教えてください。
長方形の縦の長さをxメートル、横の長さをyメートルとしてみよう。
あとは
1. 周囲の長さに関する等式
2. 対角線の長さに関する等式
を2つ作ってxとyを求めよう!
平行四辺形の底辺?と対角線がわかっている時の面積の求め方を教えてください(°▽°)
>平行四辺形の底辺?と対角線がわかっている時の面積の求め方を教えてください(°▽°)
底辺を延長して、対角線が出てる1つの頂点から垂線を底辺の延長に下ろしてみよう!
延長した底辺の長さはどうなりますか?
Xの二乗=144はどうやって解けばいいんですか??
>Xの二乗=144
xは144の平方根になるね!
プラスマイナスの符号に注意!
こんにちわ、
長さを求めるとき、cos, sin やら√とか出てきますか?
>長さを求めるとき、cos, sin やら√とか出てきますか?
ルートは出てくるね!
なんで、
13の二乗=5の二乗+Xの二乗
X=12
になるんですか?
二乗の計算がよく分かりません。
初めまして
△ABCにおいて AB=3 AC=5 BAC=120° この時のBC の長さを求めるには 三平方の定理を使うんだと思いますが 図がないのでどれが斜辺になるのかわからなくて 公式がわかっていても足したらいいのかそれとも引いてのか判断出来ません><
押してください
>13の二乗=5の二乗+Xの二乗
指数の計算を復習しよう!
二乗だったら、その数を2回かければいいよ。
この二次方程式の場合、まずは指数を計算してから移行すれば解けるね
>△ABCにおいて AB=3 AC=5 BAC=120° この時のBC の長さを求めるには 三平方の定理を使うんだと思いますが 図がないのでどれが斜辺になるのかわからなくて 公式がわかっていても足したらいいのかそれとも引いてのか判断出来ません>< 補助線が必要になってくるね。 ABの延長線にCから垂線を引いてその交点をHとしてみよう。 まずは△ACHで直角三角形の比を使ってAHとCHの長さを出してみよう。 最後に△CBHで三平方の定理を発動させて斜辺BCを求めよう
底辺が8センチ 他の辺が4センチと4√2センチの三角形の高さの求め方を教えてください。
頂点から底辺に垂線を下ろしてみよう。
そしたら2つの三角形ができるはず。
高さをxとして、それぞれの三角形で三平方の定理を使って底辺をxで表してみよう。
あとはそいつらを足したら8cmになるっていう方程式作ればオッケー
2乗の意味がわからない。
(かずおさん)2乗とは、例えば
xの2乗=x×x
yの3乗=y×y×y
とか、指数?(数の右上についてるやつ)の数だけその数字をかけたものだとおもう…
小学生が理解する説明の仕方はどうすればよいでしょうか?
13² = 5² + x²
x = 12
パッと突然12と言う数字が出てきてますが、√144を素因数分解してるんですか?これ
確かに素因数分解してもいいな!
ただ、12²=144はよく出てくるから暗記しちゃうのも1つの手
Xの2乗の答えって何ですか?
9.8 mと8.2mの残りの一辺の長さ「三角形」
12m×15mの長方形の対角線の長さ教えてください。
三平方の定理が社会でどのように活用できるかを教えて欲しいです。
ひまわりさん、https://math.005net.com/yoten/2jihoteisiki.phpにいってみてください。2次方程式について解説されていますよ。(あくまでも、参考までに。求めていた答えと違っていても、あしからず。)
ピタゴラスの定理の証明の仕方はどうなんですか?