分数がふくまれる等式の変形はむずい??
こんにちは!この記事をかいているKenだよ。10円玉募金をはじめたね。
分数がふくまれる「等式の変形」ってむずかしいよね。
整数だけでもヤッカイなのに、分数がはいったらもっとヤバい。
そこで今日は、
「分数がふくまれている等式の解き方」をわかりやすく解説していくよ。
分数がふくまれる「等式の変形」には2つのパターンがあるんだ。
- 分母を払うパターン
- 通分するパターン
等式の変形の解き方1 : 「分母を払うパターン」
まず1つ目は分母を払うパターンだ。
これは「求める文字」が分子にあるタイプだね。
たとえば、
つぎの等式をaについて解きなさい。
a/2 + b/5 = 2
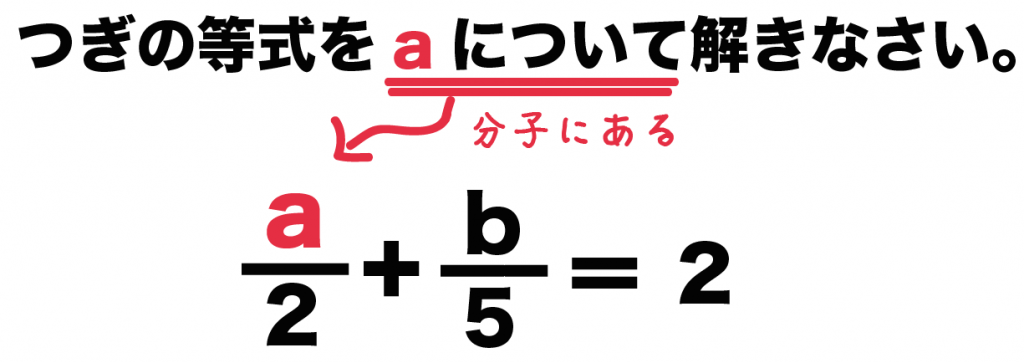
っていう問題だ。
これは、
○○について解きなさい
っていう○○の文字が分子にはいっているよね。
このタイプの問題はつぎの3ステップでとけちゃうんだ。
Step1. 分母をはらう!!
まず分母をはらっちゃおう。
等式から分数を消せちゃうってわけ。
つまり、
分母の最小公倍数を等式全体にかけてやればいいのさ。
例題でいうと、
分母の「2」と「5」の最小公倍数は「10」だよね。
こいつを等式の両辺にかけてみると、
10×(a/2 + b/5) = 2 × 10
5a + 2b = 20

になるね!
Step2. 「求める文字」を左に移項させるっ!
分母をはらった??
そのつぎは移項だね。
「求めたい文字」を左辺に移動させよう!
それ以外は反対の右辺におしこんでね^^
例題でいうと、
等式で求める文字は「a」だったよね??
ってことは「a」をふくむ項を左に、ソレ以外の項を右によせてやろう!
すると、
5a + 2b = 20
5a = 20 -2b
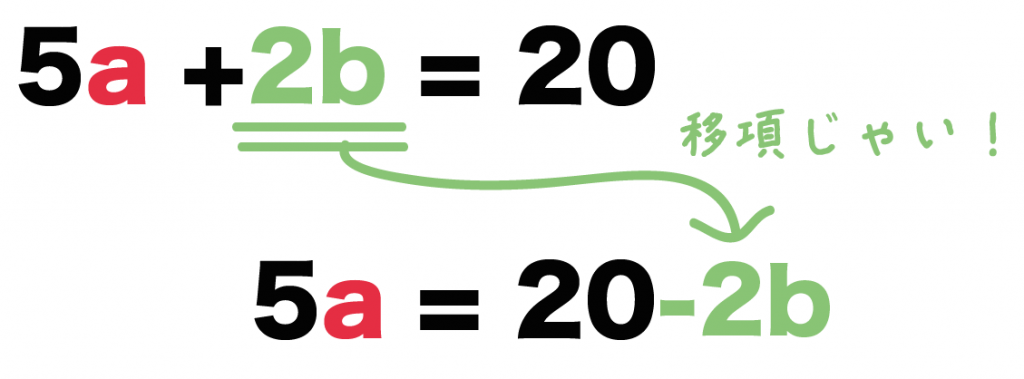
になるね!
移項するときに、項の符号が変わることに注意してね^_^
Step3. 求める文字の「係数」でわる!
最後は「求める文字」の係数をとってあげよう!
求める文字の前についている「数字」が係数だよ。
こいつで両辺をわってあげよう!
すると例題の式は、
5a ÷ 5 = (20-2b) ÷5
a = (20-2b)/5
になるね!
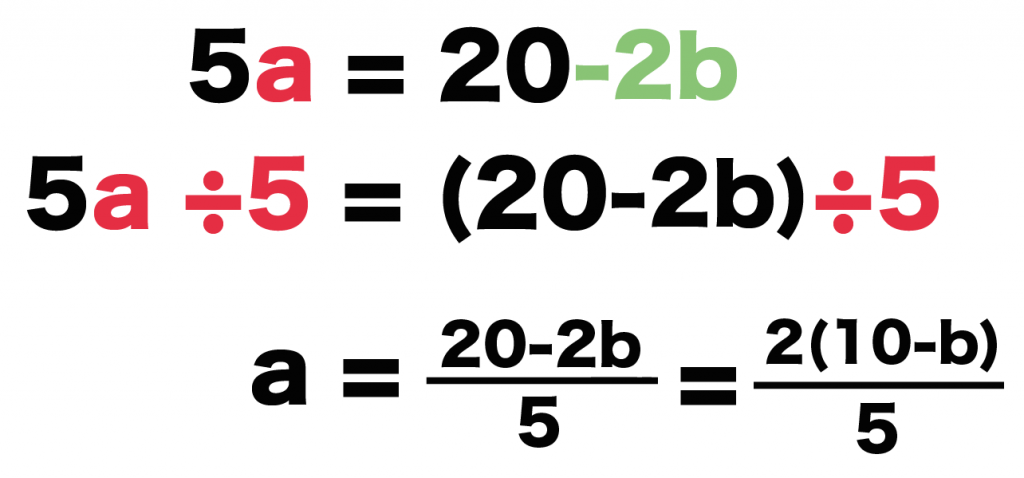
これで分母をはらうやり方はオッケーだね!!
等式の変形の解き方2:「通分するパターン」
等式の変形の2つ目のパターンは、
「求める文字」が分母にある場合だ。
たとえば次の問題のように、
つぎの等式をaについて解きなさい。
1/a + 1/b = 1/c
「〜について解きなさい」の「〜」が分母にはいっちゃっているパターンだ。
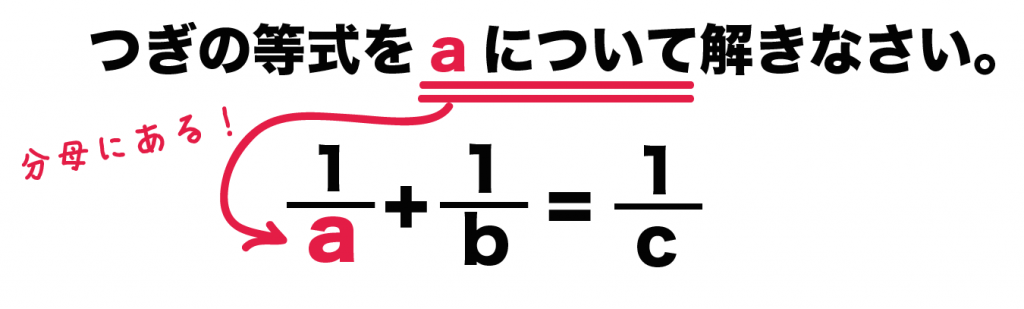
このタイプはつぎの3ステップでとけちゃうよ^^
Step1. 求める文字を左に移項するっ!
「求める文字」を左辺に、ソレ以外の項を右辺によせちゃおう!
符号に注意して移項しちゃってくれ!
例題の等式では「a」が求める文字だったよね?
だから「a」を左辺に、ソレ以外の項たちを右辺によせてみよう。
すると、
1/a = 1/c -1/b
になるね!
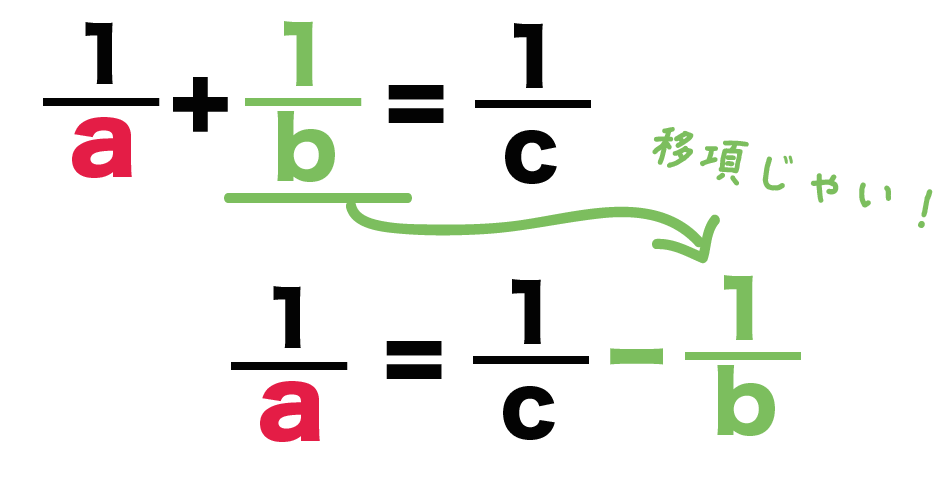
Step2. 右辺を通分するっ!
右辺を通分して1つの分数にしてみよう!!
例題でいうと、
1/c -1/b
っていう右辺を通分してやればいいんだね。
えっ。通分のやり方がわからない!?
そんなときは「分数をふくむ文字式の通分方法」を復習してみてね^^
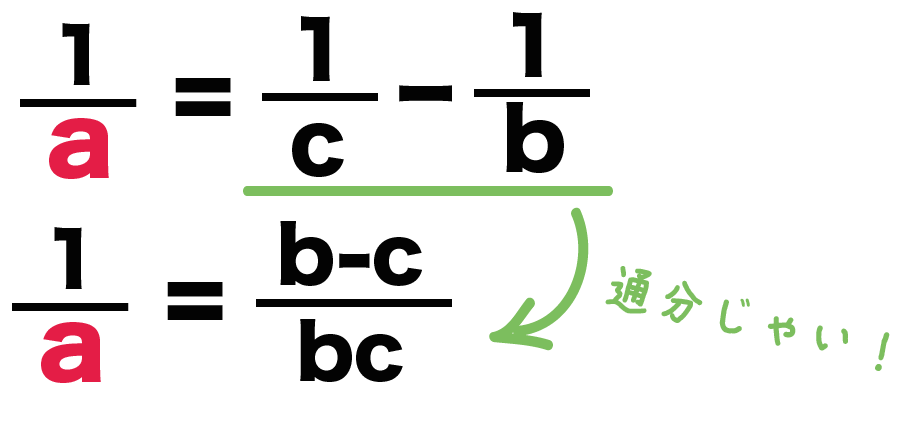
通分してやると、
(b-c)/bc
になるね!
Step3. 両辺を逆数にするっ!
いよいよ最後のステップ。
両辺の分数を逆数にしてあげよう!!
左辺と右辺はそれぞれ1つの分数になっているから、
分子と分母を入れ替えてやればいいのさ。
例題でいうと、
1/a = (b-c)/bc
a = bc/(b-c)
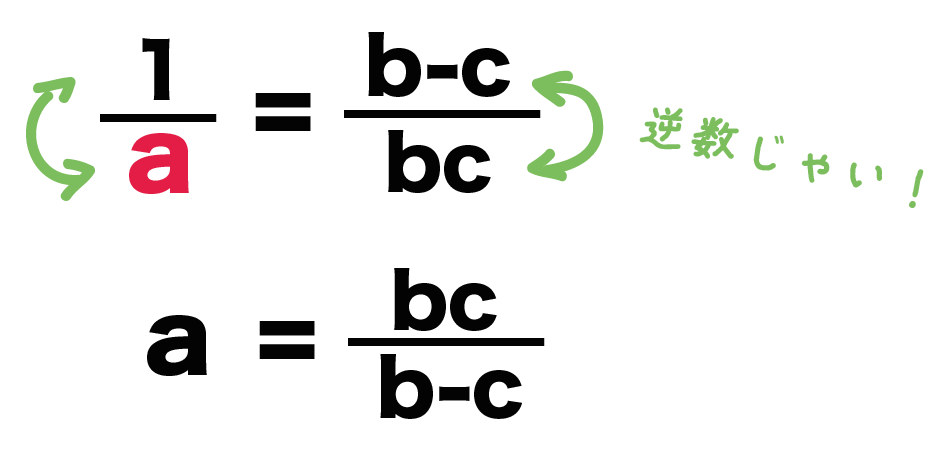
になるね!
これで「通分するパターン」の解き方もマスターしたね。
おめでとう!
まとめ:分数がふくまれている等式の変形は2つ解き方だけ!
分数がふくまれている等式の変形のやり方はどうだった??
- 分母をはらうパターン
- 通分するパターン
をマスターしておけば大丈夫。
きっとテストでいい点とれるはず!本番前によーく復習しておいてね^^
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。



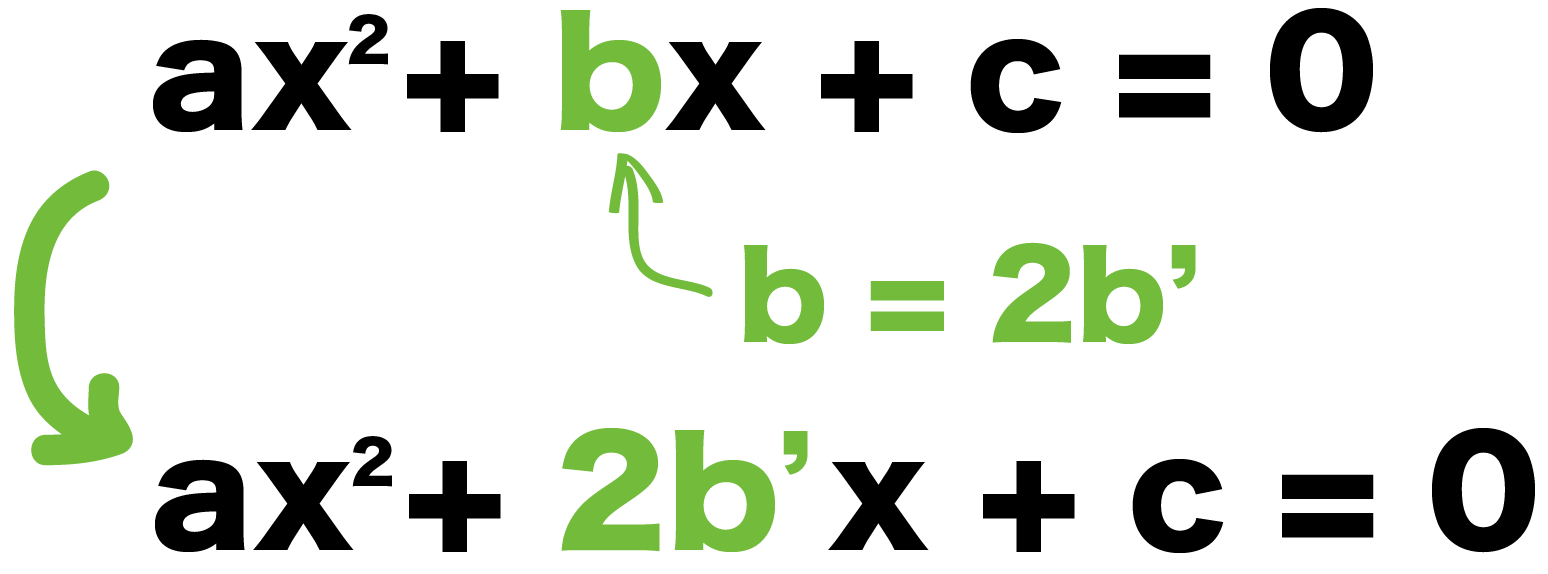



2a-C=b/3 ( a )
の場合どうすればいいのですか?
S=1/2ah(h)の解き方教えてください。
m=1/2(x+y) (x)
というようにXを解く場合はどうしたら良いのでしょうか?
まず分母払ってみよう!
分母の数を左辺と右辺にかけてみて!
分母払っちゃうとわかりやすいかな!
2ahを両辺にかけてみて
分母を払ってみよう!
中3数学因数分解の超難問ありませんか?
a+b/x+y=3/4[a]
>a+b/x+y=3/4[a]
どっちが分母かわからんけど、分母の数にaがあるんだとしたら、
両辺に分母の数をかけて分数を消し去ろう!
x/30―20/60=x/48+10/60
お願いします…
>x/30―20/60=x/48+10/60
分母の最小公倍数をかけてやろう。
この場合だと、240になるのかな
x²=aの2乗+bの2乗-2abcのときの、cについて解くという問題があるのですが、どうやって解くのですか。教えてください。
>x²=aの2乗+bの2乗-2abcのときの、cについて解くという問題
aの2乗+bの2乗を左辺に移行して、最後に-2abで両辺を割ってみよう!
y=3/4 -½
Yを変形して
3X-4Y-2=0
になる理由を教えてください
>y=3/4X -½
Yを変形して
3X-4Y-2=0
になる理由を教えてください
両辺に分母の最小公倍数4をかけて移項してるね
C=2分の1(a+3b)〔a〕 教えてください!!
>C=2分の1(a+3b)〔a〕
両辺に2をかけて分数を消してみよう。
あとはa以外の項を逆側に移項してaを1人にしてみよう
2分aは、全部に2をかけてa=になってもいいですか?
458=48/48+x *100
>2分aは、全部に2をかけてa=になってもいいですか?
いいよ!
両辺に2をかけるのを忘れずに
>458=48/48+x *100
両辺に分母の(48+x)をかけて
分数をけしさろう
2分のa+b=bcをbについて解く問題の答えが
b=2c-1になるのはどうしてですか?
>2分のa+b=bcをbについて解く問題の答えが
b=2c-1になるのはどうしてですか?
両辺に2をかけてまずは分数を消し去ろうぜ
x-y分のz=tをyについて解く問題のやり方を教えて下さい
>x-y分のz=tをyについて解く問題のやり方を教えて下さい
両辺にyをかけてみるとスッキリするよ〜
30=E/R+r (R)
( )内の文字についてとけ
といつ問題なんですが
答えがR=1/30(E-30r)
で自分が何度やってもR=E/30rで答えが合いません
どうやってとくんですか
教えて下さい。
>30=E/R+r (R)
分母を両辺にかけて分数を消し去ろう
F=T/W-Rが(F+R)W=Tになり、W=T/F+Rとなる意味がわかりません。おしえてください。
>F=T/W-Rが(F+R)W=Tになり、W=T/F+Rとなる意味がわかりません。おしえてください。
分母のWを両辺にかけてみるといいよ〜
5.1=100/( x/2+(100-x)/15)
x=29.9になる解き方を教えて下さい。
>5.1=100/( x/2+(100-x)/15)
分母数を両辺にかけて分数を含む形を崩してみよう!
さすれば解きやすくなるはず
y=2x-1/3x-2とかの場合はどうするんですか(xについてときます。)
>y=2x-1/3x-2とかの場合はどうするんですか(xについてときます。)
分母は3x-2かな?
その場合、分母の3x-2を両辺にかけて分数を消し去ろう。
あとはxの項を左辺に、それ以外を右辺に移行して最後にxの係数で両辺を割ってやるといいよ〜
a=3/b+2c bについて とは、どうしたらいいでしょうか
>a=3/b+2c bについて とは、どうしたらいいでしょうか
右辺の分母は3ってことかな?
だとしたら両辺に3をかけて分数を消し去ろうぜ
x
– + 3y = 2 (x)
4
ってどうやって解きますか?
>x
– + 3y = 2 (x)
4
分数がうざいから分母の4を両辺にかけてみよう。
あとはいつも通りとくだけ
c=1/2(a+3b)と
m=a+b+c/3の
解き方を教えて下さい
何について解くのかによるな!
m=a+b+c/3の aについての
解き方を教えて下さい
s=さんぶんのいちah(a)が解けません。
分母の数を両辺にかけて分数を消し去ろう!
v=1/3πrの二乗hで、hを求めるにはどうしたらいいですか?
まず分数がうざったいな!
両辺に3をかけて消し去ろう
62.5=10/x ✕ 100
という問題で頑張って調べたら分母のxを移行するって書いてあったんですがなぜ移行できるのですか?そして答えは16になりますか?
分数が含まれる方程式の場合、分母を両辺にかけて分数を消すといいな!
分母がxだったら両辺にxをかけてみよう
こんにちは勉強苦手な者です。
10円玉募金、僕も始めました‼
等式の変形はとても難しい問題だと思っていました。
でもkenさんの説明のおかげで分かるようになりました‼
kenさんのおかげで勉強が少し好きになりました‼
良かったら返信お願いします。m(__)m
b=5/2a+3の解き方教えてください