【中学数学】平均値と中央値の3つの違い

平均値と中央値ってどう違うの？？

こんにちは！この記事をかいているKenだよ。ほうじ茶しみるわ。

資料の活用を勉強していると、

• 平均値
• 中央値

っていう代表値を勉強するよね！

求め方はマスターした。

だけど、

平均値と中央値はどう違うんだろう？？

って思わない？

名前も似てるし、

漢字3文字だし^^;

今日は平均値と中央値をごちゃまぜにしないために、

平均値と中央値の3つの違い

を解説していくよ。

よかったら参考にしてみて^^

平均値と中央値の3つの違いとは？？

平均値と中央値には3つの違いがあるよ。

1. 求め方
2. ぶれにくさ
3. 求めやすさ

砲丸投げの例で解説していこう。

違い1. 　出し方・求め方がちがう！

平均値と中央値は求め方がちがうよ！

求め方・出し方は、

• 平均値：（データの合計）÷（データ数）
• 中央値：　大きい順にならべたときの真ん中のデータ

だったよね？？

砲丸投げの例をみてみよう。

この10人の平均値は、

（10人の平均値）＝（データ合計）÷（データ数）
＝　(7 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 + 7 ) ÷ 10
＝　6.8

になる。

じゃあ、中央値はどうなの？？

中央値はまず、大きい順にデータを並び替えて、

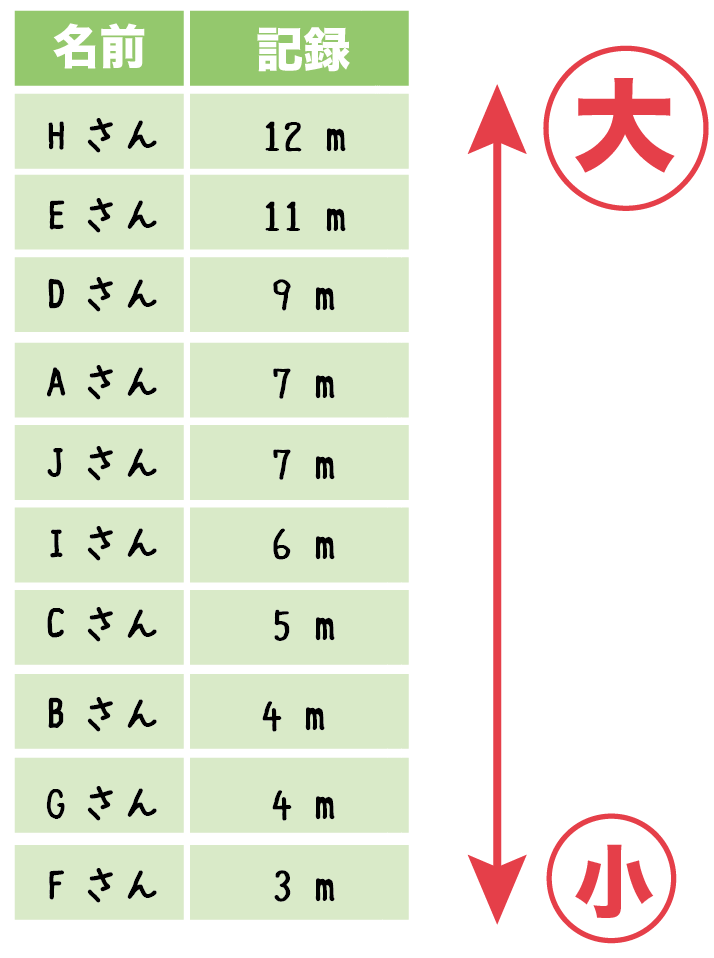
真ん中のデータをさがせばいいんだ！

この例ではデータ数は偶数。

真ん中2つのデータの平均をとってあげると、

（中央値）＝　（真ん中1 + 真ん中2）÷ 2
＝　（7 + 6）÷ 2
＝　6.5

になるね。

中央値と平均値では出し方がちがう

ってことを覚えておこう^^

違い2. ぶれやすさがちがう！

平均値と中央値には、

ぶれにくさいに違いがあるよ。

データの中にとびぬけて変わったデータがあるとき、

影響の受け方がちがうんだ。

• 平均値：　変なデータの影響をうけやすい
• 中央値：　変なデータの影響をうけにくい

たとえば、砲丸投げの例をかんがえてみよう。

よくありがちなことだけど、Aさんがいきなり覚醒したとしよう。

この日は覚醒しすぎて、宇宙記録の100mをたたき出しちゃったらしい。

このとき、平均値と中央値はつぎのように変化しちゃうんだ。

• 平均値：　6.8 → 16.1
• 中央値：　6.5 → 6.5

ね？

中央値はぜんぜん変わらないけど、

平均値はむちゃくちゃ変化してるっしょ！？

こんな感じで、

特殊なデータからうける影響の大きさが違う

ってことをおぼえておこう。

違い3. 求めやすさがちがう！

3つめの違いは、

平均値と中央値の求めやすさが違うってことだ。

じつは、

データ数の多さによって求めやすさが違うんだ。

平均値は求めやすさは変わらない。

だけど中央値は、

• データ少ない →  超求めやすい
• データ多い　→　求めにくい

と性質が変化するんだ。

たとえば砲丸投げの例でみてみよう。

たとえば、チャレンジャーがEさん・Dさん・Hさんの3人のとき。

このときの中央値は1秒で求められる。

だって、3つしかデータないし、

データ数が奇数だからね。

真ん中の11mが中央値さ。

逆に、チャレンジャーが増えすぎた時はどうかな？？

Aさん〜Zさんまでの26人が参戦したとしよう。

このとき、中央値を求めるのはダルいね。

なぜなら、

• データを並び替える
• データ数が奇数か偶数か調べる

っていう作業がめんどうだからね。

データ数が少ないときはいいんだけど、

増えすぎると大変になっちゃうんだ。

こんな感じで、

データ数の多さにより平均値と中央値のだしやすさが違う

ってことをおぼえておこう^^

まとめ：平均値と中央値はぜんぜんべつもの！！

平均値と中央値はまったくべつもの。

漢字とか雰囲気とか似てるけど、

• 求め方
• ぶれにくさ
• もとめやすさ

という3点で違うよ。

テスト前に復習してみてね。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。