【ルート計算】展開公式をつかう3つの平方根問題の解き方

ルート・平方根で展開公式はつかえるの？？

こんにちは、この記事をかいてるKenだよ。ワッフルにもいろいろだね。

平方根の計算問題をたくさんといてきたね。

たぶんね、これからもルート計算をガシガシやっていくよ。

悲しいけどこれが現実だ。

んで、その計算問題のなかには、

展開公式をつかう問題

がでてくると思うんだ。

えっ。

展開の公式なんて忘れてたって？！？

ノンノン。

展開公式にはつぎの3つがあったよね。

1. (x+a) (x+b)の展開
2. 平方の公式
3. 和と差の積

こいつらは平方根の計算式につかってもOK。

むしろ、ガンガン使って欲しいね。

今日は、

3つの展開公式を使った平方根の計算問題をといていこう！

=もくじ=

• 展開公式をつかう問題の基本
• 3つのルート計算問題

ルートの式に展開公式をつかう問題の解き方

展開公式をつかう問題はシンプル。

つぎの2ステップでとけちゃうよ。

1. 展開公式をつかう
2. ルートの足し算・引き算する

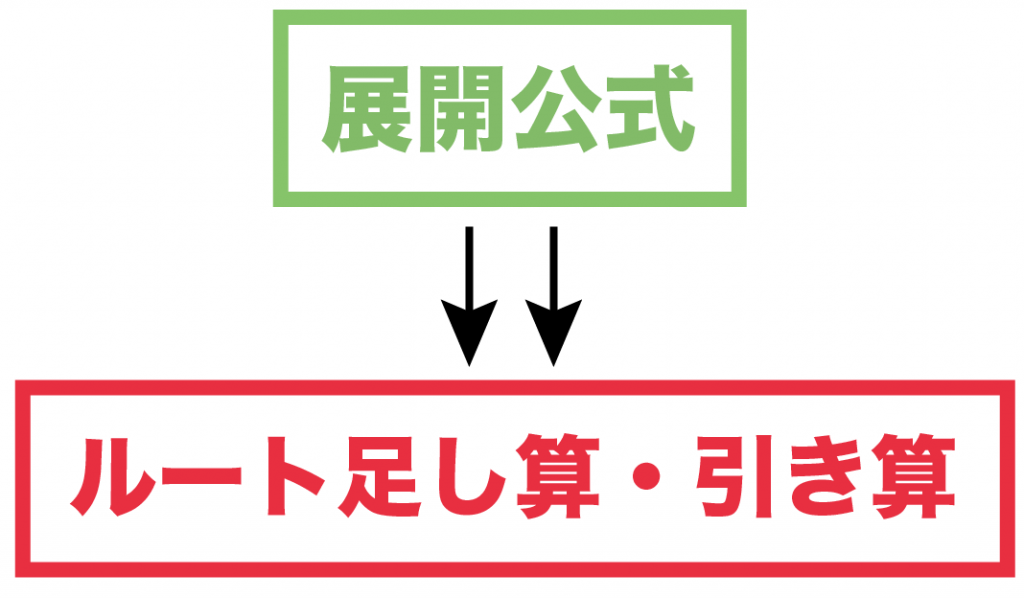
ようするに、展開公式で簡単にして、いつも通り計算ってわけだ。

今日は展開公式を3つ使ってみよう^^

1. (x+a) (x+b)の展開
2. 平方の公式
3. 和と差の積

問題1. 「(x+a)(x+b)の展開」

まず展開公式1つめの、

(x+a)(x+b) = x^2 + (a+b)x + ab

をつかおう。

たとえば、つぎのような計算問題だ。

練習問題

つぎの平方根の計算をしなさい。

( √5 – √2 ) (√5 + √3 )

この計算式では、2つの（）のなかに、

√5

があるよね？？

で、そいつらに、

• -√2
• √3

がそれぞれ足されてる。

ってことは、展開公式でいうと、

• x = √5
• a = -√2
• b = √3

になってるわけさ。

(x+a)(x+b)の展開公式をつかうと、

( √5 – √2 ) (√5 + √3 )
= √5^2 +√5 (-√2 + √3) – √6
= 5 -√10 + √15 – √6

になるね。

さてと・・・ルートの足し算をっと・・・

っていいたいところだけどね、これ以上計算できないんだ。

なぜなら、

ルートの中身がぜんぶ違うからね。

これで計算終了だ！

問題2.  「平方の公式」をつかう

おつぎは平方の公式の、

(a+b)^2 = a^2 +2ab + b^2

をつかってみよう。

つぎの例題をといてみて。

( √5 – √2 )^2

平方の公式で展開すると、

( √5 – √2 )^2
= ( √5 )^2 – 2×√5 × √2 + (√2 )^2
= 5 -2√5 +2

になる。

あとはルートの足し算・引き算するだけ。

数字同士でまとめると、

( √5 – √2 )^2
= ( √5 )^2 – 2×√5 × √2 + (√2 )^2
= 5 -2√5 +2
= 7 -2√5

になるね。

これで計算終了だ^-^

問題3. 「和と差の積」をつかう

最後は、和と差の積の公式をつかってみよう。

(a+b)(a-b)  = a^2 – b^2

つぎの計算問題をといてみよう。

練習問題3.

つぎの平方根の計算をしなさい。

( √5 + √2 ) (√5 – √2 )

公式にあてはめると、

• a = √5
• b = √2

になるはずだ。

なぜなら、

2つの（）に√5があって、√2は符号違いだからね。

和と差の積の公式で計算すると、

( √5 + √2 ) (√5 – √2 )
= ( √5 )^2 – ( √2 )^2
= 5-2

になるね。

あとはルートの足し算・引き算だ。

この計算式だと、ルートもくそもない。

整数同士で計算してやると、

( √5 + √2 ) (√5 – √2 )
= ( √5 )^2 – ( √2 )^2
= 5-2
= 3

になるね！

これで計算終了だ^^

まとめ：ルートの計算式だろうが展開公式つかおうぜ！

平方根の式に展開公式つかえたかな？？

1. (x+a) (x+b)の展開
2. 平方の公式
3. 和と差の積

を使い分けよう。

あとは、問題演習あるのみ。

展開しまくっていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。