一次関数で垂直な直線の式を求めたい!
前回、「平行な2直線の求め方」を勉強してきたね?
今回はそれと似たようなやつで、
ある直線に「垂直な」式を求める問題
にチャレンジしよう。
例えば、次のような問題↓
状況を図にかくとこんな感じ。
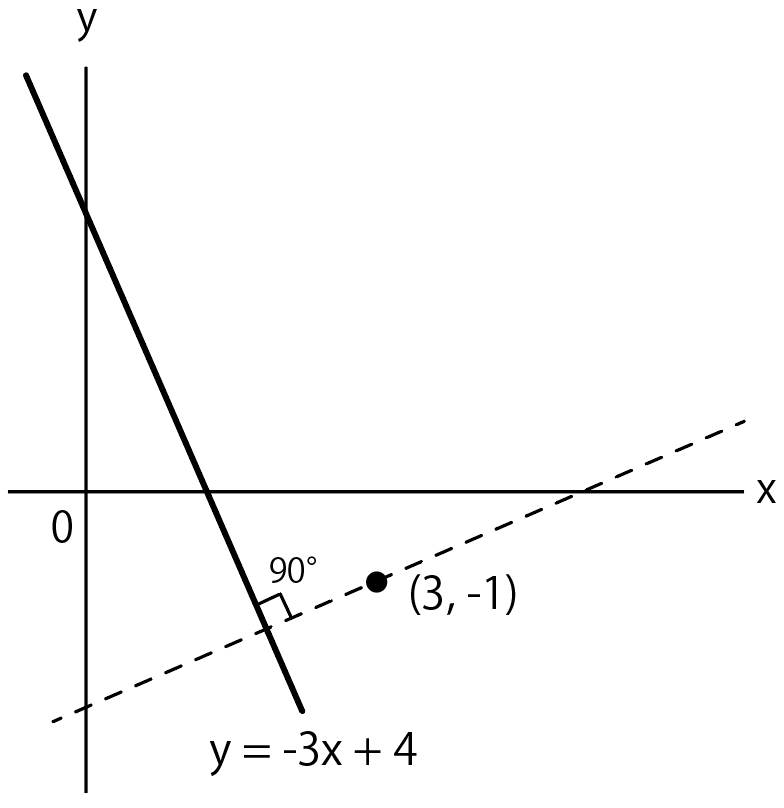
点線になっている一次関数の式を求めるんだ。
この手の問題は次の方法で解けるはず。
Step1. 傾きを求める
2直線が垂直だったらわかること。
それは、
2直線の傾きをかけたら 「- 1」になる
こと。
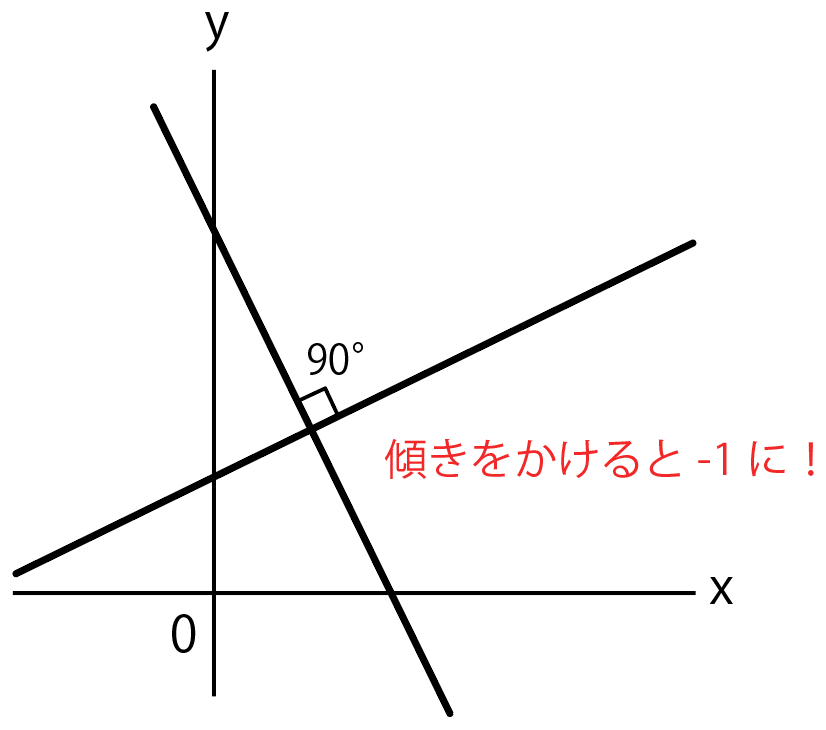
例えば「$y = – 3x + 4$」に垂直な直線の傾きを考えてみよう。
傾き「- 3」にかけたら 「- 1」になる傾きを求めればいいんだ。
求めたい直線の傾きを「a」とすると、
$$- 3 a = -1$$
$$a = \frac{1}{3}$$
と出てくるね。
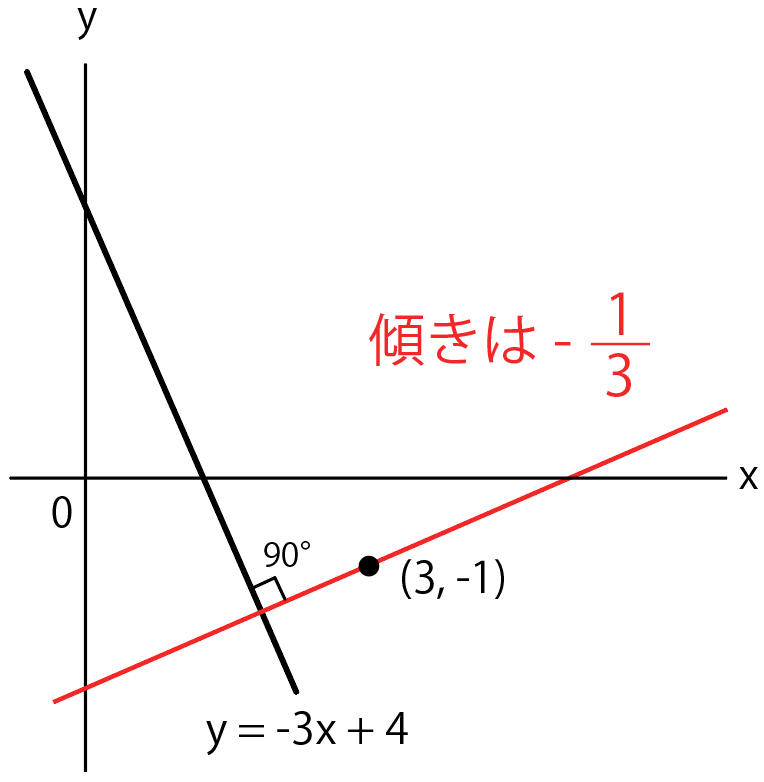
って感じで、垂直ってヒントから、一次関数の傾きがわかっちまうんだ。
Step2. 座標を代入する
さっきのステップで$y = ax + b$の傾きが分かった。
あとは座標を代入して「切片b」を求めよう。
例題では
点(3, – 1)を通る
っていうヒントがあったから、この座標を代入しよう。
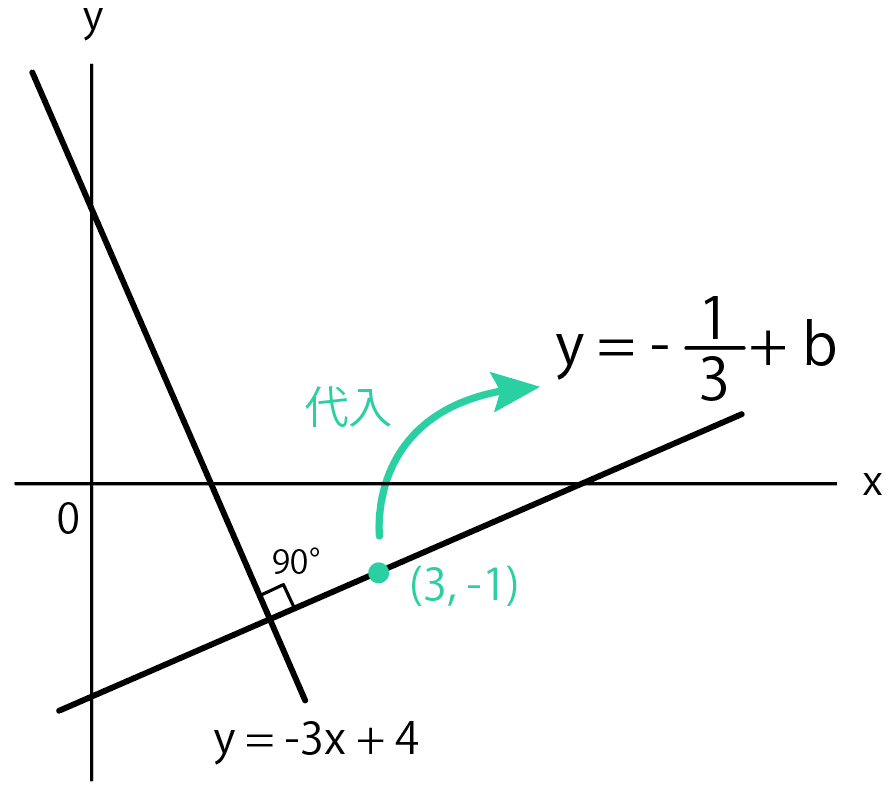
すでに傾きは$\frac{1}{3}$とわかったから、
$$y = \frac{1}{3} x + b$$
$$-1 = \frac{1}{3} × 3 + b$$
$$b = -2$$
となるね。
なぜ傾きをかけたら「- 1」になるのか?
ここで疑問に思うのが、
垂直な2直線の傾きをかけたらなぜ「- 1」になるのか?
ってこと。
シンプルでわかりやすいけど、理由を教えてもらえないとしっくりこないよね。
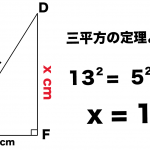
これを証明するには、中学3年生でならう三平方の定理を使うよ。
例えば$y =mx$、$y = nx$という1次関数(比例)があったとしよう。
そして、直線上にx座標が「1」の点A、Bがあるシチュエーションを想像してくれ。
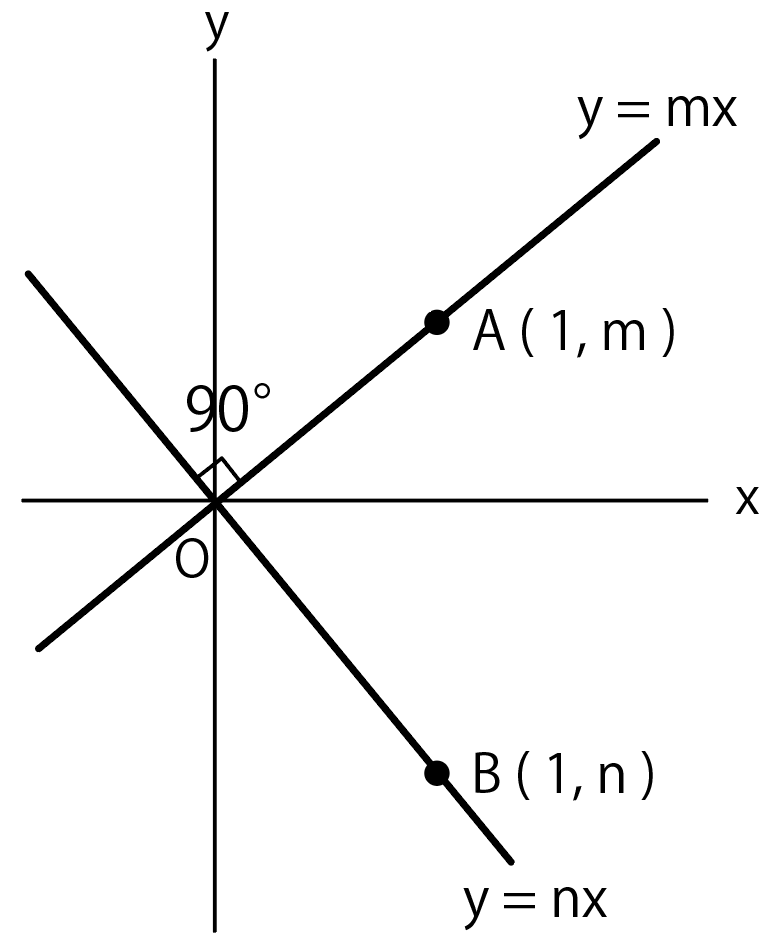
このとき、ABの長さはAのy座標からBのy座標を引いて
$$m – n$$
になるはず。
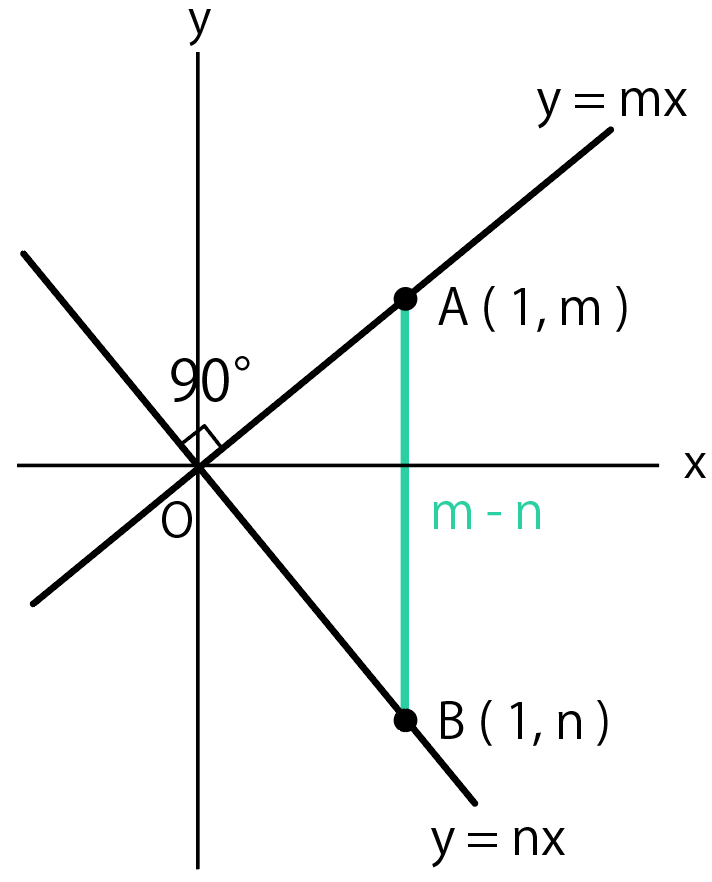
三平方の定理を使うと
$$OA =\sqrt{(1² + m²)} $$
$$OB = \sqrt{(1² + n²)}$$
と計算できる。
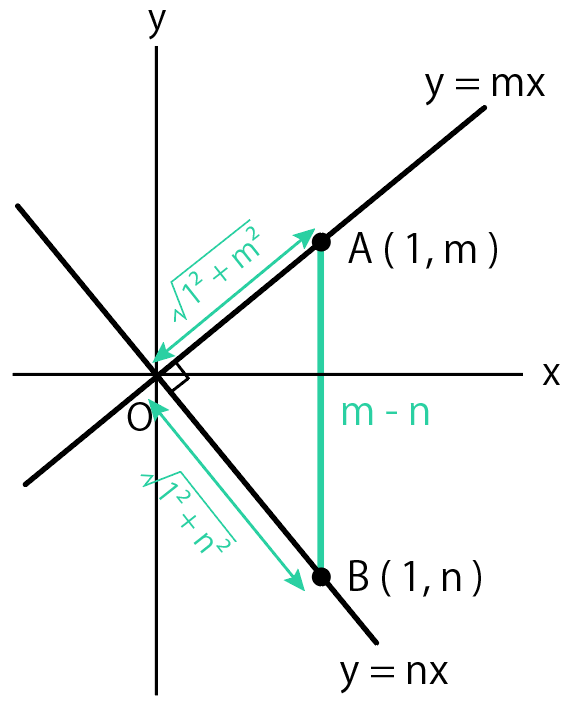
直角三角形OABに注目して、三平方の定理を使うと、
$$AB² = OA² + OB²$$
$$(m – n)^2 = {\sqrt{(1² + m²)}}^2 + {\sqrt{(1² + n²)}}^2$$
$$2mn = -2$$
$$mn = -1$$
となる。
「m」と「n」は垂直な直線の傾きだから、
垂直な2直線の傾きをかけると-1になる
って証明できるね。
こんな感じで、垂直な直線の傾きをかけると -1 になるから便利。
ついでに、なぜそうなるのかを理解しておけば怖いものなしだ。
テストに出てきやすいからよーく復習しておこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






直線Mの式の求め方が分かりません
一次関数の問題で、時間を求める文章題(○時間○分○秒とか・・・)求め方を教えて下さい。
y=-1/3X+bと記載されていますが、y=1/3X+bの間違いですよね?
これは一回一回証明しなくても他の証明問題で使っていいのか?
特に高校入試の証明問題の記述とか。