平行な直線の式を求めろ・・・・だと?
一次関数でわりと出てくるのは
平行な直線の式を求めよ
ってやつ。
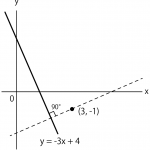
例えば次の問題↓
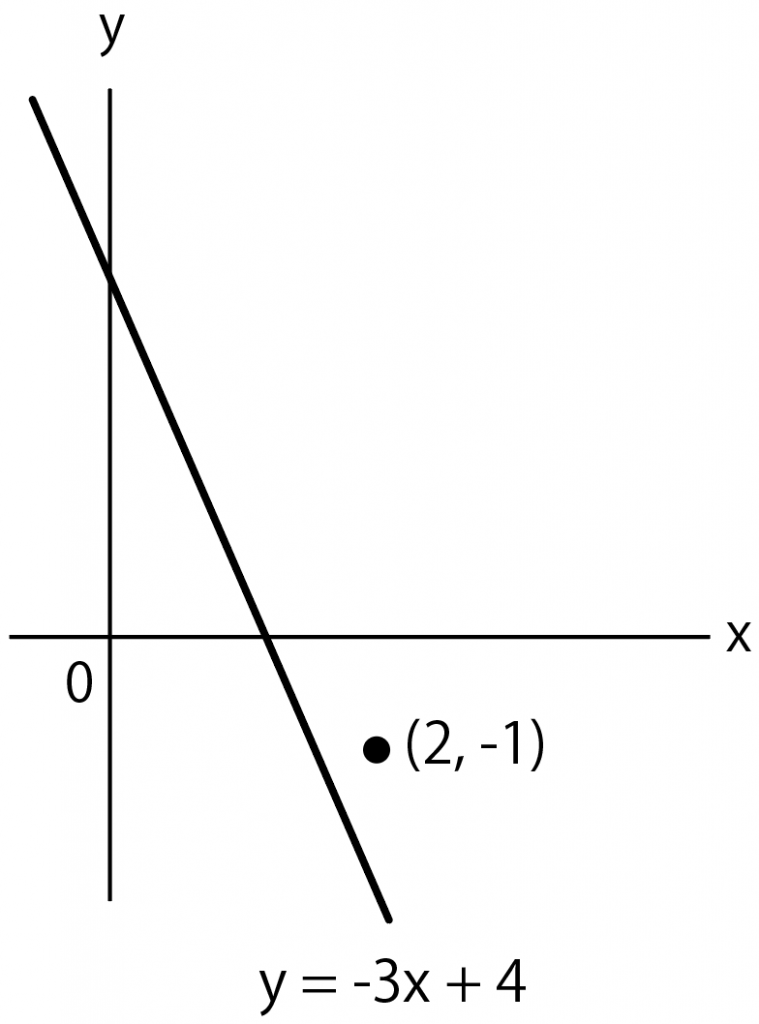
よく出てくるわりに、解き方がワンパターン。
1度解けるようになれば大丈夫。
「傾き」を求める
一次関数の「傾き」から求めよう。
問題文でわかっているのは
「とある直線」と平行
ってこと。
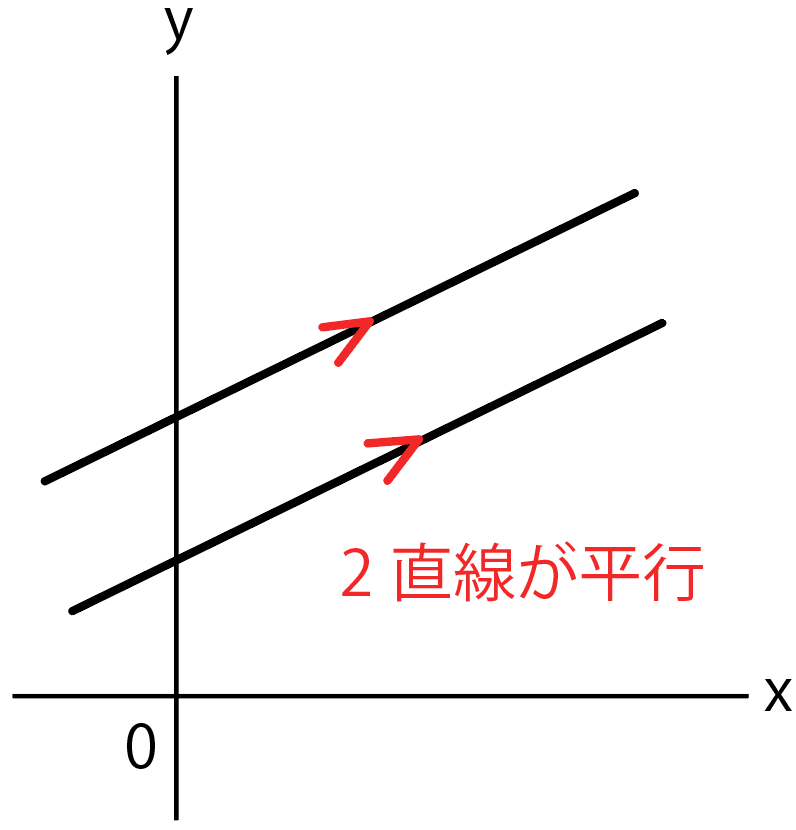
2直線が平行だとわかることが1つ。
それは、
傾きが等しい
ってこと。
一次関数の「傾き」とは、変化の割合のことで、
xが1増加したとき y がどれぐらい変化するか?
を表していたね。
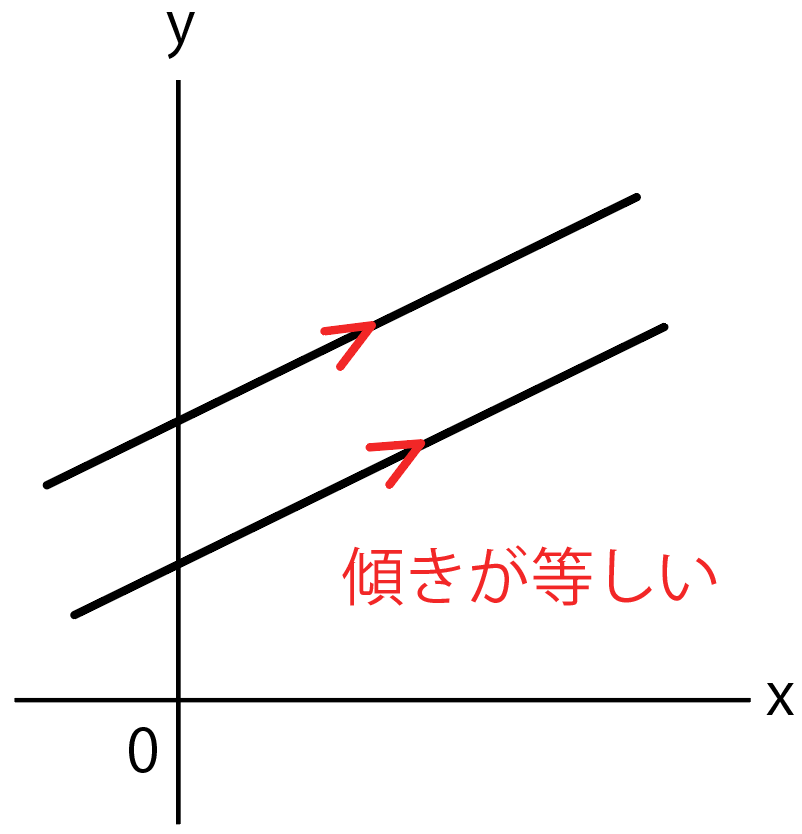
2つの直線が平行ってことは、
xが1変化した時の y の変化量も同じであるはず。
変化の割合(傾き)が違っていたとしたら、平行ではなく、どっかしらで交わっちゃう。

よって、平行な2直線の傾きは等しいはずだね。
例題では
直線 y = – 3 x + 4 と平行
って言ってるから、求めたい傾きは、 y = – 3 x + 4 の傾き「-3」と等しいはず。

一次関数 y = ax + bの傾き「a」が「-3」ってことだから、
y = -3x + b
になる。
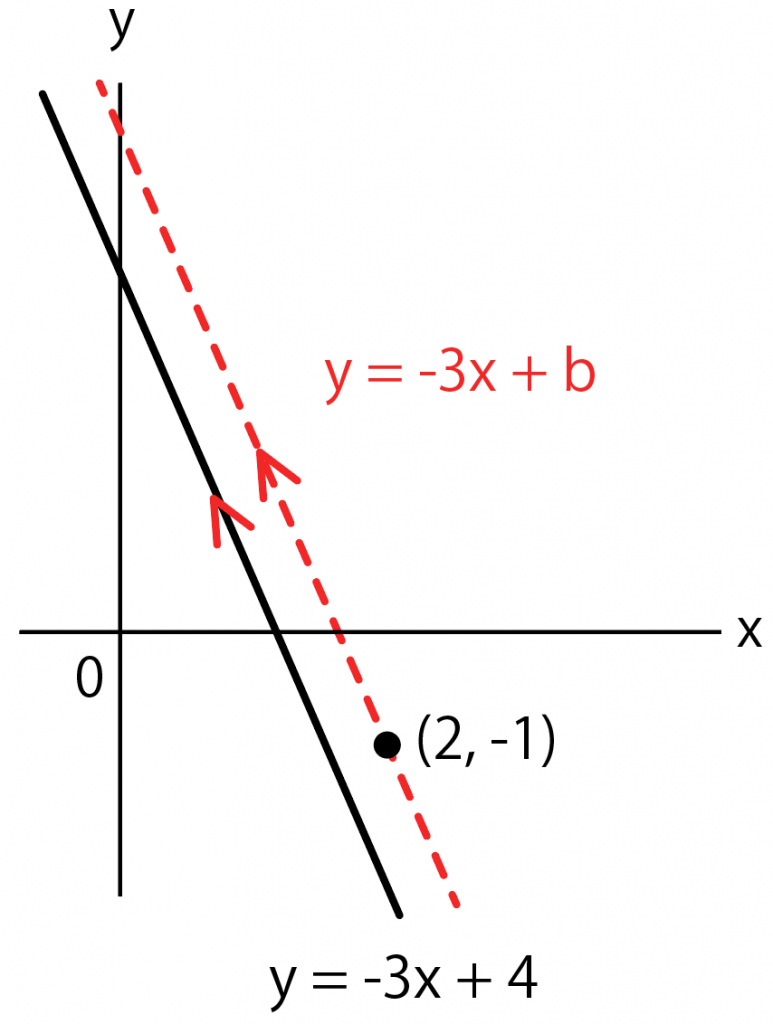
座標を代入
これでステージクリアにしたいけど、まだ解けたことにならないよ。
なぜなら、一次関数y =ax + bのうち、切片「b」が不明だからさ。
bの正体をつかんだらはじめて、直線の式が求められたことになる。
ってことで、切片bを求めるため、座標を直線の式に代入しよう。
例題だと、
y = -3x + b
に
点(2, -1)
という座標を代入するんだ。

すると、
y = -3x + b
-1= -3 × 2 + b
b = 5
になる。
つまり、切片bは「5」だから、直線の全体の式は、
y = -3x + 5
になるはず。
こんな感じで、
「2直線が平行」 → 「傾きが等しい」
を知っていれば難しいことはないね。
次は「垂直な2直線の式の求め方」を勉強していこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。








右平行式
直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる直線の式を求めろ
垂直の直線はどうやってやるのですか?
y=ax+bとy=axのグラフを比較し、その内容をまとめよう。
というような問題が出たらどう答えればいいですか?
直線y=3x +2とy軸上で交わる、というような問題はどうやって解くのでしょうか
直線y=ax+bに平行で、直線y=ax+bとy軸上で交わる直線の式ってどうやって求めるんですかね。
解説お願いします!(*- -)(*_ _)ペコリ
アザス
いつも分かりやすいです。有難う御座います(^ ^)
いつもわかりやすい説明をありがとうございます。(^○^)
これからも応援しています。(質問じゃないけど)