【等積変形】三角形の問題がわかる5つのステップ

等積変形の三角形の問題を攻略したい！

こんにちは！この記事をかいているKenだよ。チョキはすごいね。

等積変形の問題は大きく分けると、

• 三角形の作図問題
• 四角形の作図問題

の2つある。

どちらも等積変形をつかうのは同じ。

だけど、

びみょーに解き方がちがってくるんだ。

せっかく勉強するんなら、どちらの解き方もマスターしておきたいね。

そこで今日は、

等積変形の「三角形」の問題をいっしょにといてみよう！

等積変形の「三角形」をつかった作図問題

等積変形の三角形の問題は、つぎのようなやつだね↓↓

この手の問題の解き方はシンプル。

三角形を等積変形して、

そいつの面積を二等分する線をひけばいいんだ。

つぎの6ステップでとけるよ。

1. 底辺を延長しまくる
2. 点と対角をむすぶ
3. 平行線をかく
4. 等積変形する
5. 垂直二等分線をかく
6. 交点をもとめる

コンパスと定規で攻略していこう！！

Step1. 底辺を延長しまくる

三角形の底辺を延長しよう。

好きなだけ延長していいよ。とくべつにね。

できるかぎり左右にのばしてみて。

例題でいうと、底辺はBCだね。

こいつを横に延長してやると、こうなるね！

えっ。

かっこわるいって！？

そうだね。

でもここからが等積変形の面白いところなんだ^^

Step2.　点と対角をむすぶ！

「中点を通る点」と「対角」をむすんでやろう。

例題でいうと、点Pと点Bだね。

こいつらを定規ですーっと結んでやると、

こうなる！

Step3. 平行線をかく！

頂角を通る平行な線をかいてみよう。

ここでも定規が活躍するよ。

例題でいうと、

点Aを通ってBPに平行な直線ってわけだ。

せっかくだから、

底辺との交点をDとしよう！

Step4. 等積変形する！

等積変形で「面積の等しい三角形」をつくっちゃうおう。

具体的にいうと、

新しくできた底辺との交点

と

二等分線が通る点

を結べばいいんだ。

例題でいうと、点DとPを結べばいいね。

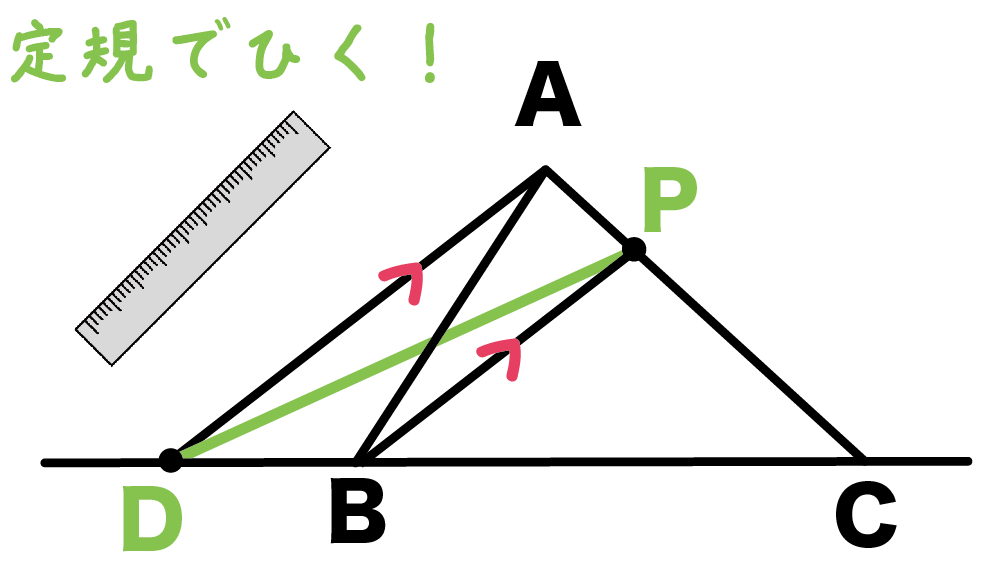
えっ。どこが等積変形になってるのかッテ？！

じつは、これ、

△ABP = △DBP

になってるんだ。

なぜなら、

この2つの三角形は底辺BPを共有していて、

高さが同じだだからさ。

んで、もっといってやると、

△ABC=△DPC

になるんだ。

なぜなら、

• △ABC = △ABP + △PBC
• △DPC = △DBP + △PBC

でしかも、等積変形で、

△ABP = △DBP

ってわかってるからね。

だから、

△ABC = △PBC

になってるんだ。

等積変形についてもっと知りたいときは、

平行線と面積の記事をよんでみてね^^

Step5. 垂直二等分線をひく！

つぎは垂直二等分線をひいてみよう。

等積変形後でできた三角形の底辺で、垂直二等分線をかけばいいんだ。

えっ。

なぜ垂直二等分線をひくのかって？！

じつは、

三角形の底辺の中点を求めるのが目的なんだ^^

例題でいうと、

△PDCの底辺DCの中点を求めるってことだね。

さっそく、垂直二等分線をかいてみよう。

コンパスの脚を適当にひらいて、

左の点Dに針をおく。

そして、半円を、かく。

つぎは、右端っこにある点Cに針をおいて、

こっちでも半円をかいてみよう。

んで、2つの半円の交点をむすんでやると、

ほれ！垂直二等分線のできあがりさ。

ついでだから、

垂直二等分線と底辺の交点をMとしよう。

この点Mは、辺DCの中点だね。

もし、点Pと点Mを結んでやると、

△PDCの面積を二等分していることになるんだ。

なぜなら、

△PMCの面積は△DPCの半分になっていて、しかも、

△DPC = △ABC

だからね。

つまり、△PMCは△ABCの面積の半分でもあるってわけだ。

どう？？すっきりしたかな！？？！

まとめ：等積変形の三角形問題は垂直二等分線でクリア！

等積変形の三角形の問題！？

とりあえあず、コンパスと定規を準備。

そして、垂直二等分線をかいてやればいいのさ。

ガンガン等積変形していこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。