【中学数学】相似の証明問題の書き方がわかる3ステップ

相似の証明問題の書き方ってあるの？？

どうも、Drリードだよ。

中3数学の図形では、

図形と相似

を勉強してくよね。

この単元のなかでもやっかいなのが、

相似の証明問題

だ。

まず、証明とか苦手なのに、

図形の相似を証明しなきゃいけないときてる。

正直、きちいね。

でもね、じつは、

相似の証明問題には書き方のルールがあるんだ。

これならどんな相似の証明問題もイチコロさ。

相似の証明問題を書く前に準備する2つのこと

相似証明問題の書き方を紹介していく前に、

2つのことをやっておこう。

1. 図形に印をつけろ
2. 相似な三角形をさがす

つぎの相似の証明問題で練習してみようね。

つぎの2つの三角形が相似であることを証明しなさい。

 

 

ただし、

• AB = 5 cm
• BC = 6 cm
• DE = 10 cm
• EF = 12 cm
• 角B = 角E = 30°

とします。

Step1. 図に印を書き込む

まずは、

問題でわかってる条件（仮定）

を図にかきこんでみよう。

練習問題では、

• 三角形の辺の長さ
• 三角形の角度

がわかってたよね？？

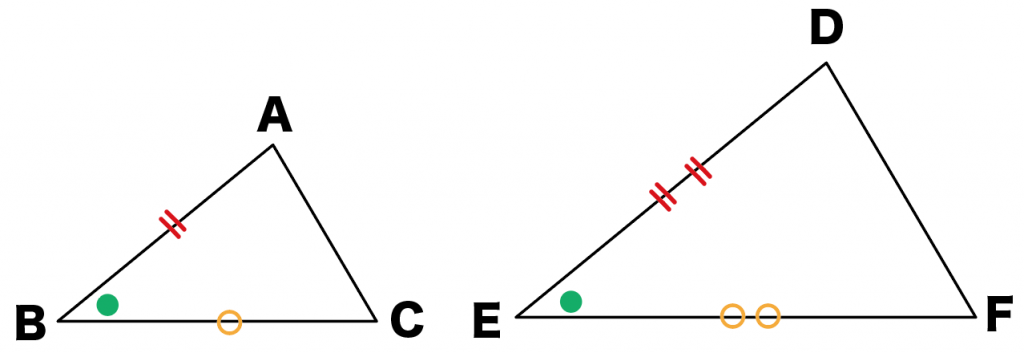
さっそく書き込んでやると、こうなる↓↓

んで、

同じ角度・辺の長さ同士に、「同じ印と色」をつけてやると、

こうなるね↓↓

Step2. 相似な三角形をさがす

つぎは、相似な三角形をさがそう。

三角形の相似条件にあてはまる2つの三角形をさがせばいいのさ。

念のため、三角形の相似条件を確認しておくと、

• 3組の辺の比がすべて等しい
• 2組の辺の比とその間の角がそれぞれ等しい
• 2組の角がそれぞれ等しい

だったよね？？

ってことで、練習問題をみてみると、

2組の辺の比とその間の角がそれぞれ等しい

がつかえそうってことに気づかない？？

だって、三角形の2組の辺の比が、

• AB : DE = 5:10 = 1 :2
• BC : EF  = 6 : 12 = 1 : 2

で両方1:2で等しいし、

その間にはさまってる角の、

• 角B
• 角E

が両方30°になってるからね。

えっ。簡単すぎるって？？！

本番の証明問題はもっと複雑でみつけにくいよ。

まだまだ油断大敵。

相似の証明問題の書き方がわかる3ステップ

それじゃあ、相似の証明を実際にかいてみよう。

書き方はつぎの3ステップ。

1. 図形を宣言
2. 自分でみつけた根拠をかく
3. 相似の条件と式をかく

Step1. 使う図形を宣言する

まずは、どの図形で相似を証明するのかを宣言しよう。

相似の証明問題では、おもに、

準備でみつけた「相似になりそうな三角形」を宣言することが多いね。

練習問題では、

△ABC と△DEFが相似疑惑だったよね？？

だから、証明のいちばん最初に、

△ABCと△DEFについて、

って宣言すればいいんだ。

Step2. 相似の根拠をかく

つぎは、

図形が相似になる根拠をかいていこう。

図や問題文からわかってることをかけばいいよ。

相似条件にあてはまる根拠をかいていけばいいのさ。

まずは、仮定からわかることを書いていこう。

問題文の中に書かれていることを数式にしてみよう。

練習問題では仮定として、

• AB : DE = 5:10 = 1 :2
• BC : EF  = 6 : 12 = 1 : 2
• 角B = 角E

がわかってたよね？？

この仮定だけで相似条件でつかえそうだから、

証明の根拠はこれだけでいいんだ。

Step3. 相似条件・式をかく

相似の証明の最後では、

なぜ、相似がいえるのか？？

という相似条件と、

宣言した図形が相似であること

を記号であらわしてみよう。

練習問題で言うと、

△ABCと△DEFが相似になってたね？？

つかった相似条件は、準備でもみてきたように、

2組の辺の比とその間の角がそれぞれ等しい

だ。

これにより、

△ABC ∽ △DEF

がいえるってかけばいい。

これで相似の証明はおわり！

実際に相似の証明をかいてみよう！

それじゃあ、この書き方で相似の証明をかいてみよう。

こんなかんじになるよ↓

まとめ：相似の証明問題の書き方は使いまくっておぼえろ！

最後にもう一度復習しておこう。

相似の証明問題を書く前の準備は、

• 図形に印をつける
• 相似な三角形をさがす

だったね。

んで、相似証明問題の書き方は、

• 図形を宣言
• 相似の根拠をかく
• 相似条件、相似の式をかく

の3ステップ。

これで何とか道は開けるよ。

何がわかっていて、あと何がわかれば、

相似の条件がそろうのか考えてみよう。

証明を書き始める前にしっかり用意してね。

次は「相似の証明問題でマスターしておきたい３つのパターン」について話す予定だよ。

Qikeru：学びを楽しくわかりやすく

 

1 Pocket

2016.09.27

相似の証明問題でマスターしておきたい3つのパターン

https://media.qikeru.me/similarity-proof-pattern

相似の証明ってどんな問題がでるの？？こんにちは、Drリードだよ。 相似でいちばんやっかいなのは、相似の証明の問題だね。これは文字通り、ある図形が相似であることを証明しなきゃいけない問題なんだ。テストによくでてくるから完ぺきにしておこう。 前回の記事では「相似の証明問題の書き方」を勉強してきたよね？？今日は、もう一歩踏み込んで、相似の証明問題でよくでてくる3つのパターンを勉強していくよ。テスト前に参考にしてみて。  相似の証明問題でよくでてくる3つのパターン相似の証明には基本の３パ...

相似の証明を極めたいやつは読んでみてくれ。

それじゃあ

Drリード

DR. リード

公立中学校理科数学講師、進学塾数学講師、自宅塾 高校数学英語化学生物指導、国立大学医学部技官という経歴を持つスーパー講師。よろしくな！