相似の証明ってどんな問題がでるの??
こんにちは、Drリードだよ。
相似でいちばんやっかいなのは、
相似の証明の問題
だね。
これは文字通り、
ある図形が相似であること
を証明しなきゃいけない問題なんだ。
テストによくでてくるから完ぺきにしておこう。
前回の記事では「相似の証明問題の書き方」を勉強してきたよね??
今日は、もう一歩踏み込んで、
相似の証明問題でよくでてくる3つのパターン
を勉強していくよ。
テスト前に参考にしてみて。
相似の証明問題でよくでてくる3つのパターン
相似の証明には基本の3パターンがあるよ。
それぞれの特徴と証明の進め方を確認していこう。
図形を見て、
「あっ,○○○タイプだっ」
てわかるようになれば一安心だね。
問題パターン1. 「リボン型の図形」
1つめによくでてくる証明問題のパターンは、
リボン型の図形
だ。
この問題の図形は、文字通り、
リボンの形
をしているよ。

たとえば、つぎのような問題だね。
証明問題1.
つぎの△AODと△COBが相似であることを証明しなさい。
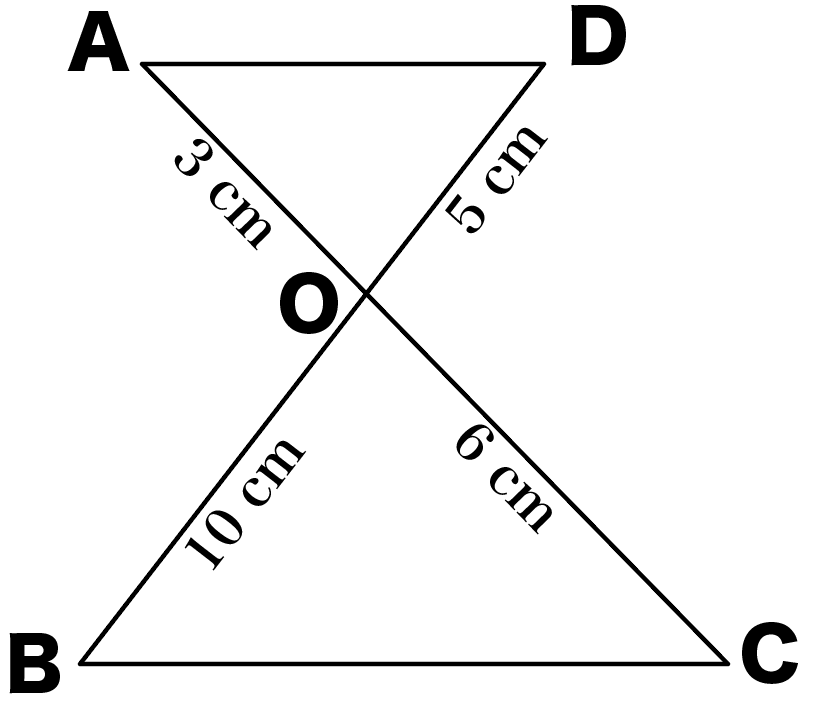
この問題の場合、2つの辺の長さがわかっているね。
あとはどの相似条件にあてはまるかだ。
2つの辺がわかっているから、つぎの相似条件のどっちかにあてはまるはずだね。
- 3組の辺の比がそれぞれ等しい
- 2組の辺の比とその間の角がそれぞれ等しい
1つめの相似条件にあてはまるためには、
ADとBCの長さ
が必要になってきちゃうね。
これはたぶん、おそらく、無理!
超能力ならいけそうだけどね。
ってことで、2つめの相似条件の、
2組の辺の比とその間の角がそれぞれ等しい
が使えそうだ。
これなら、長さがわかってる2つの辺にはさまれた、
- 角AOD
- 角COB
の大きさが等しいってわかるからね。
だって、対頂角だから等しいんだもん。
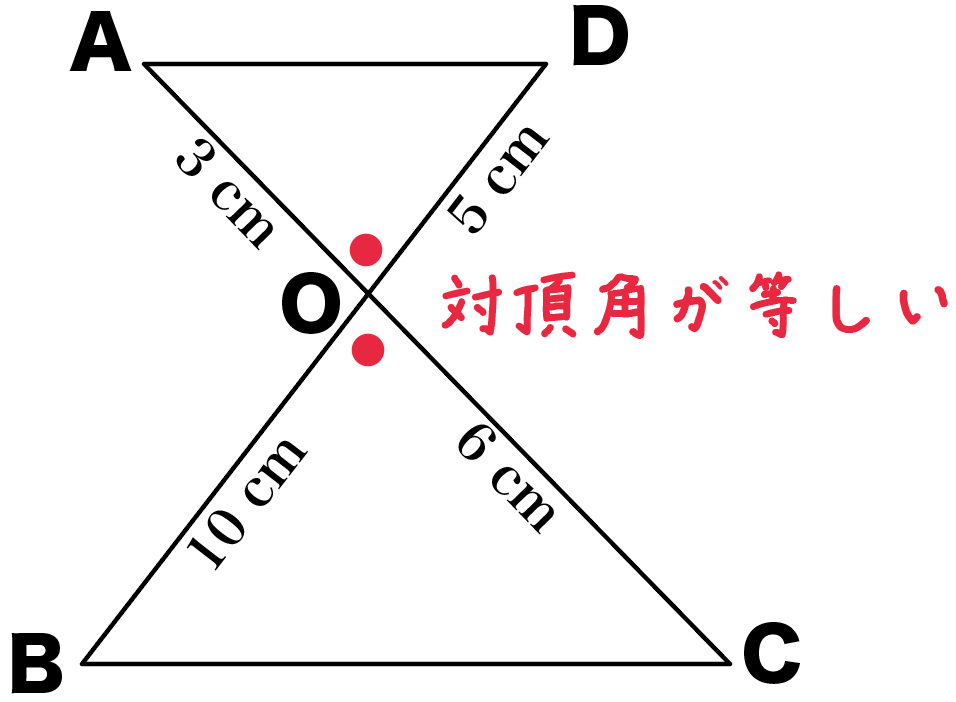
ってことで、
- AO : CO = 3 : 6 = 1 : 2
- DO : BO = 5 : 10 = 1 : 2
- 角AOD = 角COB
になるから、相似条件の、
2組の辺の比とその間の角がそれぞれ等しい
がつかえそう。
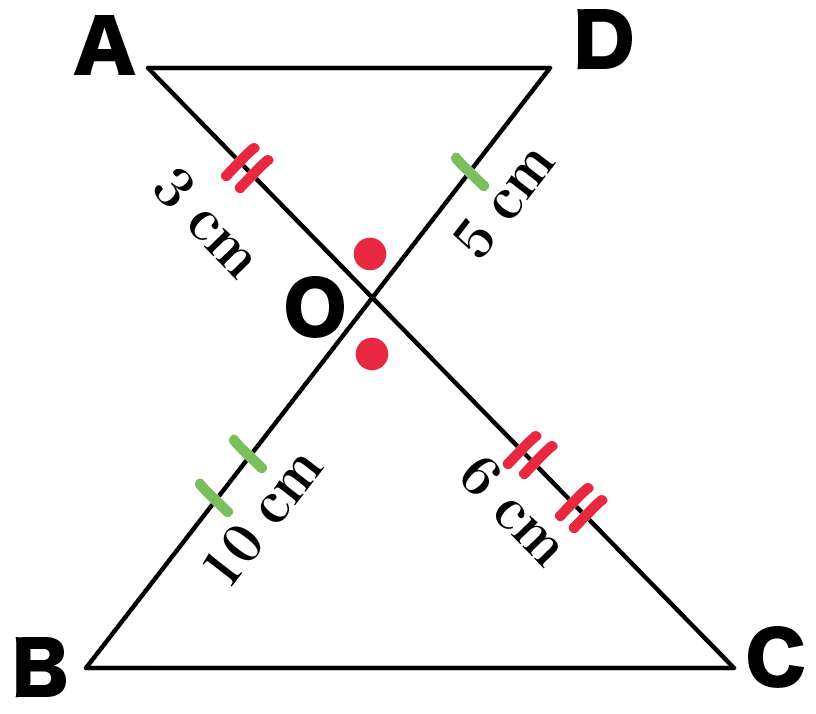
以上をふまえて、相似の証明の書き方通りにかいてやると、
仮定から、
AO:CO = 3 : 6 = 1 : 2 ・・・①
DO:BO = 5 : 10 = 1:2 ・・・ ②
対頂角は等しいので、
∠AOD = ∠COB・・・ ③
①②③より、
2組の辺の比とその間の角がそれぞれ等しいので、
△AOD ∽ △COD
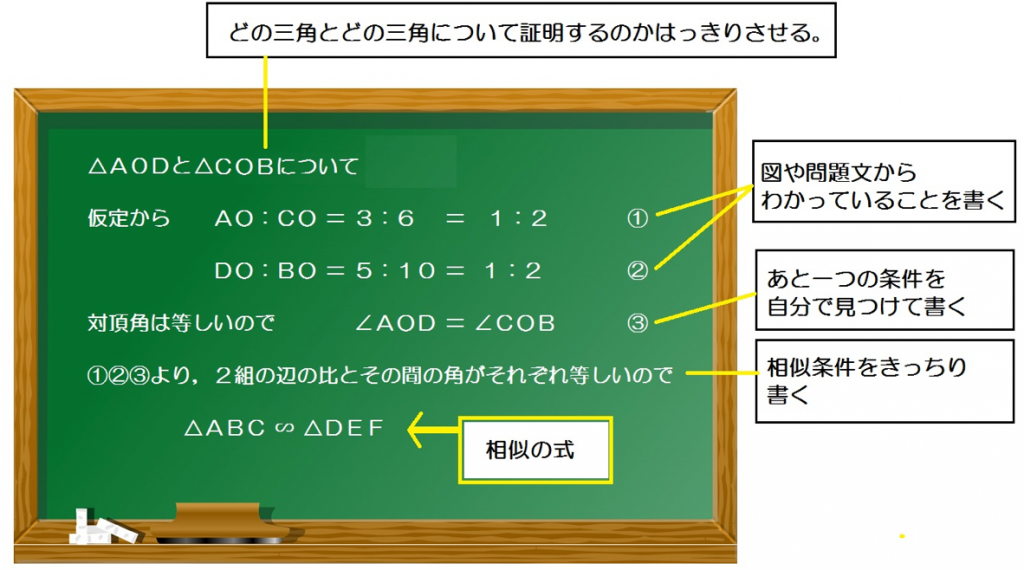
になるね。
パターン2. 「ひねくれ回転型」
つぎの相似証明問題のパターンは、
ひねくれ回転型
だ。

これは文字通り、
図形が回転していて、相似がみえにくくなってる問題ね。
たとえば、相似なイラスト同士だったら回転していても、
どことどこが対応するかわかりやすいよね。
特徴があるんだもん。

でも図形だと、そうはいかない。
向きが変わるだけでわからなくなっちゃうんだ。
たとえば、つぎのような証明問題。
証明問題2.
つぎの図形のなかから相似な図形をさがして、
その相似を証明しなさい。
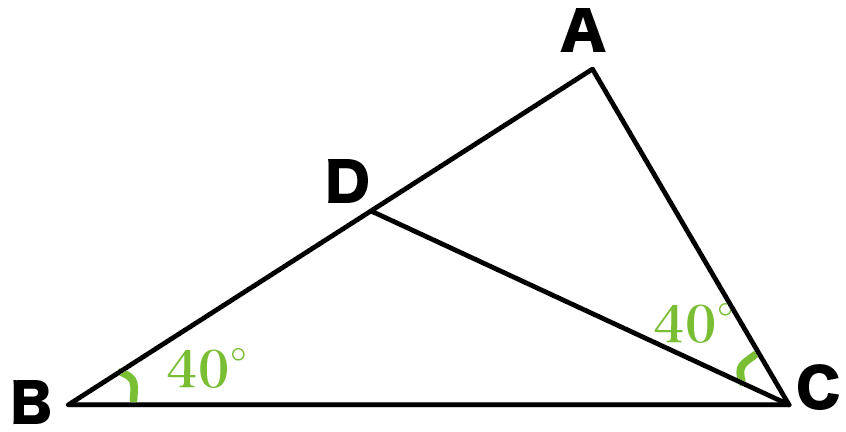
このタイプの証明問題では、
面倒でも別々に切り離して、
対応する辺や角度を確認してみるといいよ。
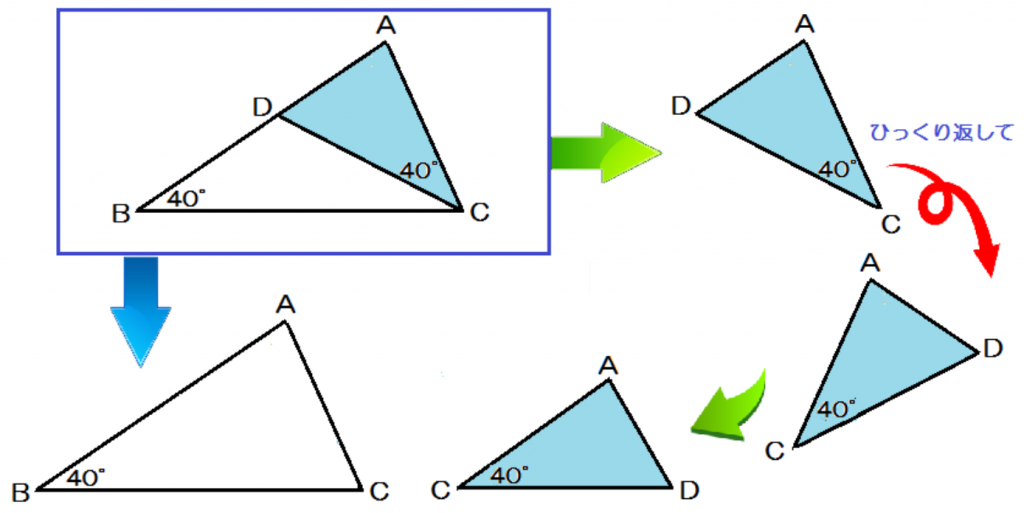
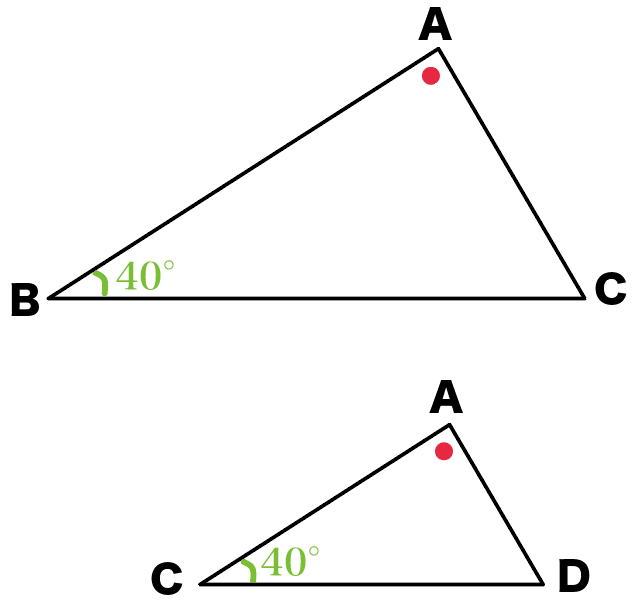
すると、
△ABCと△ACDが相似ってことがわかるね。
なぜなら、
- 角ABC = 角ACD
- 角BAC = 角CAD
になって、2組の角がそれぞれ等しいっていう相似条件がつかえるからね。
えっ。図形を回転させるのがむずかしいって!??
そんなときは、
対応する辺や角を大きさ順に、
「大中小」とか「長中短」とか
っていう順序をつけるといいよ。
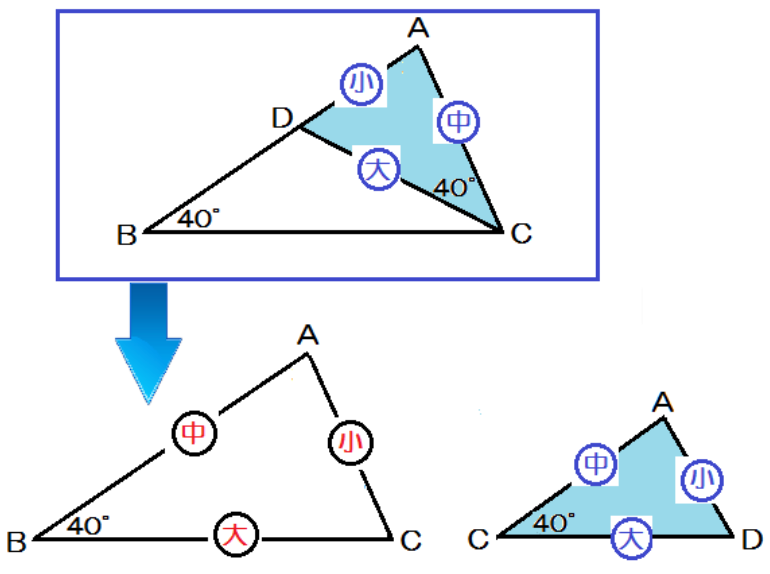
こんなかんじで、ひねくれて回転している図形をなんとかして、
対応する辺の順番にそろうように回転させてみてね。

実際に証明をかいてみると、こんな感じになるよ↓↓
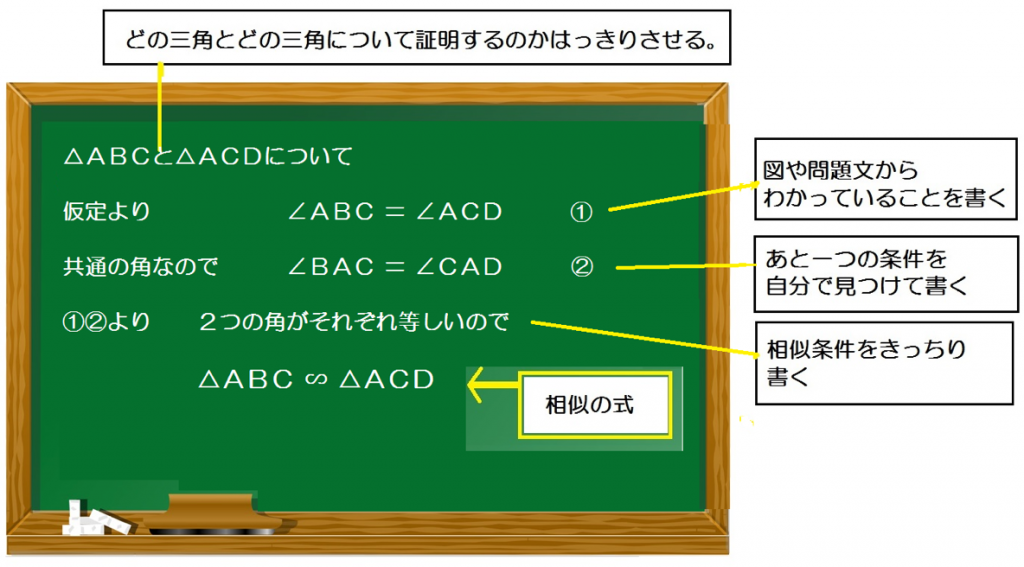
△ABCと△ACDについて
仮定より
∠ABC = ∠ACD ・・・ ①
共通の角なので、
∠BAC = ∠CAD・・・②
①・②より、
2つの角がそれぞれ等しいので、
△ABC ∽ △ACD
パターン3. 直角三角形から垂線
最後の相似の証明のパターンは、
直角三角形で垂線がおろされてる問題
だ。

たとえば、つぎの相似の証明問題だね。
証明問題3.
つぎの図形のなかから相似な図形をさがして、
相似であることを証明しなさい。
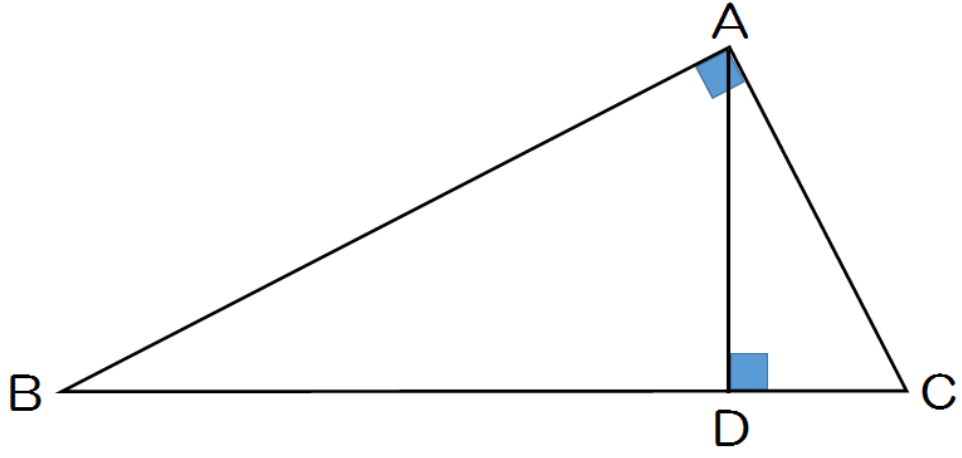
このさっきの相似の証明問題とおなじ。
対応する辺・角が重なるように回転させればいいんだ。
わかりやすいように、△ABDを△ABCの外にとりだして回転させてみると、
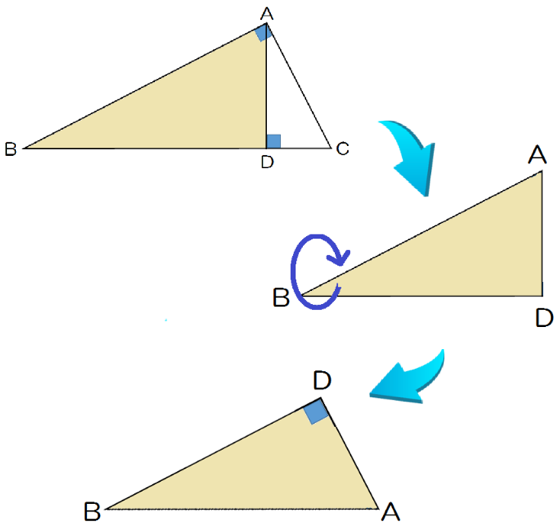
あら!
△ABCと△DBAが相似っぽい!
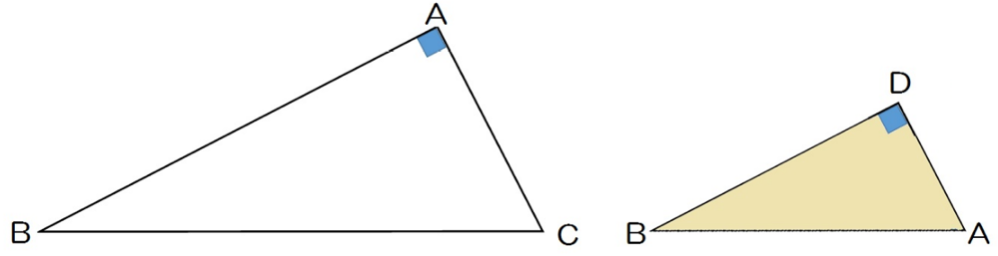
なぜなら、
- 角BAC = 角BDA = 90°
- 角ABC = 角DBA (共通)
だからね。
2組の角がそれぞれ等しい
っていう相似条件が使えることになるんだ。
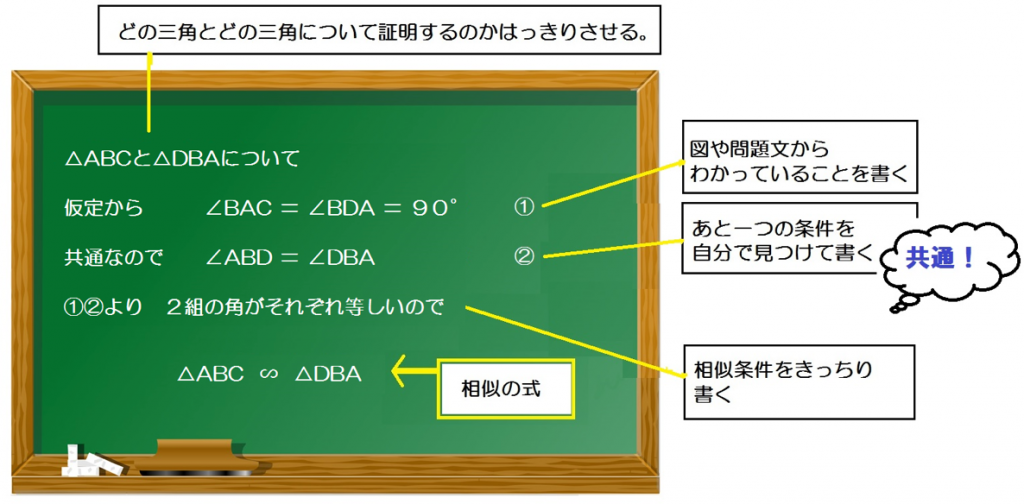
この証明をちゃんとかいてやると、こうなるよ↓↓
△ABCと△DBAについて
仮定から、
∠BAC = ∠BDA = 90°・・・①
共通なので、
∠ABD = ∠DBA・・・②
①②より、
2組の角がそれぞれ等しいので
△ABC ∽ △DBA
まとめ:相似の証明問題の基本は3パータン!
相似の証明問題はめんどくさそうにみえるけど、じつは、
どの問題もよく似ていて、
パターンがみえるんだ。
なれるまでたくさん相似の証明問題をといてみよう。
それじゃあ!
Drリード

公立中学校理科数学講師、進学塾数学講師、自宅塾 高校数学英語化学生物指導、国立大学医学部技官という経歴を持つスーパー講師。よろしくな!






「証明問題3.」ですが、もう一つの三角形「△ACD」も相似になりますよね?
△ABCと△ACDについて
仮定から、
∠BAC = ∠CDA = 90°・・・①
共通なので、
∠ACB = ∠ACD・・・②
①②より、
2組の角がそれぞれ等しいので
△ABC ∽ △ACD
>「証明問題3.」ですが、もう一つの三角形「△ACD」も相似になりますよね?
△ABCと△ACDについて
仮定から、
∠BAC = ∠CDA = 90°・・・①
共通なので、
∠ACB = ∠ACD・・・②
①②より、
2組の角がそれぞれ等しいので
△ABC ∽ △ACD
そうだね!!
たとえば、?:?:?:?:?:?、になることを証明しなさいとかの問題はどうやってとくのですか?
>たとえば、?:?:?:?:?:?、になることを証明しなさいとかの問題はどうやってとくのですか?
まずは2つの図形の相似を証明するよ。
相似を証明できたら、相似な図形同士の対応する辺の比が等しいことを使おう
線分ABと線分CDがあり、AB//CDである。
点Aと点D、点Bと点Cをそれぞれ結び、その交点をEとする。
AE=3cm、CE=5cm、DE=4cmのとき、BEの長さを求めなさい。
>線分ABと線分CDがあり、AB//CDである。
点Aと点D、点Bと点Cをそれぞれ結び、その交点をEとする。
AE=3cm、CE=5cm、DE=4cmのとき、BEの長さを求めなさい
これはリボン型の相似な図形だね。
AE:EDを計算して、それを使ってCEの長さからBEを求めてみよう
もっと簡単な方法は,無いですか?
分かりやすかったです