放物線の頂点と軸ってどこのなの??
ある日、数学が苦手なかなちゃんは、
放物線に出会いました。

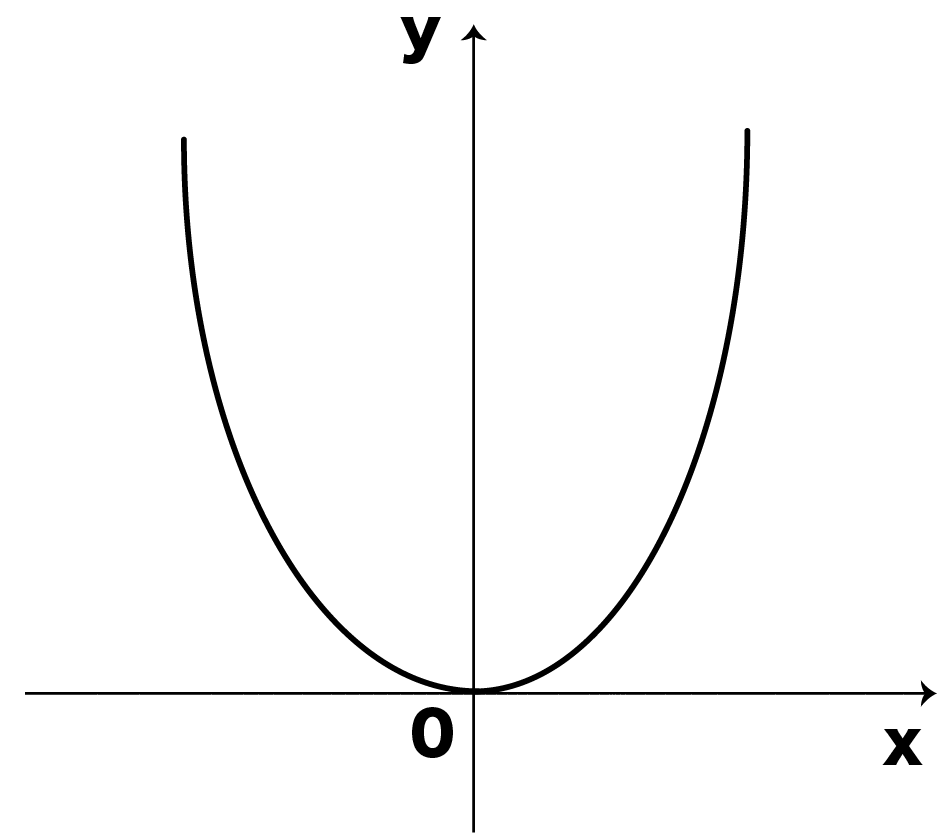
二次関数y=ax2のグラフ。。。
放物線わけわかんない泣
ゆうき先生だ!
いろいろな名前
があるの知ってたかな??
- 放物線の軸
- 放物線の頂点
とか。
ちょうてん・・・・
じく・・・・・
漢字で覚えたほうがいいよ。
でも、聞き慣れない言葉だと、どうしても・・・・・・
じゃあ、『軸』はどう?
y軸とかx軸の仲間??
今まで、グラフで見てきたよね!
『頂点』は初めましてかな?
『頂点』って、どんな点だろう??
放物線の軸ってなに??
放物線の軸からみていこう。
放物線の対称軸のこと
なんだよ。
そのときの折り目を「対称軸」というの。

y軸
になってるね。

じゃあ、放物線の頂点とはなに??
つぎは放物線の「頂点」。
放物線の頂点とは、
「放物線の軸」と「放物線」の交点のこと
をいうんだ。

よくわからんねーー
二次関数y=ax2だったら、
原点の(0, 0)
が頂点だね。

よくわからないときは、
山の頂上をイメージして。

「山の頂点みたいに盛り上がってるところ」が頂点
っておぼえればいいの。
y = ax2で「aが0より小さいとき」は、
ほんとうの山みたいになるよ。

二次関数y = ax2の放物線の軸・頂点はいつも・・・?
「y=ax^2」の放物線
をくわしくみていこうか。
この放物線には、
頂点と軸がいつだって同じ!
っていう特徴があるんだ。
いつも頂点が(0,0)で、
軸はy軸ってこと??
いろいろなグラフをイメージするといいよ。
たとえば、
比例定数aが正と負のときを考えてみよう。
こんなかんじで、
上下逆さまになるじゃん?

頂点も軸も一緒だ!
じゃあ、比例定数aを大きくしたり、
小さくしたりしてみてよ。
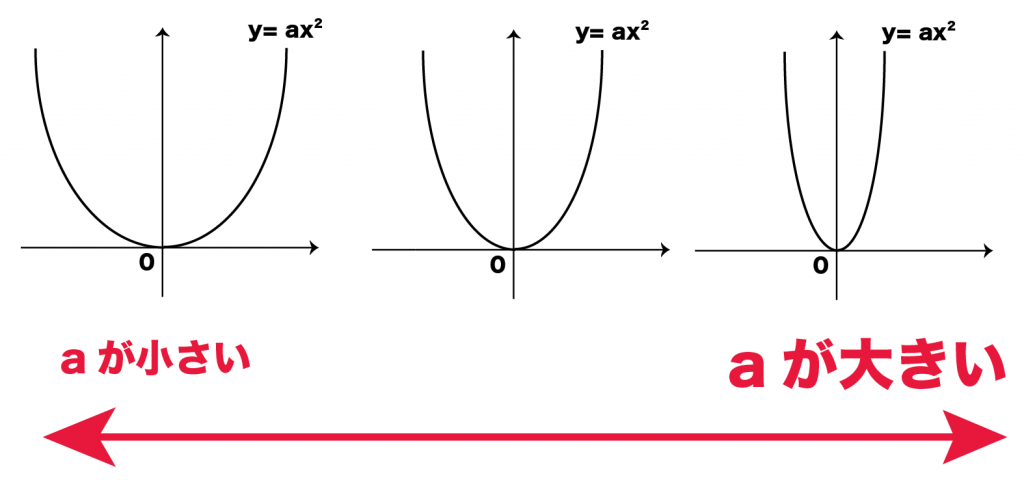
頂点と軸はいっしょだ!
そう!
二次関数y=ax2の頂点と軸はいつも同じなんだ。
放物線の軸と頂点は高校数学ではどうなる??
頂点と軸に興味を持ってくれたから、
細かいこと話したいけど、
どう?
高校数学にどうつながってるんだろう・・・・・
高校でも変わらないよ♪
……
(納得いかない)
まだあるから!
高校に入ると、
色んなところに頂点や軸がある二次関数
が出てくる。
ちなみに、この二次関数の頂点と軸はわかるかな?

えっと、
頂点が(1,1)で、
軸がx=1
ってこと?

そう!
それが分かれば十分!
興味があって、高校まで待てないなら、
詳しく調べてね♪

年齢不詳の先生。教育大学を卒業してボランティアで教えることがしばしば。




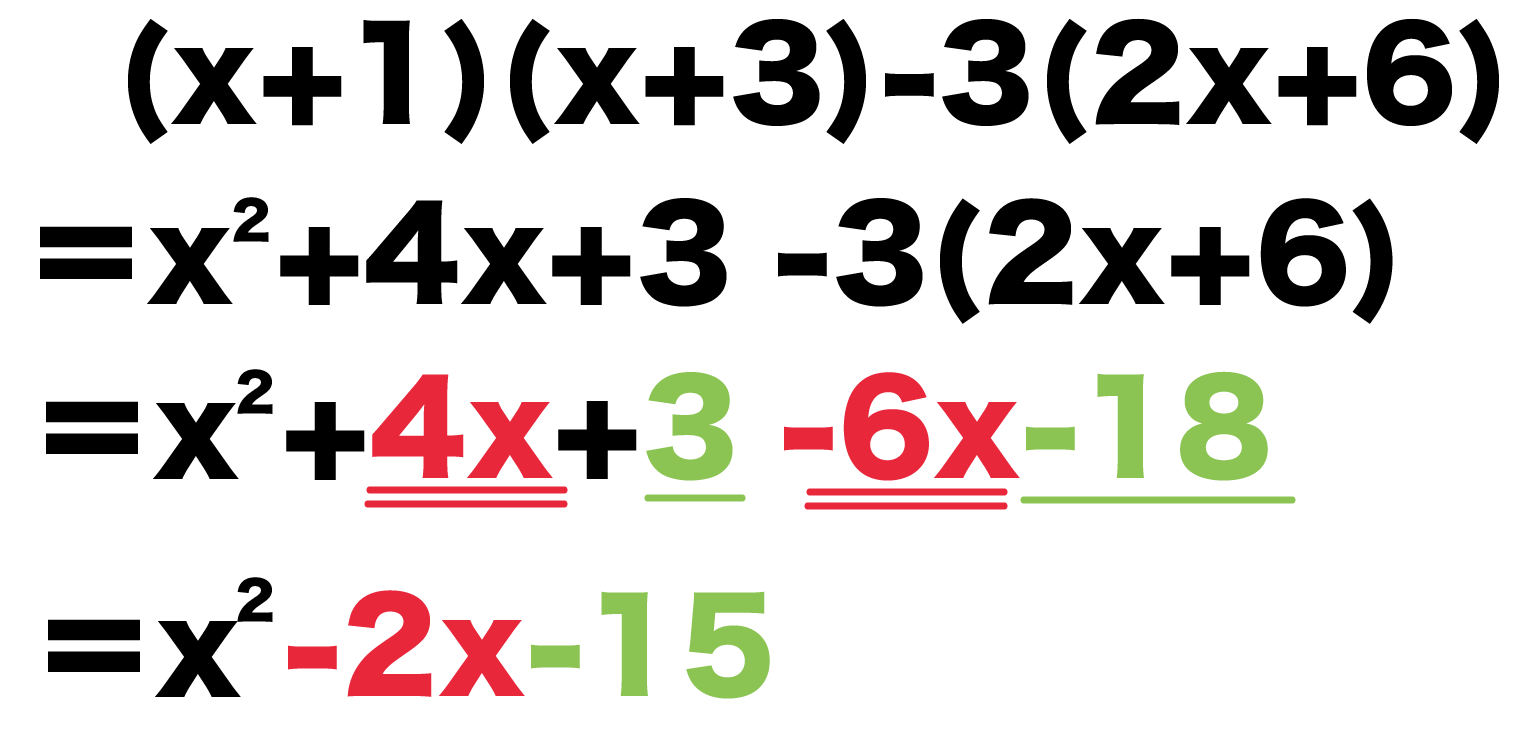
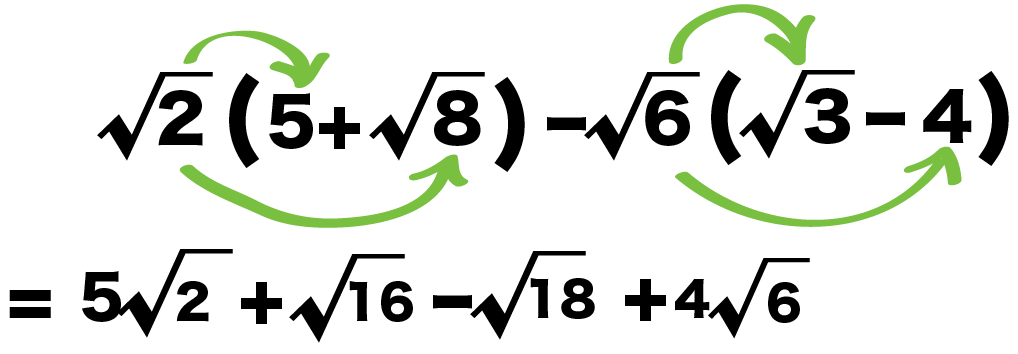



放物線が横向きの場合はどうしたらいいのでしょうか?