正方形と扇形の面積をつかった問題??
こんにちは!この記事をかいているKenだよ。ガムはかむほどうまいね。
「正方形」と「扇形」の面積をつかった問題。
たまーにでてくるよね。
たとえば、つぎのような問題だ。
例題
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。

えっ。なんか虫みたい!?
えっ、キモ・・・・
って避けたくなる気持ちもわかる。難しそうだし。。
だけど、解き方をしっていれば、つぎの3ステップで計算できちゃうんだ。
- 扇形の面積を計算する
- 正方形の面積を計算する
- 扇形の面積の和から正方形をひく
正方形と扇形の面積をつかった問題がわかる3ステップ
例題をといてみよう。
例題
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。

Step1. 扇形の面積を計算する!
まず、扇形の面積を計算していくよ。
えっ。
扇形なんてどこにもないって!??
たしかにね。
だけど、よーくみてみて。

じつはこの図形のなかには、
- 扇形ABD
- 扇形BCD
の2つの扇形がかくれているんだ。
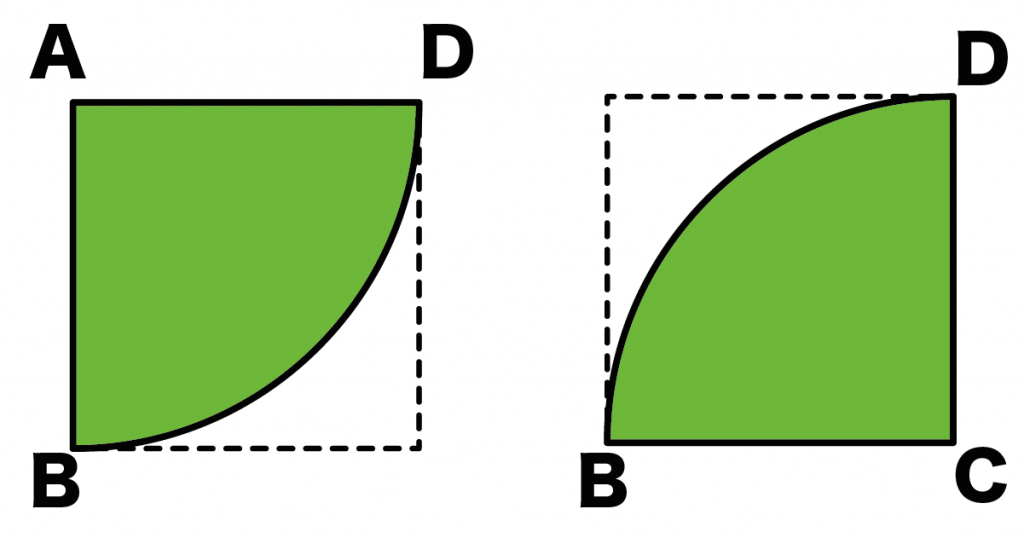
それぞれ同じ面積になっているね。
計算してやると、
扇形ABD = 扇形BCD
=半径×半径×中心角÷360
= 8 × 8 × 90°÷360
= 16 [cm²]
になる!
Step2. 正方形の面積を計算する!
つぎは、正方形の面積を計算していくよ。
例題でいうと、正方形ABCDだね。
(正方形の辺の長さ)×(正方形の辺の長さ)
だったね?
ってことは、正方形ABCDの面積は、
8× 8
= 64[cm²]
になるんだ!
Step3. 「扇形の面積」をたして「正方形の面積」をひく!
いよいよ最後の仕上げ。
「扇形の面積」をたして「正方形の面積」をひいてみよう。
例題でいうと、
- 扇形ABD
- 扇形BCD
をたして、正方形ABCDの面積をひけばいいんだ。
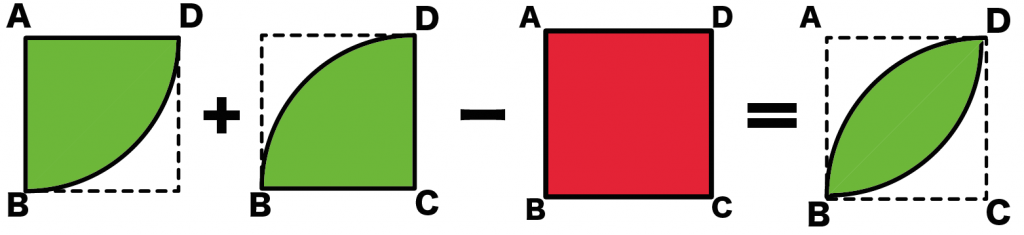
だから、
(扇形ABD)+(扇形BCD)-(正方形の面積)
= 16π + 16π – 64
= 32π – 64 [cm²]
になるね。
どう??計算できたかな??
まとめ:扇形の面積をたして正方形の面積をひこう!
「扇形の面積」をたして、
「正方形の面積」をひけばいいんだ。
いろいろな問題にチャレンジしてみてね^^
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





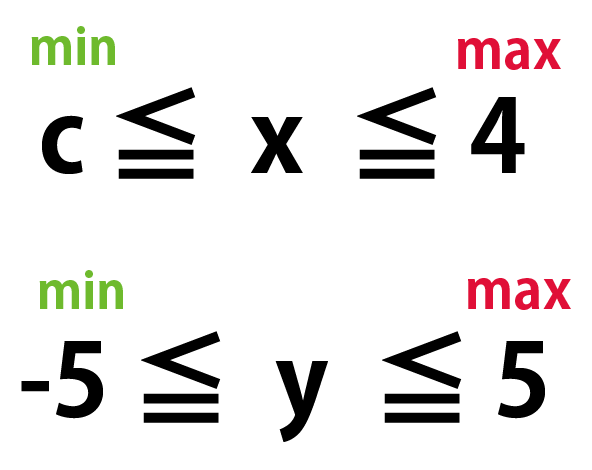


AB=8㎝、BC=12㎝の長方形ABCDがあります。辺AB上に点P、辺AD上に点Qをとり、線分DQの長さが線分APの長さの2倍になるようにします。△PBCと△DQCの面積の和が51㎠になるとき、APの長さは何㎝になりますか。APの長さをx㎝として方程式を作り、求めなさい。
xを使って、
△PBCの面積 + △DQCの面積 = 51㎠
という方程式を作ってみよう!
勉学を20年離れた者です。再度専門学校へ行くための入試がマジかに控えております。
過去問を買いましたが、回答がありません。勉強の為、このサイトを有難く使用させて頂いております。解けない問題があり、教えて頂きたくメールをしました。回答してもらえれば、有難いです。
質問1
一辺の長さaの正方形ABCDの内側に点Pがある。∠APBが鋭角(90°より小さい角)になるような点Pが存在する部分の面積aで表せ。円周率はπとする。
質問2
正三角形ABCの各頂点から対辺に引いた垂直は、1点Oで交わる。
OA=aとおくとき、次に答えよ。
(1) 正三角形ABC1辺の長さをaで現せ。
(2)正三角形ABCの面積をaで現せ。
以上です。 よろしくお願い致します。
>質問1
一辺の長さaの正方形ABCDの内側に点Pがある。∠APBが鋭角(90°より小さい角)になるような点Pが存在する部分の面積aで表せ。円周率はπとする。
角APBがちょうど90度になる点を探しましょう。そこを境にAPBが鋭角か鈍角なのかがわかれるはずです
>質問2
正三角形ABCの各頂点から対辺に引いた垂直は、1点Oで交わる。
OA=aとおくとき、次に答えよ。
(1) 正三角形ABC1辺の長さをaで現せ。
(2)正三角形ABCの面積をaで現せ。
BからACに引いた垂線とACとの交点をHとしましょう。
△AOHで頂角30度の直角三角形の比を使ってAHの長さをaで表しましょう。
今度は△ABHでACの長さを使って、角度60度の直角三角形の比を使ってABの長さをaで表しましょう。
1辺の長さがわかればあとは高さBHもaで表していつも通り三角形の面積の公式で計算すればいいですね
底面の半径が、6cm、母線の長さが10cm、の側面となるおうぎ形の中心角を求めなさい。という問題がわかりません
おしえてください!!あと、三角錐の定義とかの定義の意味がよくわかりません。おしえてください!!
>底面の半径が、6cm、母線の長さが10cm、の側面となるおうぎ形の中心角を求めなさい。という問題がわかりません
扇型の中心角の求め方を読んでみて!
>あと、三角錐の定義とかの定義の意味がよくわかりません。おしえてください!!
定義は意味ってことかな!
三角錐は底面が三角形の錐体(先っちょがとんがってるやつ笑)だ
それで、答えはどーなるのですか?
半円に直径2cmと直径4cmの半円があります。その周の長さと面積の求め方を教えてください
こんなのは?正方形の中に扇形があって扇形の中に半径が2つ入ってて半径が重なってるとこ以外の面積を求める求めるの
一辺が5cmの面積はどうなるのですか?