円周率の意味とはなんだろう!?よくわかんね。
こんにちは、この記事をかいているKenだよ。メガネ探知機がほしいね。
今日から「円とおうぎ形」を勉強していくよ。この単元でいちばん出現するのは、
そう、
円
だ。
円。まるっこい奴のことさ。
教科書によると、
中心Oと円周上の点を結ぶ線分の長さは、円周上の点をどこにとっても等しく、この円の半径になります。
って書いてあるね。
つまり、ただ丸っぽいだけじゃなくて、中心から等しい距離に線をかきまくってできる図形のことなんだ。
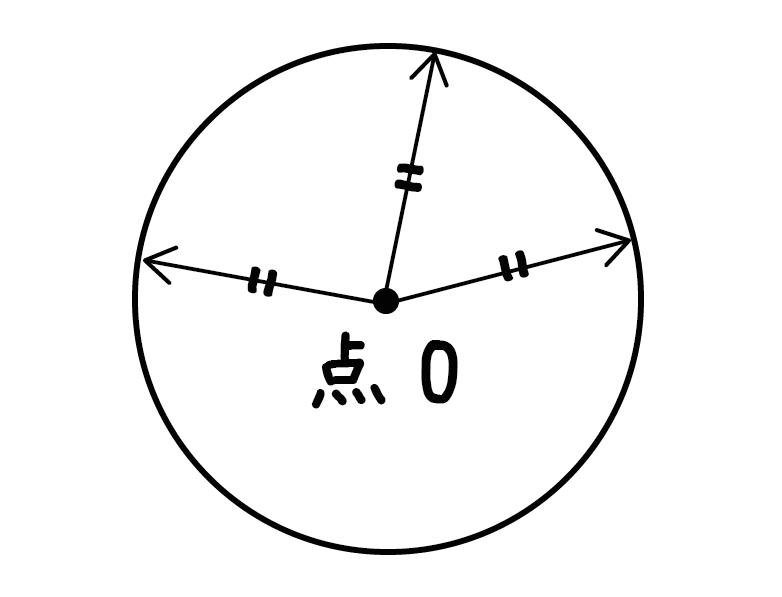
これが「円」だ。
この円について勉強していく上で、知っておくべき用語の1つに、
円周率
っていうものがある。これがむちゃくちゃ重要。円周率を知らないとテストで一問も解けないままゲームセットになっちまうんだ。

それじゃあ、円周率の意味とはなんだろう!??
円周率とは○○の意味がある。
教科書で「円周率の意味」を確認してみよう。中1数学の教科書には、
円周の直径に対する割合です
って説明があるね。円周の直径に対する割合?? えっと・・・ちょっと意味がよくわからないよね。うん、堅苦しい。
もっとわかりやすくいうと、円周率とは、
円周(円のまわりの長さ)が直径の何倍になっているか
ということを表した数字なんだ。小学校のとき、円周率は約3.14って習ったでしょ?? つまり、
円周は直径のだいたい3倍の長さになっているよ^^
ってことなんだ。
たとえば、直径1cmの円があったとしよう。
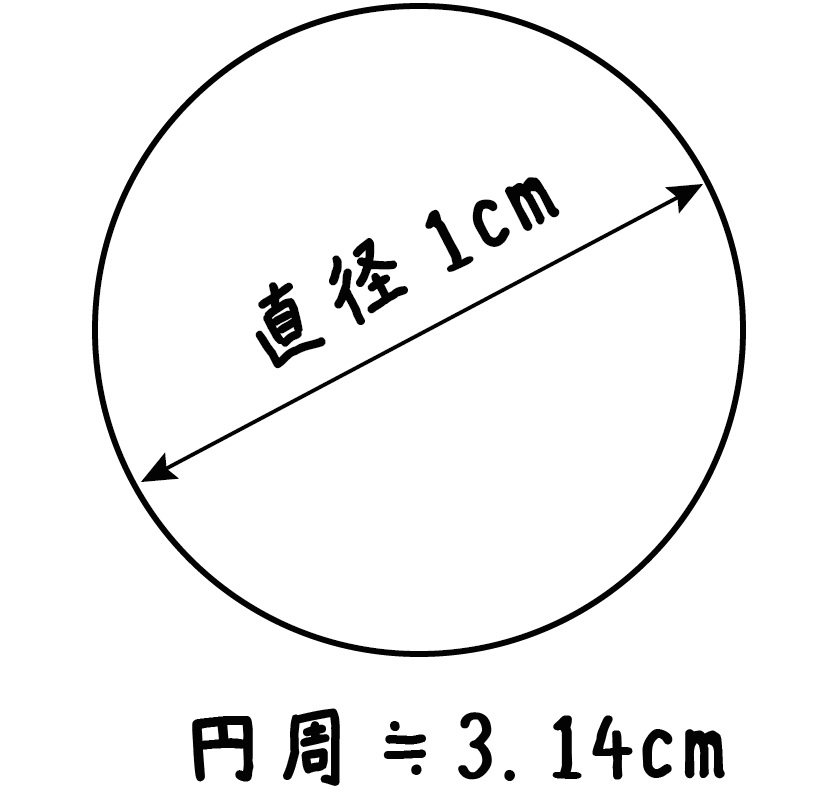
この円周の長さはだいたい3.14cmってことになるわけ。
じつは、この円周率っていうのはむちゃくちゃすごいことなんだ。
なぜかっていうと、
円の大きさを変えても円周率は変わらないからね。たとえば、「小さい円」でも「大きい円」でも決まって、直径の3.14倍が円周の長さになっているんだ。
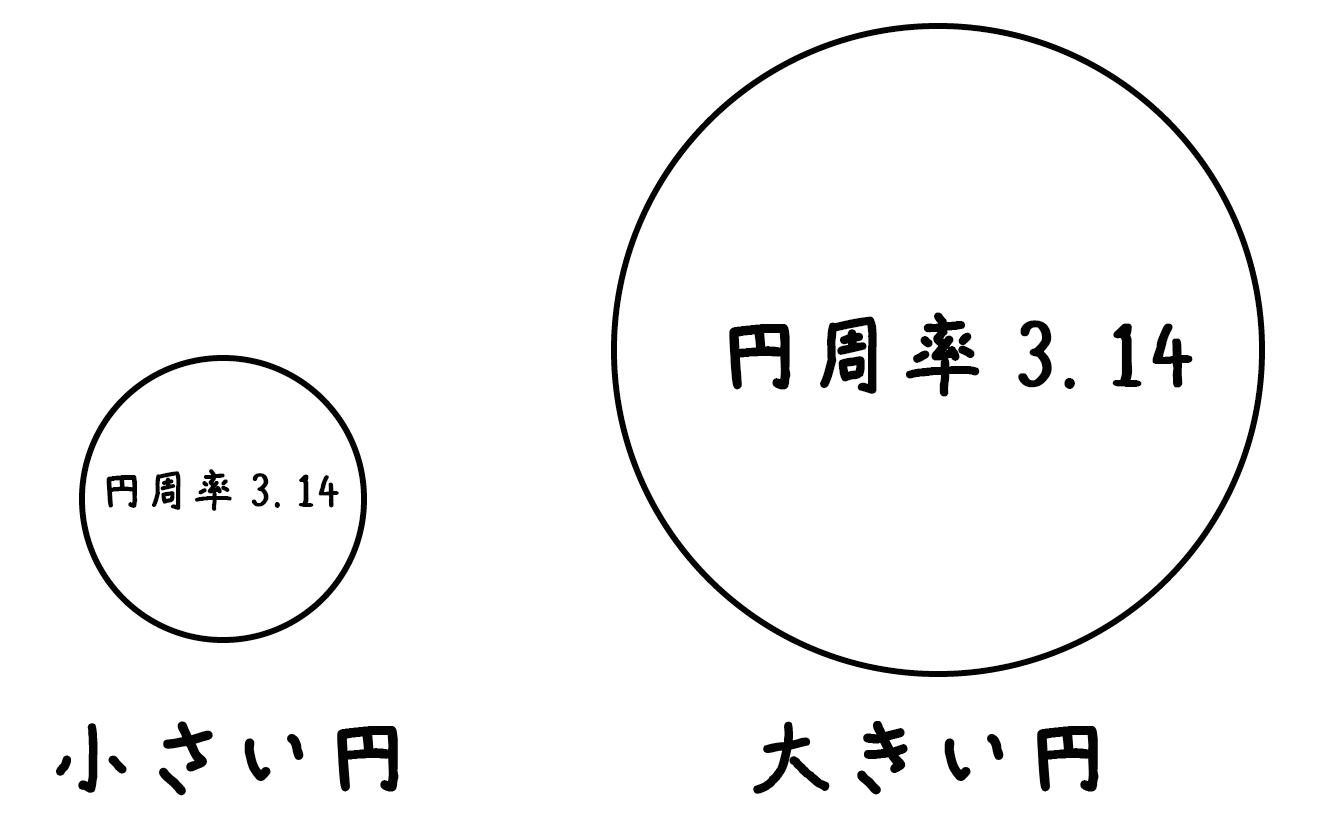
どんなに大きさを変えても「直径」と「円周の長さ」の関係が変わらない。
これってスゴイよね?? もはや地球の神秘のひとつといってもいいぐらいさ。
中学数学では円周率を「π(パイ)」とする
小学校の算数では、
円周率は3.14である
って教わってきたよね。
だけれども、超厳密にいってしまえば、円周率は3.14じゃあない。
円周率は無限につづく終わりがない数字(無理数)なんだ。
3.14のつづきをちょっと書いてみると、
3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502….
こんな感じで無限につづいていくんだ。
マジ、終わりがない。
円周率って3.14に近い数字だけれども、3.14ではないんだ。でも、いちいち円周率を長く書いていたらテスト用紙がいくらあっても足りない笑
そこで中学数学では、
ギリシャ文字のπ(パイ)
を円周率としてあげることにしたんだ。パイって食べるお菓子のことでもないし、ドラゴンボールにでてくるタオパイパイでもない。
したがって、
円周の長さは直径のπ(パイ)倍である
ってことが言えるね^^
まとめ:円周率は「円周と直径の比」である
円周率の意味についてちょっとスッキリしたかな??
次回はいよいよ円の面積・円周の長さの求め方についてみていこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。









1πとπは同じものですか?
同じものですね!
整数+πは可能ですか?
例えば、8π+3=11πとなるのですか?
ならないね!
8π + 3πなら11πになるけどね
πは=3.14ってことですか?
>πは=3.14ってことですか?
イコールではないかな。
π≒3.14
本当は4以降も円周率は続くからね
円周率とは、何か
直径と円周の比のことだよ。
円周が直径の何倍になっているかを表していて、だいたい3倍ぐらいになってるわけ。どんな大きさの円でもね
円周率はなぜ3.14…なんですか?
>円周率はなぜ3.14…なんですか?
自然の神秘さ。神の領域だよ
πは文字扱いですか?数字扱いですか?
例えばπxという式があったとしてこれは1次式ですか?2次式ですか?
Πは文字扱いでいいよ。
ってことで、πxは一次式
中1の問題なのですが直径がXセンチの円の周の長さをyセンチとする。この時yをXの式で表すとy=πXになるみたいなんですけどこれは周の長さ=円周率(約3.14)✖️Xということでいいんですか?
>中1の問題なのですが直径がXセンチの円の周の長さをyセンチとする。この時yをXの式で表すとy=πXになるみたいなんですけどこれは周の長さ=円周率(約3.14)✖️Xということでいいんですか?
そうだね!
3xなどにπを付け加えるとするとXの後に付けますか?それとも3とXの間ですか?
>3xなどにπを付け加えるとするとXの後に付けますか?それとも3とXの間ですか?
πは数字よりもあと、文字よりも前におこう。
ってことで、3πxだ。使って行くうちになれるよー
π+πは?
>π+πは?
文字式の計算と同じだよ。
a+aと同様に計算してみよう
π-πをするとπは消えるの?
(例)80πcm²-50πcm²=30?or30π??
>π-πをするとπは消えるの?
(例)80πcm²-50πcm²=30?or30π??
例の場合、πは消えないよ!30πが正解だ。
πは他の文字のaとかxとかyとかと使い方は同じだね!
おうぎ形の弧の長さ=底面の円周の解き方はいったいどうすれば…
>おうぎ形の弧の長さ=底面の円周の解き方円錐の表面積の求め方を読んでみて!
質問① π=3.14…ですよね?
質問② ってことは、円の面積を求める式は、“半径×半径×π”ってことですか?
>質問① π=3.14…ですよね?
質問② ってことは、円の面積を求める式は、“半径×半径×π”ってことですか?
その通り!
分数 有りの 計算を教えて下さい。
>分数 有りの 計算を教えて下さい。
通分するといいよ!分母を共通のものに揃えるのさ
πは何年生で習うの?
>πは何年生で習うの?
中1かな!
πは具体的にどう言うことですか?
>πは具体的にどう言うことですか?
直径と円周の長さの比だね
πという答えを1πと書いたんですが、○になりますか?
>πという答えを1πと書いたんですが、○になりますか?
う〜ん、△かな〜
πは文字式と同じで1がかかってる時は省略できるね!
入試なんですけど
○か×ならどっちですか?
うーん、その人次第だろうなあ
400-100πの場合はどうなるんですか。
>400-100πの場合はどうなるんですか。
それ以上計算できないからそのままでいいよ〜
地球の円周に1mの縄を追加したら幅はどの程度広がるか?
・・・現在72歳になるが、中校生の頃得意になって計算したら“人間が腰を曲げて通過可能”と答えが出た記憶があります。最近小中学生となった孫等に質問しても私が計算式を忘れたので、恐縮ですが地球を原点として「外周が1m長くなった時」の比較する計算式をご教授願います
>地球の円周に1mの縄を追加したら幅はどの程度広がるか?
・・・現在72歳になるが、中校生の頃得意になって計算したら“人間が腰を曲げて通過可能”と答えが出た記憶があります。最近小中学生となった孫等に質問しても私が計算式を忘れたので、恐縮ですが地球を原点として「外周が1m長くなった時」の比較する計算式をご教授願います
まずは地球の円周の長さを計算してみましょう。直径x円周率ですね。
次は1m足した長さを計算。
最後に、長くした後の直径をdとして
d × 円周率 = 長くした後の地球の円周の長さ
というdの方程式を作り、dについてとけば幅がどの程度広がったのかわかると思います!
π=3.14・・・・・と無限に続きますが、例えば
πにもいつか終わりがあったとしてその最後の数が例えば【3】だったとした場合、πは3.14・・・(最終の数が2)以上
3.14・・・(最後の数が4)以下の長さとなるのですか?
円の周の長さと円の面積を求める式ではどう違いますか?
使うのは同じπだよ〜
中学校で習った記号を使って円の面積の式を教えてください
公式でいうとr2×πですか?
そうだね
質1 6×π+9は、6π+9に省略していいか?
質2 7×π(単位) (単位)に等式ではないから単位はつけていいか?
>質1 6×π+9は、6π+9に省略していいか?
いいよ
>質2 7×π(単位) (単位)に等式ではないから単位はつけていいか?
いいよ
π×π=πのにじょうになりますか?
なるよ!
つまり、πは円周率(3.14…)の省略した記号ということですか?
そうだね!
1、4πa +3/5πa の答えは何ですか
2、4πab + 5ab の答えは何ですか
3、3πab × 4ac の答えは何ですか
6πってなんですか?
πを3.141592653589793238462643383279502884197169399375105820974944まで覚えたんですが、その先はどうやって覚えたらいいですか??
πは、約!3.14、ということですか?
2πとは、約6.28?
訳分からねぇ
答えが、3分の4×πになる問題があるんですけど3分の4πになってて×が略されてるんですけど×が略される意味は何ですか?なるべく早めに返信ほしいです、、、
使い方がわからないです。
どう使うん?
使い方がよくわからないです。
教えて!!