【1次関数の公式】変化の割合の求め方がわかる3つのステップ

一次関数の変化の割合の求め方がわからんねえ！

こんにちは！この記事をかいているKenだよ。本屋にいきたいね。

一次関数の問題で、

変化の割合をもとめろ！！

ってヤツがよくだされる。

こいつは、変化の割合の公式、

（変化の割合）＝（yの増加量）÷（xの増加量）

をつかえば攻略できるよ。

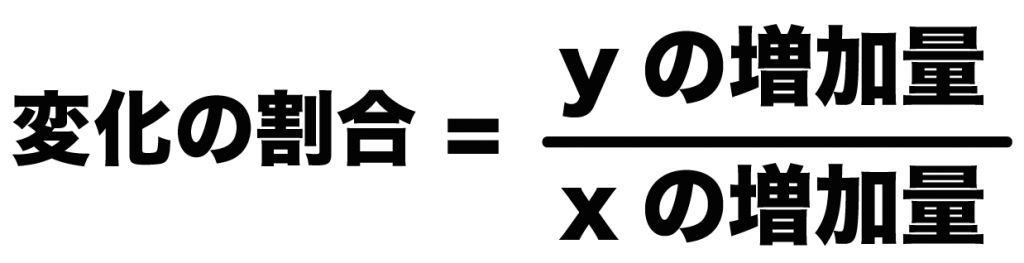
たとえば、

xの増加量が5のとき、yの増加量が25の関数があったとしよう。

こいつの変化の割合は、

(yの増加量)÷（xの増加量）
= 25 ÷ 5
= 5

になるんだ。

公式ならすぐ計算できちゃうでしょ？？

今日はこの公式を使って、

1次関数の変化の割合の求め方

を3つのステップで解説していくよ。

テスト前に参考にしてみてね^^

一次関数の「変化の割合」の求め方がわかる3ステップ

例題で「変化の割合」をもとめてみよう！

例題

xが3から6に変化したとき、yの値が8から-1になる一次関数があったとしよう。
この一次関数の変化の割合をもとめよ！

つぎの3ステップで攻略できちゃうよ！

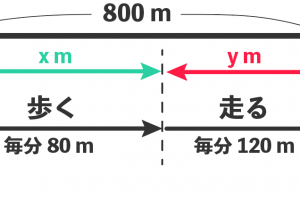
Step1. 「xの増加量」をもとめる！

まず「xの増加量」から計算しよう。

xの増加量の求め方は、

（変化の後のxの値）- （変化の前のxの値）

だ。

つまり、ゴール地点からスタート地点のxの値をひいてやればいいんだ。

例題では、

xの値は「3」から「6」 に変化したんだよね？？

ってことは、このときのxの増加量は、

(変化の後のxの値) – (変化の前のxの値)
= 6 – 3
= 3

になるよ！

Step2. 「yの増加量」を計算する！

yの増加量をもとめてみよう！

「yの増加量」も「xの増加量」とおなじで、

（変化の後のyの値）- （変化の前のyの値）

で計算できるよ。

例題をみてみよう。

yの値は「8」から「-1」まで変化してるよね？？

yの増加量を

（変化の後のyの値）- （変化の前のyの値）

で計算してやると、

-1 – 8
= -9

になるね。

yの増加量は「-9」ってことだよ。

勘の鋭いヤツはここで、

えっ。yの増加量がマイナスっておかしくね？？

って思うはずだ。

ぶっちゃけ、暴動がおきてもおかしくない。

ここで覚えておいてほしいのは、

増加量がマイナス（負の数）になる場合もありえる

ということだ。

xとかyの増加量ってただの表記であって、

かならずしもプラスになっているとは限らない。

増加量というより、

xとyの「変化量」と捉えたほうがわかりやすいかもね。

Step3. 「yの増加量」を「xの増加量」でわる！

xとyの増加量をゲットしたね？

あとは公式で計算してやるだけさ。

（変化の割合）＝（yの増加量）÷（xの増加量）

を使ってみてね。

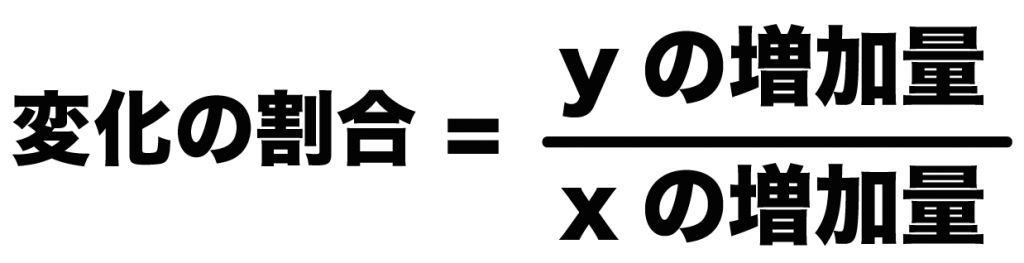
例題をみてみて。

xとyの増加量って、

• xの増加量：3
• yの増加量：-9

だったよね？？

こいつらを公式で計算してやると、

（変化の割合）
＝（yの増加量）÷（xの増加量）
=   – 9 ÷ 3
=   – 3

になるよ。

変化の割合は「-3」になったね。

つまり、

この1次関数はxが1増えるごとに、yが3減る野郎だってことさ。

変化の割合の意味がイマイチ・・・・

ってときは、

一次関数の変化の割合の記事で復習してみてね^^

まとめ：一次関数の変化の割合の求め方は公式で1発！

変化の割合の求め方はわかった！？

（変化の割合）＝（yの増加量）÷（xの増加量）

っていう公式で計算していこう。

問題をといて計算になれてみてね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。