【簡単公式】3秒でわかる！四角形の内角の和の求め方

四角形の内角の和の求め方がわからんぜ？？

こんにちは！この記事をかいているKenだよ。水道水、うまいね。

四角形の内角の和

ってたまに求めたいよね？？

そんなときは、

多角形の内角の和の公式をつかえば一発。

n角形の内角の和は、

180× (n-2)

で計算できちゃうんだ。

四角形の内角の和は、

nに「4」を代入してやればいい。

すると、

180× ( n -2 )
= 180 × (4-2 )
= 360°

って計算できちゃう！

つまり、四角形の内角の和は、

360°

になるんだ！！！

なぜ四角形の内角の和は360°になっちゃうの？？

でもさ、

なぜ四角形の内角の和は360°になるんだろう？？

便利すぎてこわいよね。。

せっかくだから、

内角の和が360°になる理由をさぐっていこう。

その理由はずばり、

四角形に「三角形が2つ」含まれているからなんだ。

対角線をすーーーっとひいてみよう。

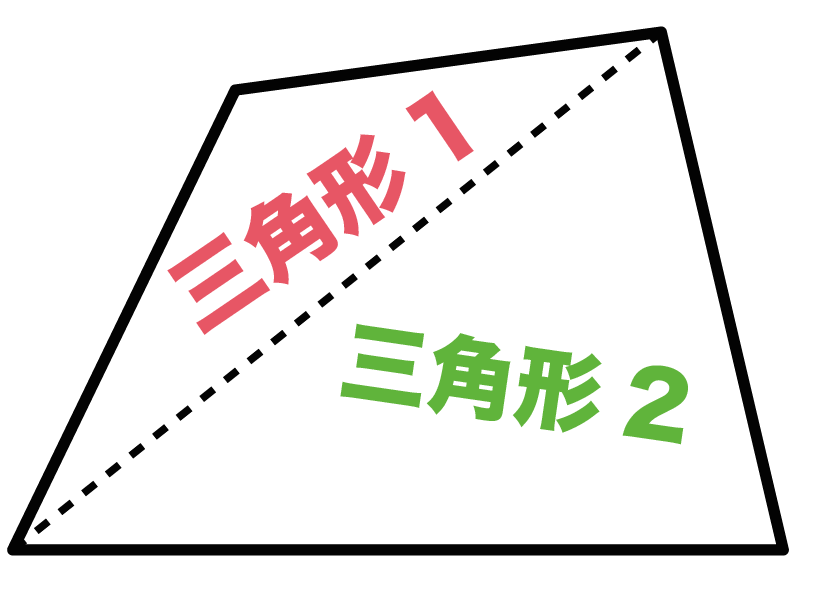
すると、

そこには、

三角形が2つ出現しているはず。

んで、

三角形の内角の和は180°だったよね？？

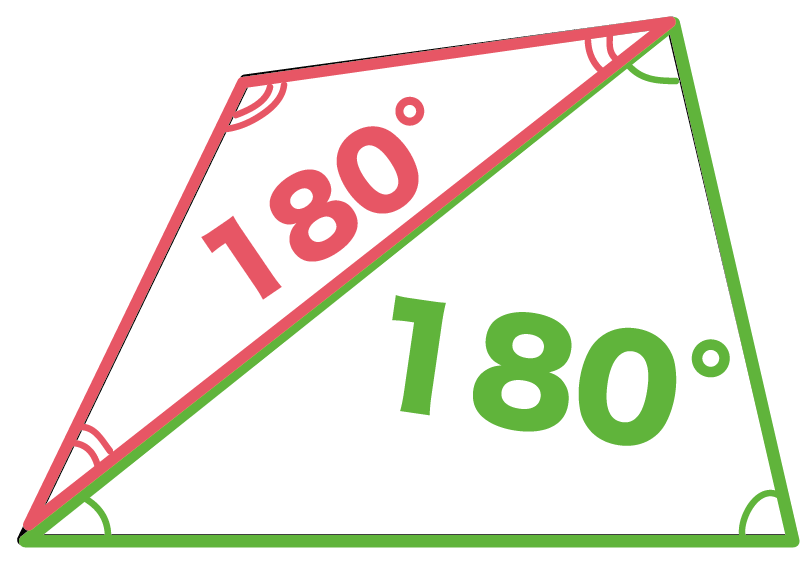
ってことは、

三角形が2つ隠れている四角形の内角の和は、

180°×2
= 360°

になるってわけ。

これで四角形の内角の和を計算できたね^_^

まとめ：四角形の内角の和は360°である！

多角形の内角の和を求めたいときは、

三角形が何個かくれているのか？？

を調べてみよう！

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。