一次関数の変域の応用問題を解きたい!
こんにちは!この記事をかいているKenだよ。汗かきたいね。
一次関数の変域の求め方の基礎はわかった。
だけど、ときどき、
変域の応用問題ってでてくるよね。
たとえば、つぎのような問題さ。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
いっけん楽勝にみえる。
だけどじつは、うっかりミスを誘うトラップ問題なんだ。
今日はこの変域の問題の解き方を3ステップで解説していくよ。
よかったら参考にしてみてね。
一次関数の変域の応用問題の解き方がわかる3ステップ
例題をいっしょにといていこう。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
Step1. 傾きの符号をチェックする
まずは問題で登場する、
一次関数の傾きの符号をチェックしよう!

傾きが+なのか??
それとも、とんでもなくマイナスなのか??
さらっと調べてみよう。
例題の関数の、
y = -2x + b
に注目してみて。
こいつの傾きは「-2」。
あきらかにマイナスがついちゃってるよね??
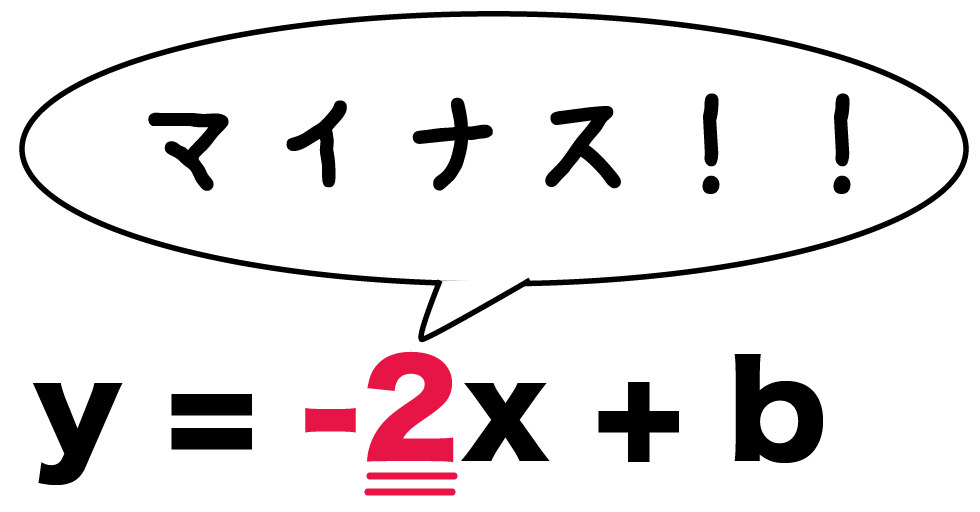
ってことで、例題の傾きは負の数だ。
Step2. 直線が通る2点を求める!
つぎは、
xが大きくなるとyはどうなるか??
を考えてみよう。
もし、一次関数の傾きが+のとき、
xが大きければ大きいほどyも大きいね?
だから、xが最大値になるとき、yも最大値になるってわけ。
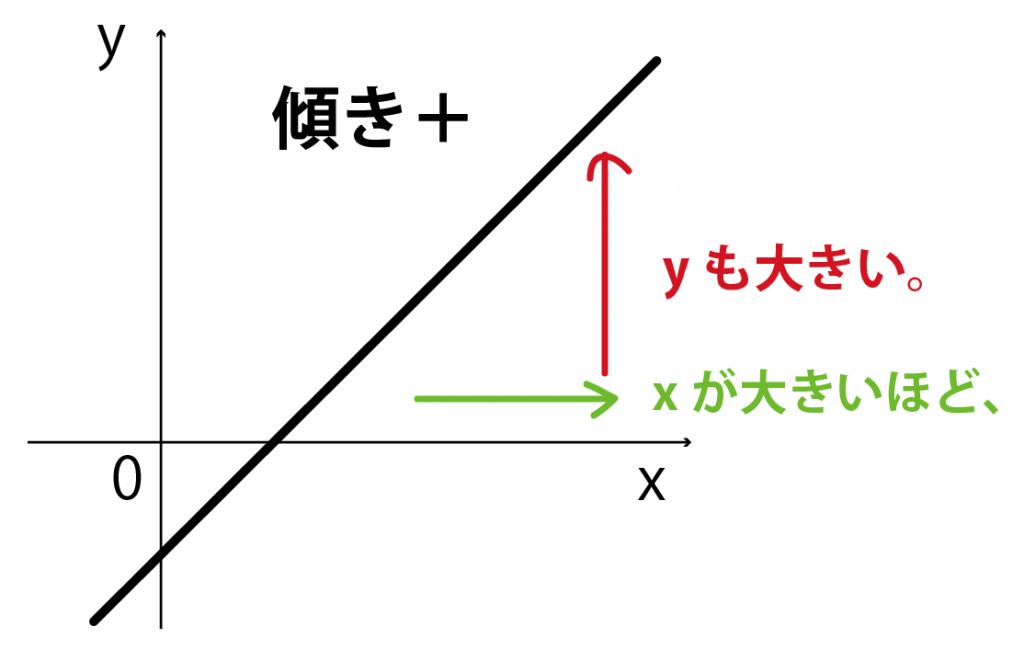
逆に、傾きが -のとき、
xが大きければ大きいほどyは小さくなっちゃう。
だから、xが最大値のときはyは最小値になるわけさ。

つまり、これをまとめるとつぎのようになる↓↓
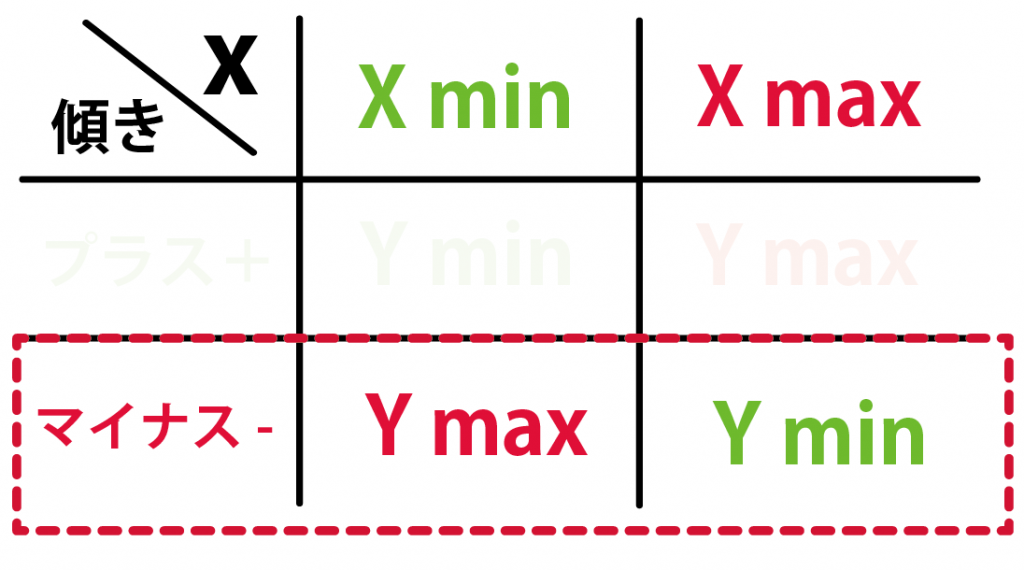
- 傾きが「+」: xが最大値のとき、yは最大値。xが最小値のとき、yは最小値
- 傾きが「−」: xが最大値のとき、yは最小値。xが最小値のとき、yは最大値
例題をみてみよう。
一次関数の傾きは「マイナス」だったよね??
xとyの変域から最小値・最大値をだしてみると、
- x: 最小値 = c, 最大値 = 4
- y : 最小値 = -5, 最大値 = 5
になってるね。
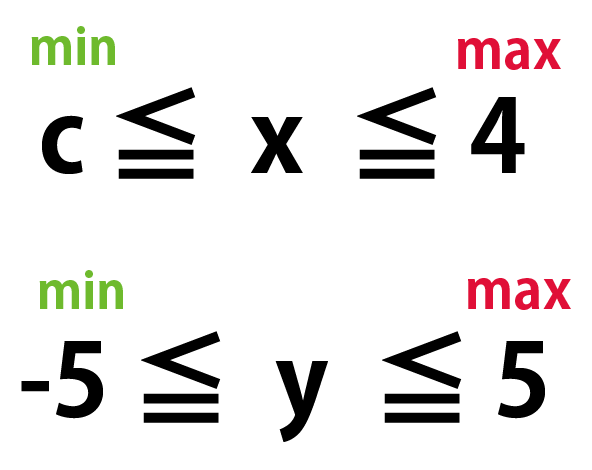
んで、一次関数の傾きがマイナスだから、
- xが最小値cのとき、yは最大値5
- xが最大値4のとき、yは最小値-5
になるんだ!

つまり、
y = -2x + b は、
- (c, 5)
- (4, -5)
の2点を通るんだ。
こんな感じで、
xとyの組み合わせをみつけるのが第2ステップだよ^^
Step3. 座標を直線の式に代入する!
最後は、2つの座標を式に代入してみよう。
例題の直線は、
- (c, 5)
- (4, -5)
の2点を通るはずだったね??
こいつを直線の式、
y = -2x + b
さっそく、y = -2x + bに(4, -5)を代入すると、
y = -2x + b
-5 = -2 × 4 + b
b = 3
になるね。
つぎは、bの値がわかった一次関数の、
y = -2x + 3
に(c, 5)を代入してcを求めてみよう。

すると、
y = – 2x + 3
5 = – 2c + 3
c = -1
になるよ。
これで文字の正体がわかったね。
- b = 3
- c = -1
おめでとう^^
まとめ: 一次関数の応用問題はグラフをかかなくても楽勝!
一次関数の変域の問題はよく、
グラフをかけば解ける
っていわれる。
だけどね、ぶっちゃけグラフなんていらん。
傾きの符号をみて、xとyの組み合わせを考えればいいんだ。
応用問題におそれず挑んでいこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。

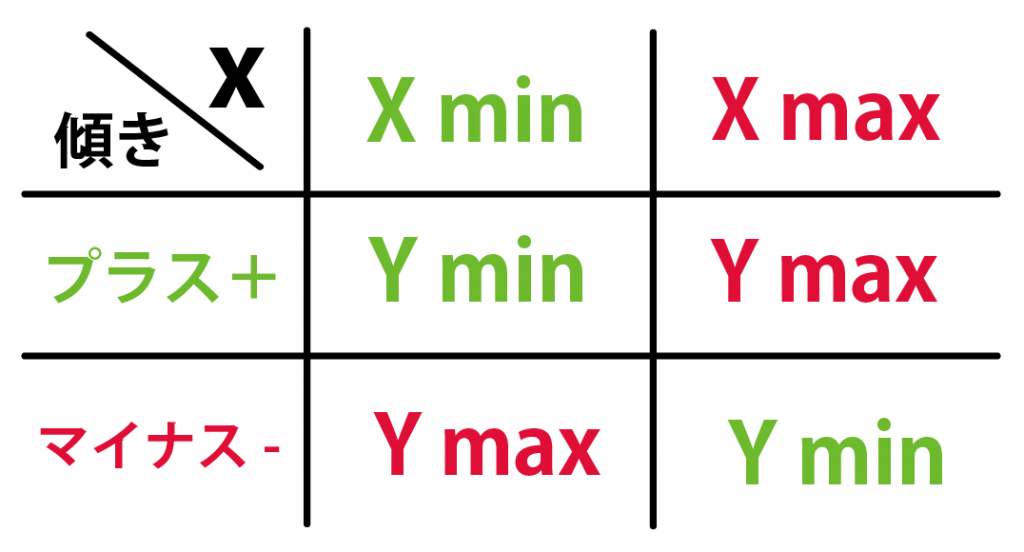
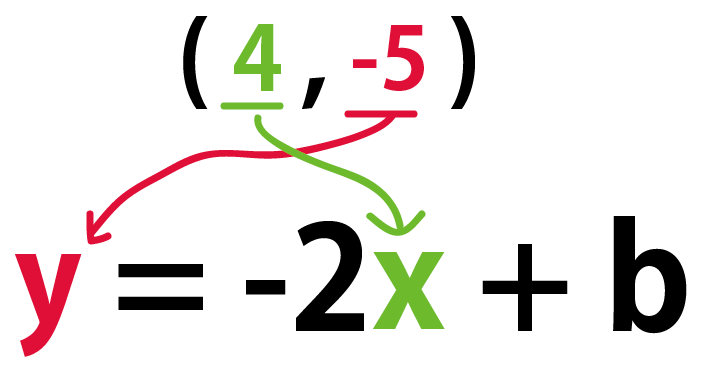





一次関数 Y= -3x+2 についてxの変域が x≧ 0 の時のyの変域を求めなさい。
A. Y≦2
………………………………………………
この問題なのですが、なぜ答えの
不等号が違うんですか
>一次関数 Y= -3x+2 についてxの変域が x≧ 0 の時のyの変域を求めなさい。
一次関数の変域の問題は実際にグラフをかいてみるといいよ。
符号が違うのは、傾きがマイナスだからね。
y=2x−1でxの変域がy≧3とき何になるんですか?
>y=2x−1でxの変域がx≧3とき何になるんですか?
変域の問題はグラフをかいてみるといいよ。
xが3以上の時、yはどうなってるかな?
次の一次関数y=ax+bを求めなさい。
a<0でxの変域が-1≦x≦2の時のyの変域が3≦y≦9である。
という問題で、なぜx=-1のときy=9になって、x=2のときy=3になるんですか?
>次の一次関数y=ax+bを求めなさい。
a<0でxの変域が-1≦x≦2の時のyの変域が3≦y≦9である。
という問題で、なぜx=-1のときy=9になって、x=2のときy=3になるんですか?
グラフをかいてみるとしっくりくると思うんだけど、
傾きがマイナスの時は、xが大きいほどyが小さくなるよね?
ってことは、xが最大値2の時、yは最小値3になるんだ。
そのまた逆も然りだ
y=-4X+5
1.4.16.64(g)の重りが3個ずつある。重りを組み合わせて99gの重さにするとき、重りは全部で何個使うか。
一次関数に関係なくてすみません><この問題で、四進法の考えを使えば答えを導き出せるのはなぜですか?
一次関数y=ax+6でxの変域が0≦x≦3の時のyの変域は3≦y≦6であるaの値を求めなさい。
という問題は、どう解けばいいですか?
>一次関数y=ax+6でxの変域が0≦x≦3の時のyの変域は3≦y≦6であるaの値を求めなさい。
という問題は、どう解けばいいですか?
x=0の時はyは切片6になるはず。
yが6になってるのは最大値だから、xが最小値0の時yが最大値6ってことになる。
つまり、このaは負の数で、あとは残りの変域を代入してaを求めてみよう
y=ー3xで、xの値が1からmまで変化するときの変化の割合がー15である。このとき、mの値はいくらか。
教えてください。
一次関数y = axー2のグラフは、点(6,6)を通る。x=3のグラフときのyの値はなんですか?
>一次関数y = axー2のグラフは、点(6,6)を通る。x=3のグラフときのyの値はなんですか?
(6,6)を代入してaを求めてみよう。
aが求まったらx=3を代入してその時のyを求めてみよう
1次関数y=-2x+aにおいて、定義域がa≦x≦1であるとき、値域がb≦y≦2となるように、定数a,bの値を定めなさい。
という問題が、どのように解けばいいのかが分かりません。教えてください。
>1次関数y=-2x+aにおいて、定義域がa≦x≦1であるとき、値域がb≦y≦2となるように、定数a,bの値を定めなさい。
図を書くとわかりやすいよ。
傾きがマイナスの場合は、xが最大値のときはyが最小値、
逆にxが最小値のときはyが最大値になるはずだ
変化の割合と定義域って同じですか?
>変化の割合と定義域って同じですか?
一次関数でいうと、変化の割合は傾き、定義域はxの変域のことだ!
ずっと分からなかったけど教え方がわかりやすくて理解出来ました!テスト頑張ります!
>ずっと分からなかったけど教え方がわかりやすくて理解出来ました!テスト頑張ります!
ありがとう!頑張ろうぜ!!
中間テストマンさんの答えってa=1ですか?
期末テストでこのような問題が出たのですが‥
kenさんの答えを見てなんとなく理解したと思ったのですが、代入してみると片っぽは合っていてもう片っぽは違うんです。よく分からないので、詳しく教えて頂けませんか?計算式もあると有難いです。
よろしくお願いします
>中間テストマンさんの答えってa=1ですか?
期末テストでこのような問題が出たのですが‥
kenさんの答えを見てなんとなく理解したと思ったのですが、代入してみると片っぽは合っていてもう片っぽは違うんです。よく分からないので、詳しく教えて頂けませんか?計算式もあると有難いです。
a=-1になるはず。
x=3の時y=3を代入してみればいいね
ゆりかさんの、答えってなんですか?
この単元のテストが月曜日にありまして、応用の解いているのですが解けなくて……
答えをなるべく早めに教えて下さると嬉しいですo(_ _)oペコリ
お忙しいのにすみません
よろしくお願いします。
図形の変域の求め方ってどうやって求めるんですか?
また、xもyも変域が出ていない場合、どうしたらいいんですか?
一次関数の利用の動点の問題かな?
xとyの変域は一次関数の式が変化するごとに変わってくるね
2つの関数y=x+6とy=ax^のxの変域が-6≦x≦3のときにyの変域が同じになる。このとき、の値を求めよ。
この問題の解き方を教えてください。
まずはy=x+6の-6≦x≦3のときにyの変域を求めてみよっか
y=1/2x+1(-2≦x≦1)のyの変域と、y=Ax2乗(-2≦x≦1)の変域は同じである。
yの変域 0≦y≦3/2
A の値を求めなさい