二次関数で三角形の面積を計算しろ??
やあ、ぺーたーだよ。
二次関数のテストでよくでるのは、
三角形の面積を求める問題。
難しいからみんな嫌がるよね??
図形と関数のコラボとかやめてほしいけど、
テストに出てきちゃう。
何とか解けるようにしたいね。
そこで、今日は、
二次関数の三角形の面積の求め方
を3ステップを紹介するよ!
二次関数で三角形の面積を求める4ステップ
つぎの問題をといてみよう!
y = 1/2 x² のグラフ上に2点A, Bがあり、
それぞれのx座標は-4と2です。
直線ABとy軸の交点をCとするとき△AOBの面積を求めてください。
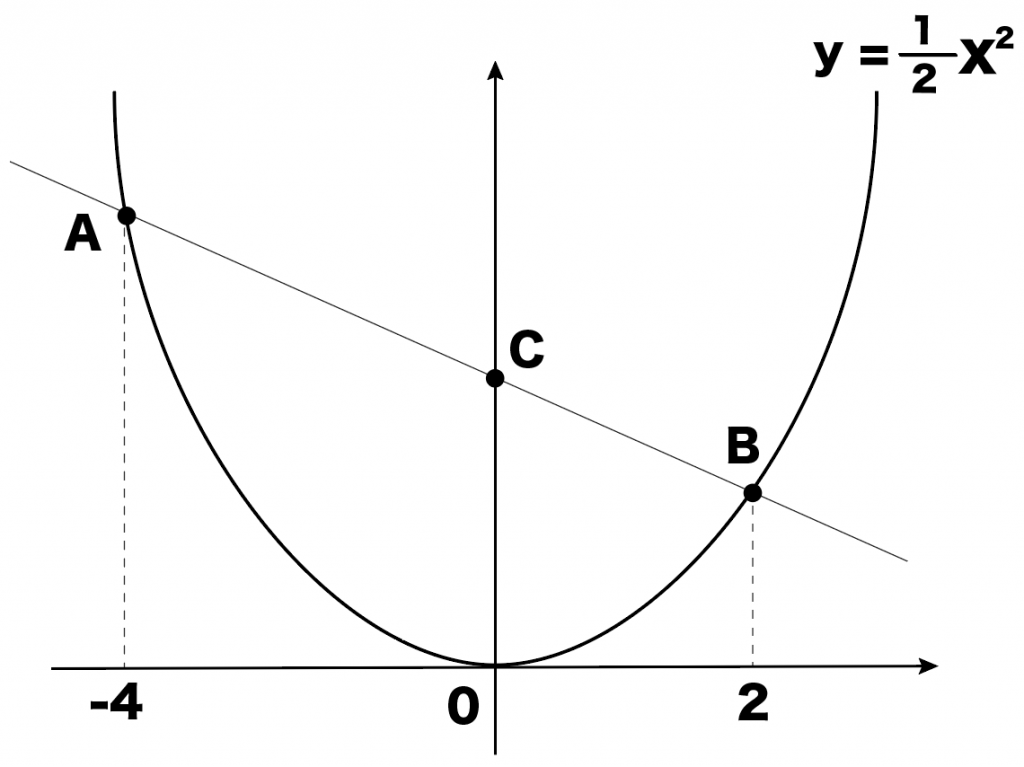
3ステップでとけちゃうよ。
- 座標を求めよう
- 三角形を二つに分けよう
- 二つ三角形の面積を求めよう
Step1. 座標を求めよう
まず座標を求めてみよう。
練習問題でいうと、
- 点A
- 点B
- 点C
の3点の座標ね。

この問題では、それぞの点のx座標がわかってる。
だから、
二次関数にxを代入すればいいね。
y = 1/2 x²にそれぞれ代入すると、
- 座標Aのy座標: y = 1/2 ×(-4)×(-4)= 8
- 座標Bのy座標: y = 1/2 × 2 × 2 = 2
になる。
ってことは、
- 座標A:(-4, 8)
- 座標B:(2, 2)
になるはずだ。
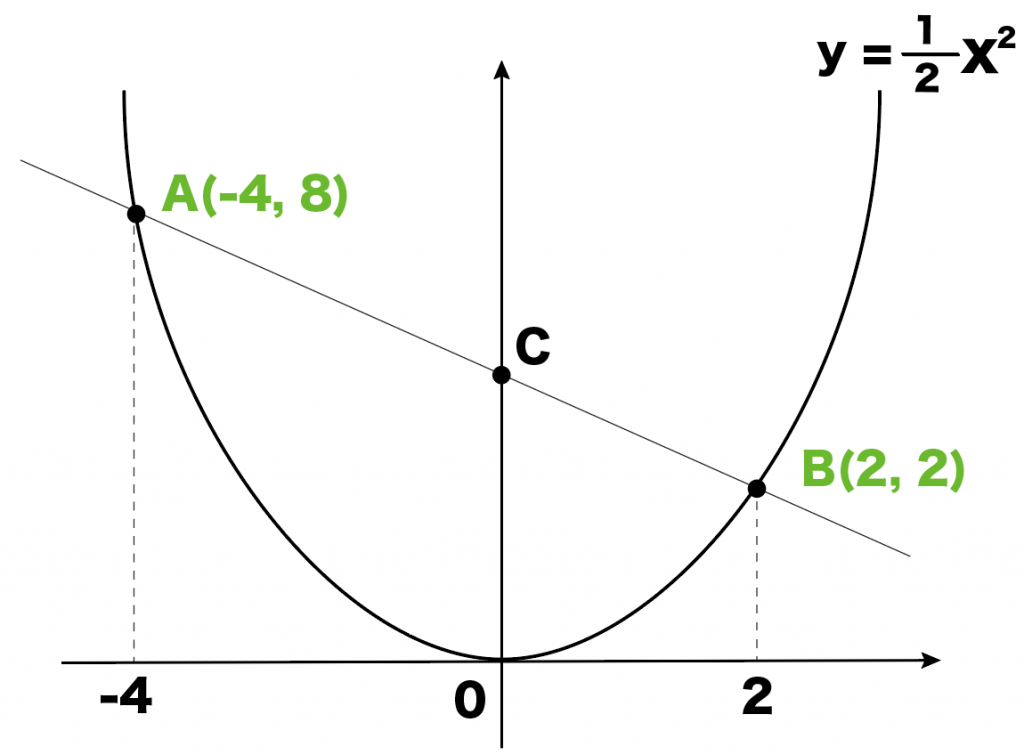
あとは点C。
こいつは、直線ABの切片だね??
直線ABの式がわかればCの座標もわかるってわけ。
直線ABの式は2点は、
- 点A(-4, 8)
- 点B(2, 2)
だ。
y=ax+bに代入して連立方程式をつくると、
8 = -4a + b
2 = 2a + b
ってなる。
こいつをとくと、
- a = -1
- b = 4
になるね。

つまり、直線ABの式は、
y = -x + 4
になるんだ。
点CはABの切片だから、
C (0, 4 )になるね。
ちょっと長くなったけど、分かった座標を図に書き込むよ!
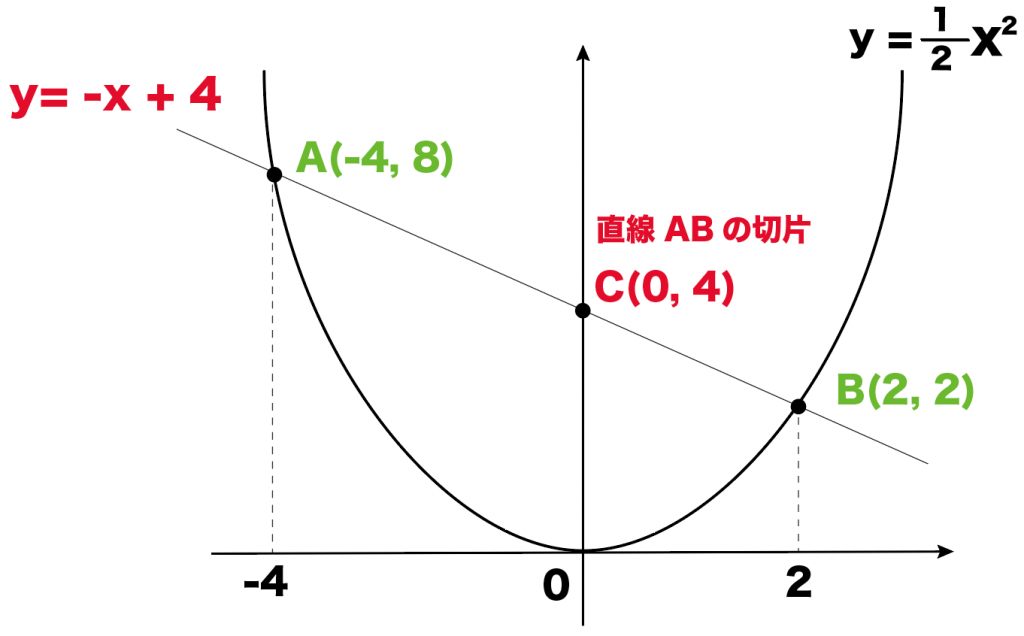
Step2. 三角形を2つにわける!
三角形の面積を2つにわけて考えてみよう。
練習問題では、
△AOBの面積
を求めたかったよね??
だがしかし、
そんな三角形見当たらない。
だから自分で、
△AOBを書き込むんだ。
すると、こんな三角形ができあがるよ!
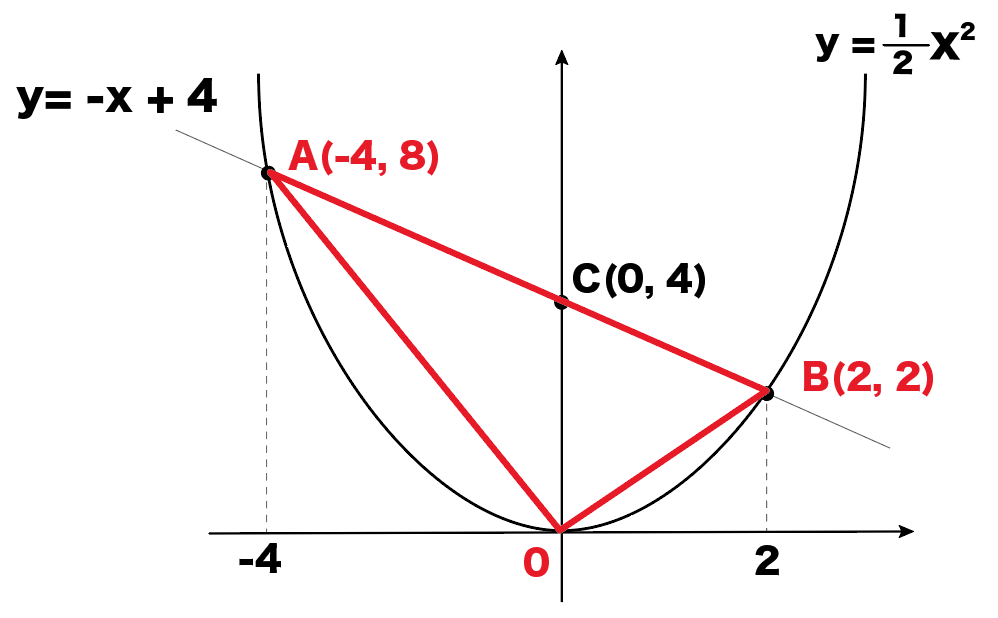
さあ、これで三角形の面積を求めよう!
…と言いたいところなんだけど、このままだと難しいんだ。
なぜなら、
底辺も高さもわかってないからね。
じゃあどうすればいいの!?
よーく見ると三角形が見えてこない?
そう!
△AOBで見るんじゃなくて、
三角形を2つに分けて考えるんだ!
どう分けるかというと…
△COAと、
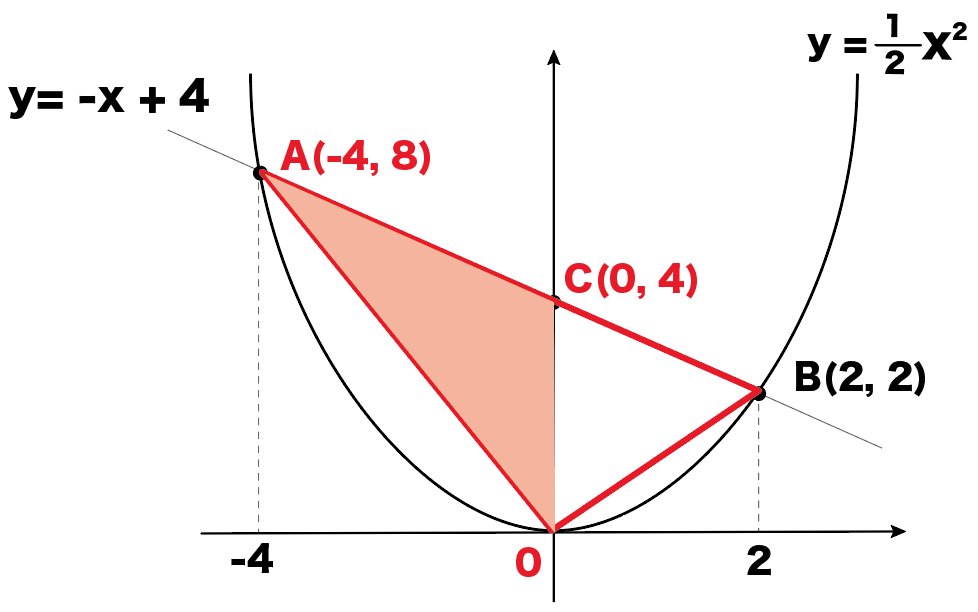
△COBでわけるんだ。
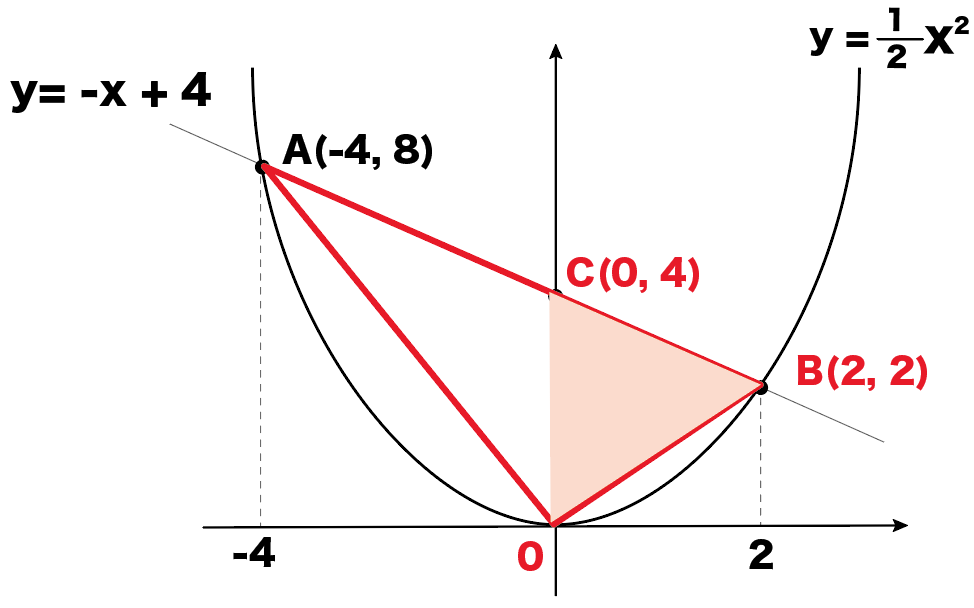
Step3. それぞれの面積を計算
三角形の面積を計算しよう。
わけた2つの三角形の面積をそれぞれ計算すればいいのよ。
まず△COAの面積。
COを底辺、Aのx座標を高さとしてみてね。
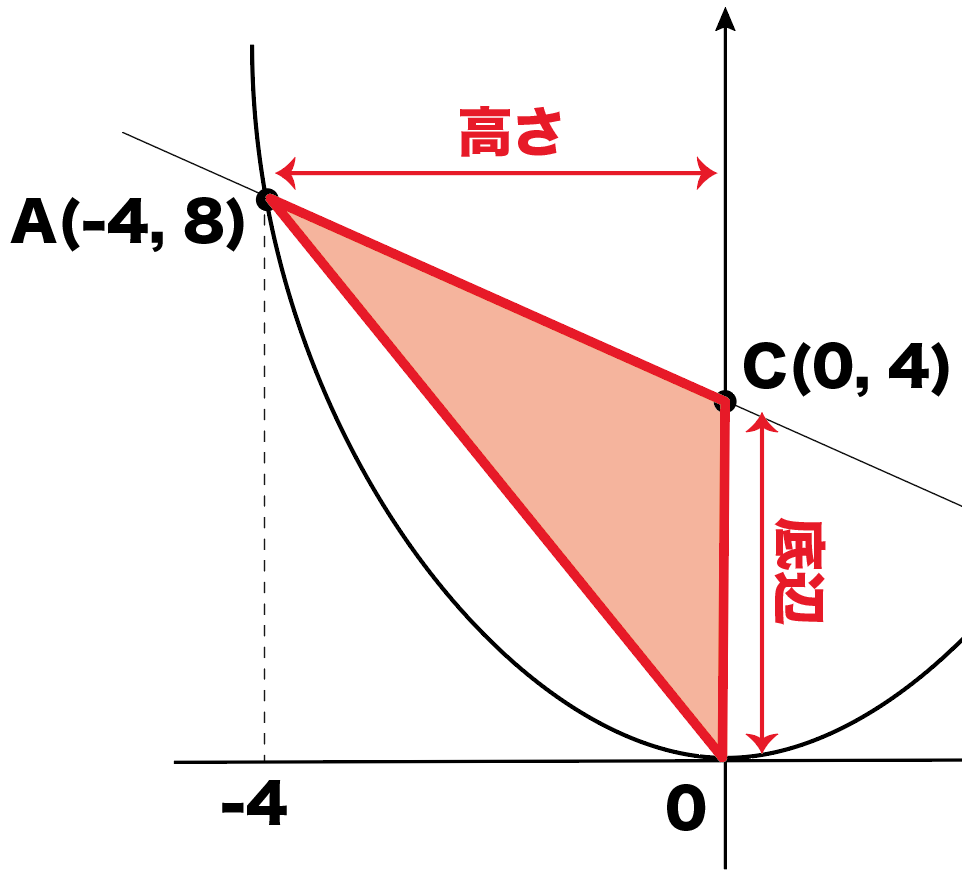
Oのy座標は0、Cのy座標は4だから
底辺=4。
高さは「Aからy軸まで」の長さ。
つまり、Aのx座標のことだから、
高さ=4だね。
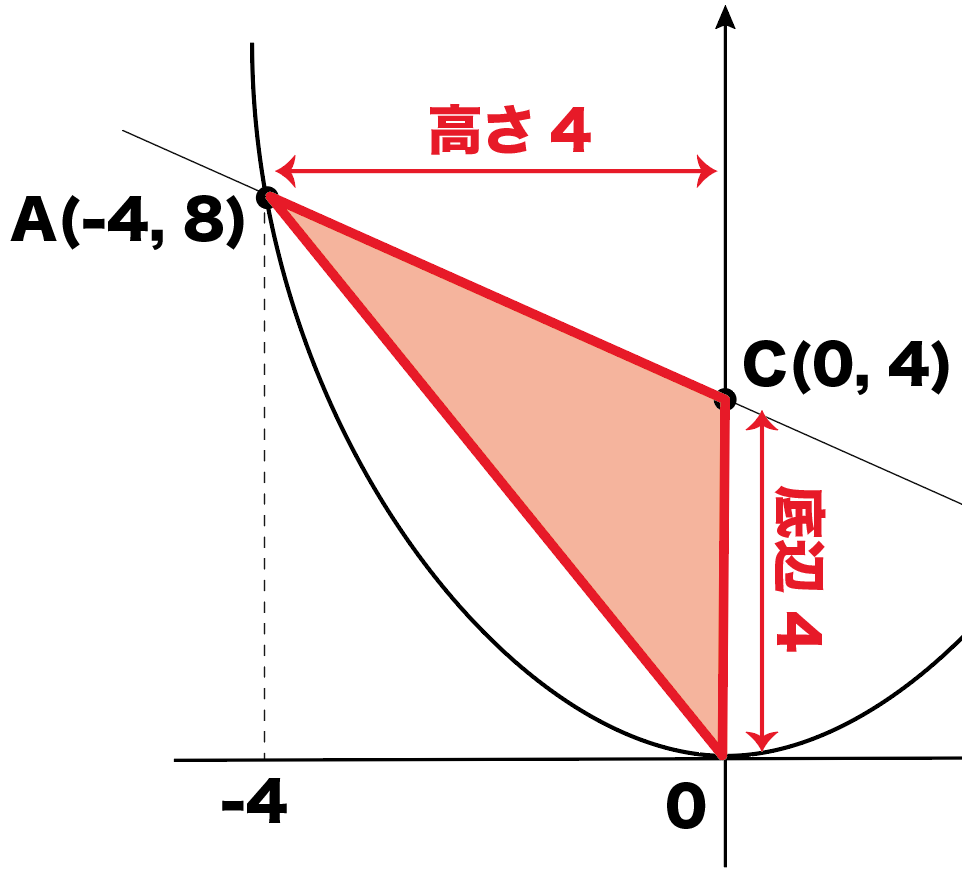
三角形の面積の公式は「底辺×高さ÷2」だったよね??
こいつで計算してやると、
△COA
= 底辺×高さ÷2
= 4×4÷2
= 8
になる。
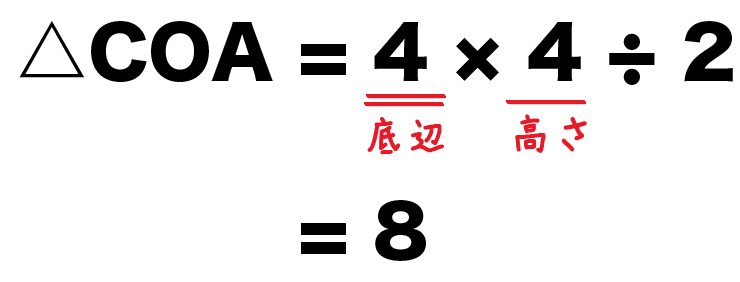
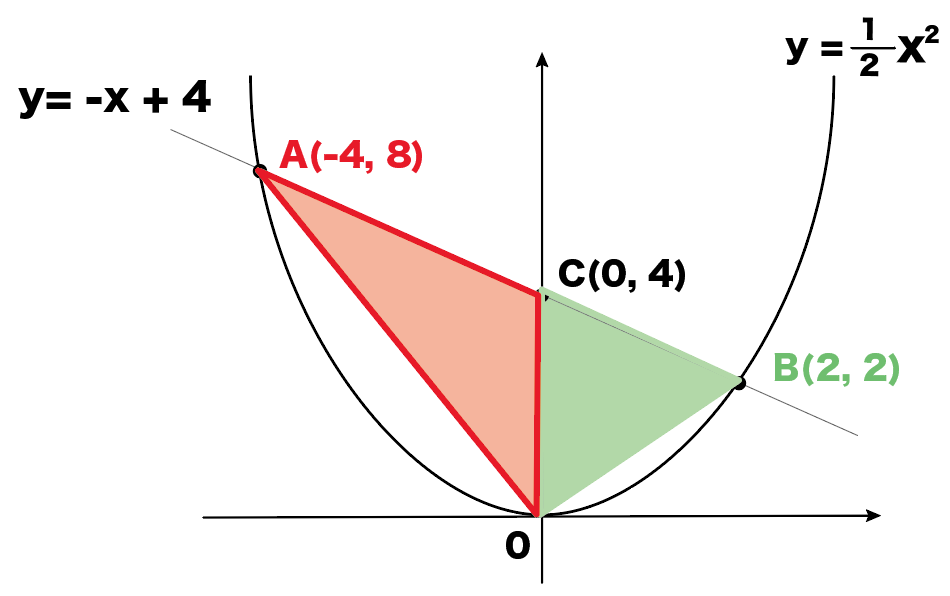
次は△COB。
COを底辺、Bからy 軸までを高さと考えてみると、

△COB
= 底辺×高さ÷2
= 4×2 ÷2
= 4

になるね。
Step4. 三角形の面積をたす
2つの三角形を足しちゃえば終わり!
練習問題でいうと、
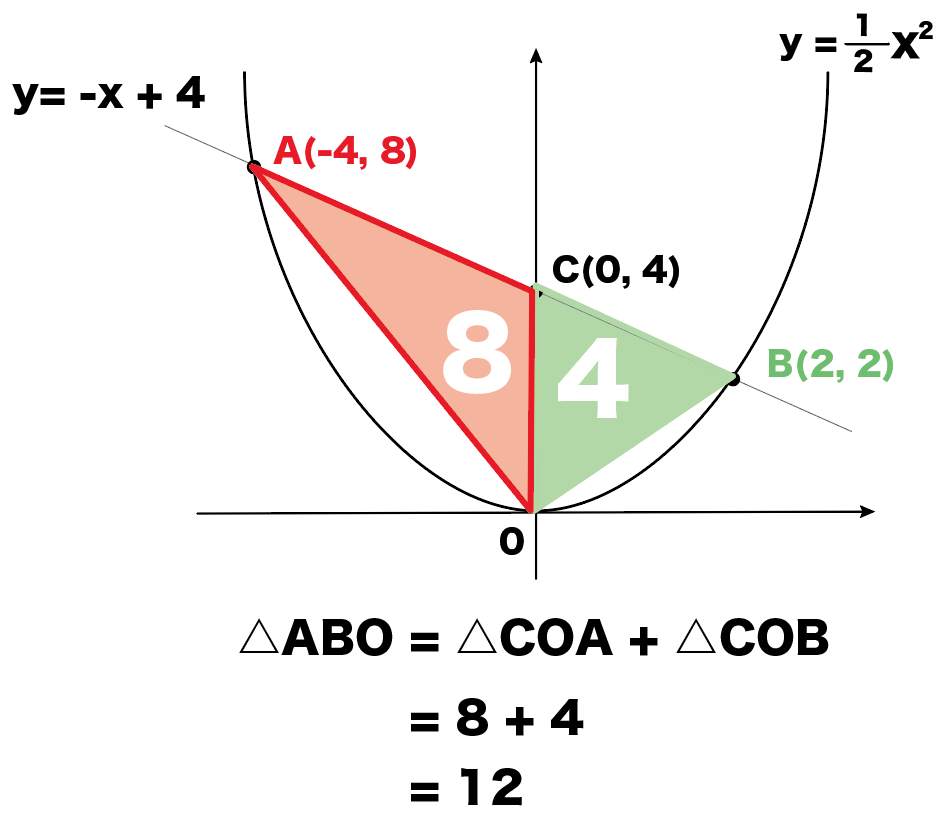
△AOB = △COA + △COB
ってわけだね。
実際に計算してみると、
△AOB
= 8 + 4
= 12
になる。
だから答えは12なのさ。
大変だったね。お疲れさま!
まとめ:二次関数の三角形の面積はわけて計算!
二次関数で三角形の面積を求める問題は、
- 座標を求める
- 三角形を分けて考える
の2ステップで大丈夫。
難しいけど、慣れれば絶対に解けるようになるよ。
じゃ、今回はここまで。
じゃあねー
ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める





A座標が(-2・-1)でB座標が(6・-9)の直線の
長さはどう求めますか?
放物線 y=2分の1x二乗
,直線y=3x-4の交点をA・Bとする
原点Oと、A・Bの三角形の面積の求め方を教えてください
どこを底辺にしますか!?
>A座標が(-2・-1)でB座標が(6・-9)の直線の
長さはどう求めますか?
この手の問題は図を書いてみるとわかりやすいよ。
AとBを頂点とする直角三角形をかいてみよう。
詳しくは「三平方の定理で座標上の2点間の距離を求める」
>放物線 y=2分の1x二乗
,直線y=3x-4の交点をA・Bとする
原点Oと、A・Bの三角形の面積の求め方を教えてください
これはy軸を底辺にして、2つの三角形に分けて計算したほうがいいかも
A座標が(4,4)
B座標が(-6,9)
この時の面積を求めたら
回答と違ったのですが…
>A座標が(4,4)
B座標が(-6,9)
この時の面積を求めたら
回答と違ったのですが…
例題と同じように2つの三角形にわけてみよう。
そのためには直線ABの切片を求める必要があるね
「△AOBの面積を二等分する
直線の式を求めよ」
なんて問題をたまに入試などで
見かけるのですが
解き方がよくわかりません
解き方を教えてください
>「△AOBの面積を二等分する
直線の式を求めよ」
なんて問題をたまに入試などで
見かけるのですが
解き方がよくわかりません
解き方を教えてください
面積を二等分する問題は、
1. 三角形の頂点
2. 頂点の向かい側にある辺の中点
の2つの点を通る直線の式を求めればいいね
なんでy=ax + bに代入するの?
>なんでy=ax + bに代入するの?
ABが直線ってことは一次関数だね。
だから一次関数の式y=ax+bに代入してるよ
たまに、問題で三角形の面積を求めてから面積比を求める問題があるのですがどうやって求めれば良いですか?
>たまに、問題で三角形の面積を求めてから面積比を求める問題があるのですがどうやって求めれば良いですか?
面積比の求め方は単純で、2つの三角形の面積を比にしてやればいいよ。
たとえば、三角形Aの面積が1, 三角形Bの面積が2の時は1:2の面積比になるね
「 y軸上に点Pをとる。△APBの面積と△ADBの面積が等しくなるとき、点Pの座標を求めなさい。」
というような問題の解き方を教えてください。
複数の質問申し訳ございません(´・_・`)
> y軸上に点Pをとる。△APBの面積と△ADBの面積が等しくなるとき、点Pの座標を求めなさい。
平行線と面積を使うね!
底辺をABで共有していて高さが等しい三角形は面積が等しいってやつ。
ABに平行な直線で、かつ、Dを通る関数を求めてみよう
このときCを通り、△OABを2等分する直線の式はどうなりますか?
最後のお疲れ様、でなんだか報われた気がしました。そんなこと言ってくれる人周りにいないから、
ありがとうございます いつも助かってます
関数y=x²について、xの変域がー2≦x≦4のとき、yの変域を教えてください。
>関数y=x²について、xの変域がー2≦x≦4のとき、yの変域を教えてください。
xの変域で0を含んでいる問題はちょっとトリッキーだ。
比例定数が正の数の時、yの最小値が0になることに注意してみよう。
詳しくは「二次関数の変域」を読んでみて
Y=ax+bにそれぞれ代入した時その形だと解きにくいので符号変えて解くことって可能ですか?
y=x/12と言う例とは異なったグラフの場合どうすれば良いのですか?基本解き方は同じですか?
だいたい一緒だよ!困ったら小さな三角形に分けて面積を求めて足し合わせてみよう
y軸を軸として一回転する立体などの問題が入試で出る傾向にあるのですが、手順がよくわからないです。教えてください、
回転体の問題の解き方を読んでみて!
△AOB=△APBの時、点Pの座標を求めよという問題で、二次関数の式はy=x2乗
一次関数(直線AB)はy=x+6で
点Aの座標は(-2,4)点Bの座標は(3,9)で、
点Pは二次関数のグラフ上にあります。
これは等積変形を使ってあげよう。
底辺ABを共有している三角形だから、面積が等しいってことは高さが同じなはず。
で、そのためにはABとOPが平行になっているよ
放物線y₌kx2上に、2点A、Bがあり、点Aの(-4,8)である。点Aと点B(2,2)のⅹ座標の比は2:1で、直線の比は2:1で直線ABとy軸との交点をC(0,4)とする。点Aからx軸に垂線を引き、交点Dとし、点Bからx軸に垂線を引き、交点Eとする。このとき四角形ABEDの面積kを用いて表しなさい。
まずはkを求めてやろう。
あとは四角形ABEDは台形だから面積を公式で求めて、そいつをkで表してやりゃいいね
放物線が下を向いていても解き方は変わりませんか
質問ではないですがとても分かりやすくて
解けた時めっちゃくちゃうれしかったです!
ありがとうございます!