【平方根の計算】ルート分数の割り算の仕方がわかる3ステップ

ルート分数の割り算の仕方？？

こんにちは！この記事をかいているKenだよ。健康はマジ大事だね。

ルートでやっかいなのは、

平方根の分数の計算だ。

なぜなら、

平方根を簡単にしたり、

分母を有理化したりで忙しいからね。

ルートの分数の計算なんて解きたくないぜ。

今日はそんなちょっとやっかいな、

ルート分数の割り算の計算方法

を4ステップで解説していくよ。

よかったら参考にしてみて^^

平方根の分数の割り算の解き方の4ステップ

ルート分数の割り算は4ステップだ。

1. 掛け算になおす
2. 約分する
3. 掛け算する
4. ルートを簡単にする

例題をといてみよう。

例題

つぎのルート分数の割り算をしなさい。

5分の√20 ÷ √(15分の2)

Step1. 掛け算になおす

まずは、割り算を掛け算になおそう。

ルート分数の割り算なのに、はやくも÷にバイバイ。

寂しいけどね、仕方ないんだ。

割り算を掛け算になおす方法は1つ。

それは、

「÷」を「×」にして分母と分子を入れ替えるのさ。

例題でもおなじ。

まず、「÷」を「×」にしちゃって、

「÷」のうしろの「√(15分の2)」の分子と分母をいれかえる。

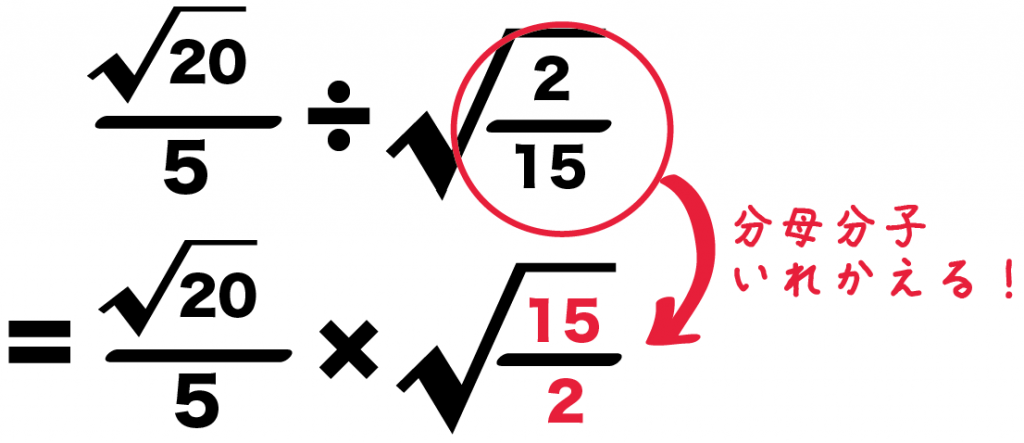
すると、

5分の√20 ÷ √(15分の2)
= 5分の√20 × √(2分の15)

になるね。

Step2. 約分する

つぎは約分だ。

分母と分子に公約数があったら約分しよう。

例題の計算式をよくみて。

5分の√20 × √(2分の15)

「5分の√20」の分子の「√20」、「√(2分の15)」の分母の「√2」に公約数があるね。

そう、√2だ。

ってことは、こいつらを√2でわれるから、

5分の√20 × √(2分の15)
= 5分の√10 × √(1分の15)

になる。

Step3. 分母・分子どうしを掛け算

分母・分子どうしで掛け算しよう。

ルートの掛け算の仕方をつかってみてね。

例題でも、分母・分子それぞれ計算すると、

5分の√20 × √(2分の15)
= 5分の√10 × √(1分の15)
= 5分の√150

になる。

Step4. ルートを簡単にする

最後に、ルートを簡単にしてやろう。

いちばん最初にルートを簡単にしたほうがいいだろ？？

って思うかもしれない。

だけどね、分数の割り算の場合はそうじゃない。

なぜなら、

ルートの中身をガッツリ約分できる可能性あるからね。

簡単にするのは約分まで待ったほうがいいんだ。

例題では分子の「√150」を簡単にできそうだね。

なぜなら、

150のなかには「5の2乗」がふくまれてるからさ。

ってことは、5をルートの外にだせる。

すると、

5分の√150
= 5分の5√10
= √10

になるね。

おめでとう！

ルート分数の割り算もマスターだ。

まとめ：分数の割り算の計算ではルートを簡単にするのは最後！

平方根の分数の割り算はどうだったかな？？

ほかのルート計算とたいして変わらないね。

ちょっと違うのは、

ルートを簡単にするのをステイする

ってことだ。

ガッツリ約分してから簡単にしても遅くない。

じっくり分数の割り算をしていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。