二次関数y=ax2の比例定数の求め方がわかる3ステップ

二次関数y=ax2の比例定数を求める問題？？

みんな、元気にしてる？そらだよ☆彡

比例定数って何かおぼえてる？？

1年生のときにならった比例では、

y=ax

のaを「比例定数」といったね。

じつは、

3年生でならう二次関数y = ax2でもおなじ。

定数aを「比例定数」っていうんだ。

今日はy=ax2の比例定数aを求めてみよう。

たとえば、つぎみたいな問題だね。

二次関数y=ax2の比例定数を求める2ステップ

比例定数の求め方は2ステップ。

1. xとyをy=ax2に代入する
2. aにかんする一次方程式解く

例題をいっしょにといてみよう。

Step1. xとyを関数の式に代入

xとyを、関数の式に代入してみよう。

y = ax^2

にxとyをぶちこんでやればいいのさ。

練習問題では、

• x = 3
• y = 18

があたえられてたよね？？

二次関数y=ax2に代入してみると、

y = ax^2

18 = a × 3 × 3

9a = 18

になるね。

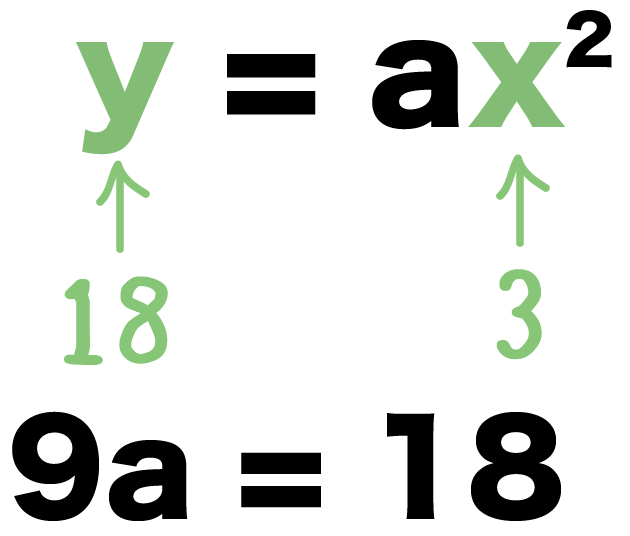
Step2. 一次方程式を解く

一次方程式をといてあげよう。

y=ax2にx・yをいれたら、aが残ったでしょ？？

あとは、aの1次方程式をとけばいいの。

練習問題では、

9a = 18

がでてきたよね？？

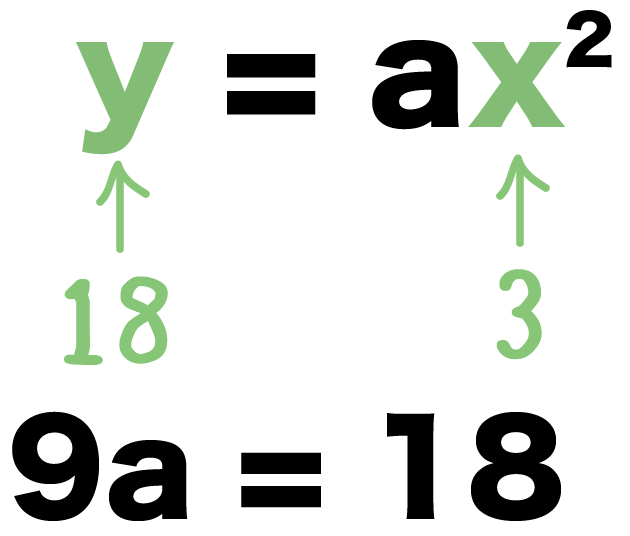
両辺をaの係数の「9」でわってやると、

9a ÷ 9 = 18 ÷ 9

a = 2

になるね。

おめでとう！

二次関数y=ax2の比例定数が求められたね^^

比例定数は「2」だ！

1点の座標がわかれば二次関数の式が求められる！

この問題のポイントは1つ。

それは、

関数y=ax2は1点の座標さえわかれば式を求められる

ってこと。

なぜなら、

xとy以外の未知数はaしかないからね。

xとyを代入しちまえば、aしか残らないってわけ。

解き方も簡単でうれしいね。

中学2年生でならった一次関数のときは、

グラフが通る2つの座標

が必要だったじゃん？？

一次関数の式は「y=ax +b」で未知数がaとbの2つあったからね。

それとくらべると、

二次関数y=ax2の比例定数は楽だね。

1つの方程式つくるだけでaがわかっちゃうからね。

問題をといてなれてみよう。

最後に練習問題を1つ紹介するね。

今日はここまで！

そんじゃねー

そら

そら

数学が大好きなシステムエンジニア。よろしくね！