一次関数と二次関数のグラフの違いって??
ある日、数学が苦手なかなちゃんは、
一次関数と二次関数のグラフをながめてました。


一次関数は久しぶりすぎて忘れかけてるし・・・・
二次関数はまだよくわからないところがある。
うわあっ!?
って、先生か。
びっくりした……
せっかくだから、
一次関数と二次関数グラフの違い
を見つけていこう!
復習もできるし一石二鳥??
そう!
さっそくみていこうー!
いぇーい
1次関数と2次関数のグラフの3つの違い
一次関数と二次関数のグラフの違いは3つあるよ。
- 次数
- 線の形
- yの値の符号
3つもあるんだ!
やべえー
どれもわかりやすいから大丈夫!
順番にみていこう。
はい!!
違い1. 「次数がちがう!」
まずは、一次関数と二次関数の、
「式」
を見比べよう!
あっ。
一次関数の式わすれちゃった・・・・
覚えてないのは仕方がない。
教科書見てみよう。

んー、違いかー!
bがあるかないかはわかったよ
もう一つの違いが注目ポイント!
あっ。
見つけた!
え!?
二次関数は、xが二乗になっている!

よく気付けた!
この2が二次関数の2なんだ!!
やったー!
つまり、
次数が違うってわけ!
へー
一次関数は一次式の関数、
二次関数は二次式の関数、
って覚えておくといいよ。
ってことは、もし、
三次式なら・・・
三次関数!?
そうそう!!
にやり
違い2. 「グラフの形」
相似記号の2つめの覚え方は、
グラフのかたち
だね。
かたち・・・
そうそう!
一次関数と二次関数のグラフをみてみて。

まっすぐと、
曲がってる感じかな?
そうだね。
一次関数が直線で、
二次関数が曲線!
これは、わかりやすい!
あー!そうそう!
一次関数は直線、
二次関数は放物線、
っておぼえておこうね。
うす!
違い3. 「yの値の符号」
最後はyの値について!
なんか、難しそう。
そんなことないよ!
ヒントはグラフに隠れているから!
グラフ?
あっ、そうか!!
一次関数だとyはプラスにもマイナスにもなる!
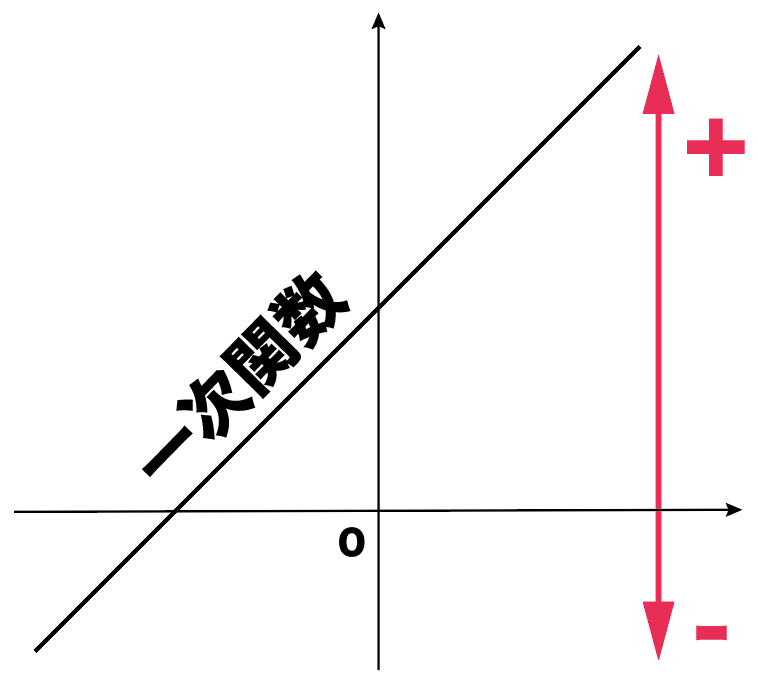
おー
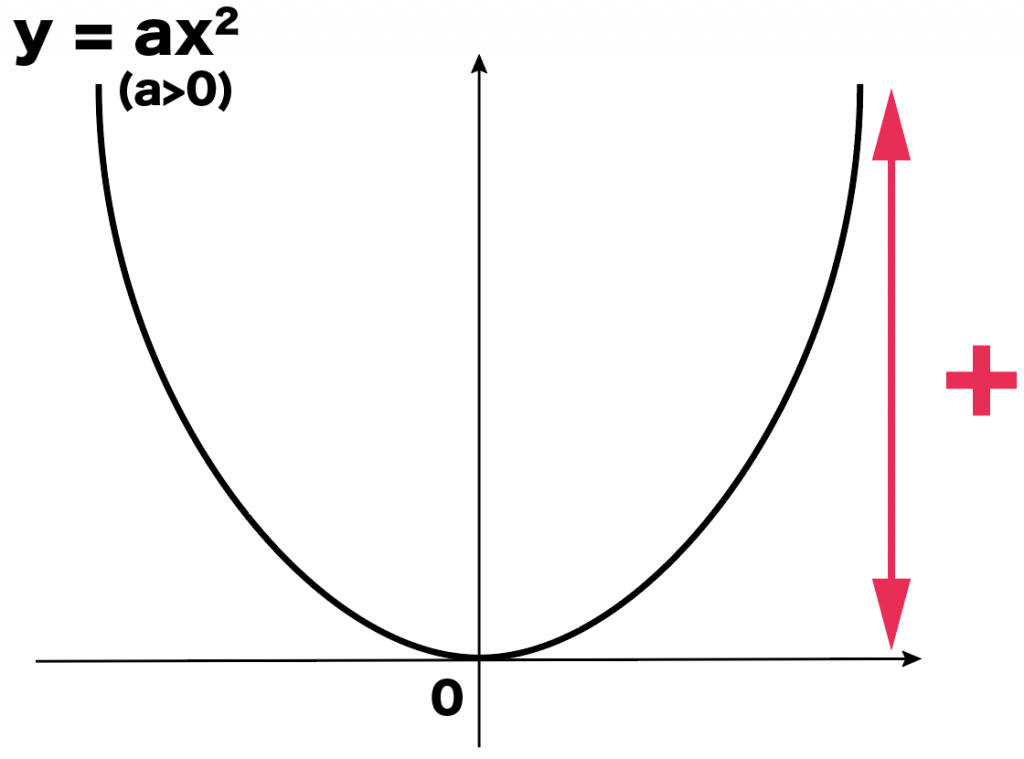
二次関数y=ax2だとどうなる??
二次関数y=ax2だと、
yの値がプラスだけのときや、
yの値がマイナスだけのときがある!
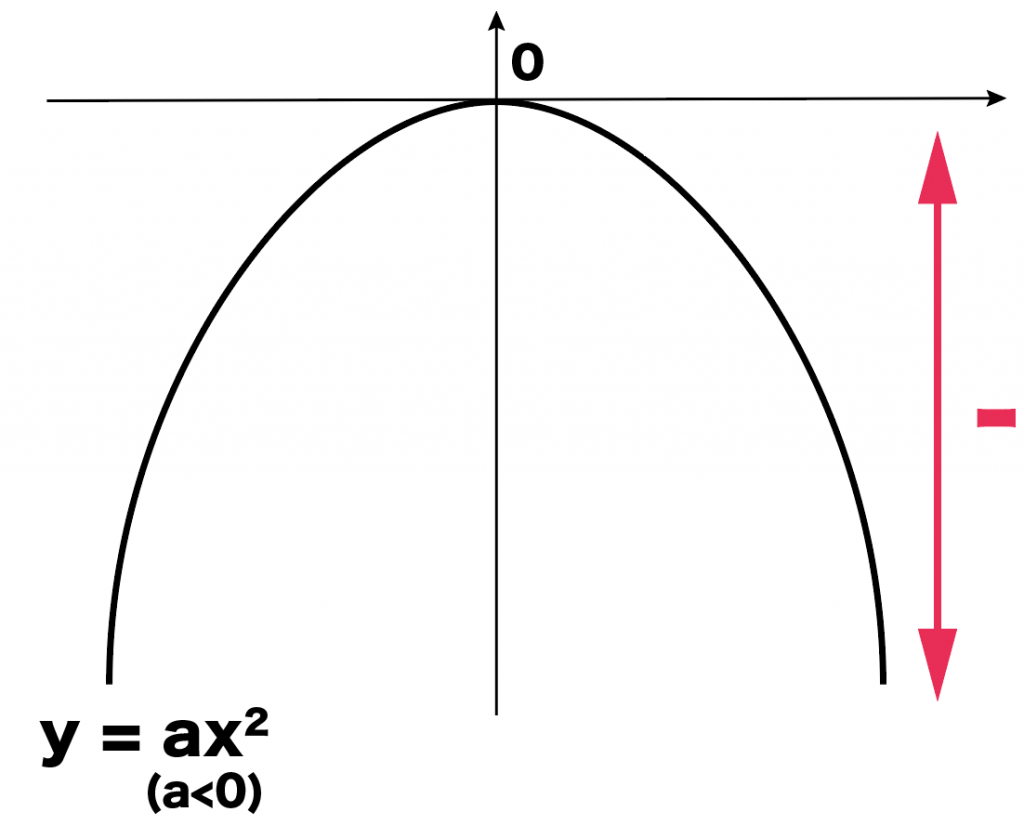
そうそう!
なんでだとおもうー?
えっと。。。
xが負の数でも二乗すると、
正の数になるから・・・?
そうそう!
例えば、y=x²だと……
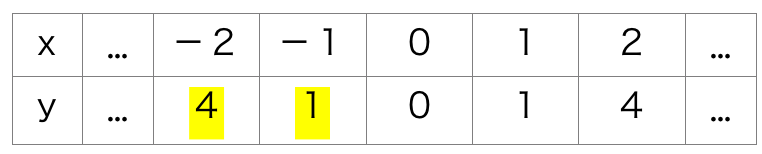
あっ、やっぱりそうじゃん!
うん、そうそう!
なんか、直線が魔法で曲げられたのかと思った
……!?冗談、だよね?
半分くらいは。
けど、二次関数のグラフが曲線になるか知れてよかった。
まとめ:1次関数と2次関数は次数もグラフも違うじゃん!
じゃあ、いつものまとめをしよう!
一次関数と二次関数のグラフの違いは、
- 次数
- グラフの形
- yの値のとりかた
だったね??
一次関数のことも思い出せてきたかも。
よかった。
一次関数と二次関数が
一緒に出てくる問題もあるんだ。
えっ、どんな??
2つの関数の交点を求める問題があるんだよ
なんか、難しそう。
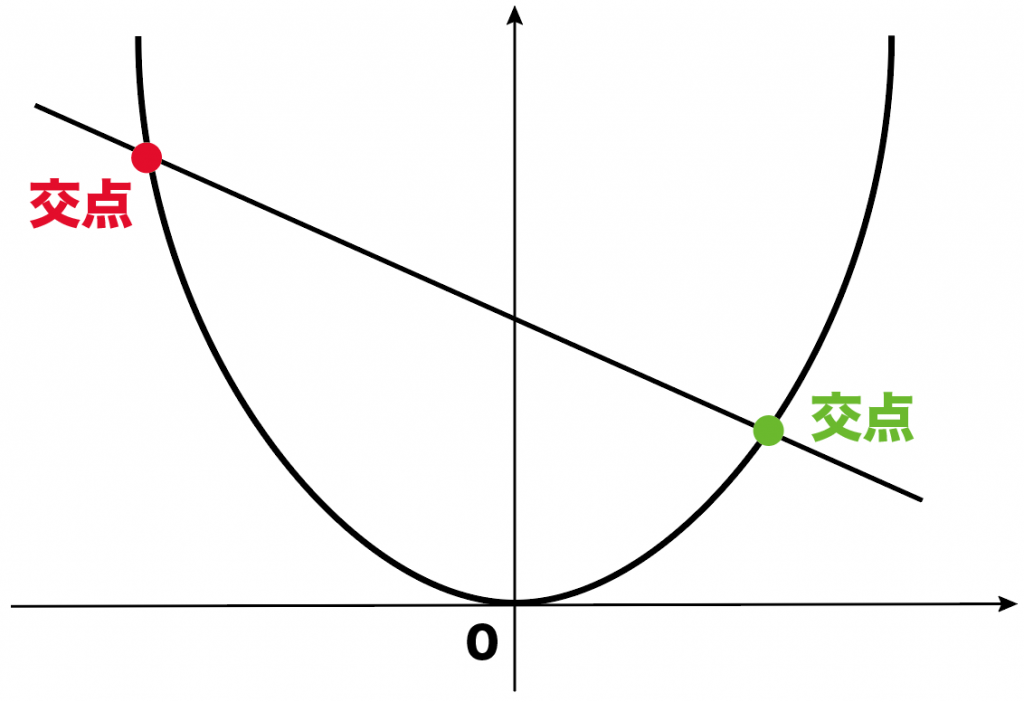
やり方さえ知っておけば怖くない。
こんな問題が出てきたときに、
一緒に考えていこう!
うす!

年齢不詳の先生。教育大学を卒業してボランティアで教えることがしばしば。


























y=x²,y=ax²
(0<x<1)のグラフがあり、点(3,0)を通りy軸に平行な直線とその交点をそれぞれA,Bとする。
線分の長さが6のとき
㈠aの値は? A. a=1/3
㈡直線ABの式? A. x=3
㈢三角形OABの面積? A. 9
㈠~㈢の答えがなぜそうなるのか分かりません。 答えの解説をお願いします。!
>y=x²,y=ax²
(0<x<1)のグラフがあり、点(3,0)を通りy軸に平行な直線とその交点をそれぞれA,Bとする。
線分の長さが6のとき
Bの座標をaで表してみよう。
y=ax2にx=3を代入すればBのy座標が計算できるはずだからね。
Bのy座標が出たらAのy座標からひくと、ABの長さ6になるっていうaに関する方程式を作れそうだね
aが出てちまえば後の問題も楽勝さ
yがxの2乗に、比例し、xの値が2~3まで増加するとき、変化の割合が3となる関数の式を求めなさい。
答えがy=二分の一x2 になるか分かりません。
教えてください。
>yがxの2乗に、比例し、xの値が2~3まで増加するとき、変化の割合が3となる関数の式を求めなさい。
答えがy=二分の一x2 になるか分かりません。
この関数をy=ax2と置いてみよう。
xの値が2の時、xの値が3の時、それぞれyの値をaで表してみて
そこからyの増加量を計算したら最後に、yの増加量をxの増加量で割ったら変化の割合3になった、というaに関する方程式を作ればいいね
中3後期中間テストの問題なんですが、(1)グラフが原点を通る。(2)変化の割合が一定でない。(3)x<0の時、xが増加すると対応するyの値も増加する。(4)グラフがy軸について対称である。などの問に合ったものを「ア・・y=3x イ・・y=2x+1 ウ・・y=-3xの2乗 エ・・y=5x」の中から選べというものがありました。合ったものの見分け方がわかりません。覚え方等を教えていただきたいです。
>(1)グラフが原点を通る。(2)変化の割合が一定でない。(3)x<0の時、xが増加すると対応するyの値も増加する。(4)グラフがy軸について対称である。などの問に合ったものを「ア・・y=3x イ・・y=2x+1 ウ・・y=-3xの2乗 エ・・y=5x」の中から選べ
「変化の割合が一定でない」っていうヒントから、この関数は一次関数でもないし比例でもないってことがわかるね。
残るは二次関数か反比例。で、選択肢に反比例がないから二次関数が答えだ!
2次関数と1次関数の変化の割合はどこが違って、どうして違うのですか?
>2次関数と1次関数の変化の割合はどこが違って、どうして違うのですか?
変化の割合の意味は同じだよ。
xが1増えた時に、yがどれくらい増えたり減ったりするのかってこと。
一次関数の時はずっとこの変化の割合が同じだったけど、
二次関数だとこの変化の割合はうねうねと変化するよ。なぜなら、直線ではなく放物線だからね
関数y=axの2乗についてxの値が1から3まで増刊号するときの変化の割合が1次関数y=ax+1の変化の割合と等しくなった。aの値を求めよ。
>関数y=axの2乗についてxの値が1から3まで増刊号するときの変化の割合が1次関数y=ax+1の変化の割合と等しくなった。aの値を求めよ。
二次関数の変化の割合の求め方の公式を使うと便利。
それで求めた変化の割合が1次関数y=ax+1の変化の割合、つまり傾きのaと等しくなるというaに関する方程式を作ればいいよ〜
二次関数のグラフが曲線になることを証明して下さい!
一次関数と二次関数のグラフの違いとなぜそれがそのようなかたちになるのかお願いします。曲線とかです!