平行線と線分の比の問題の解き方がわかる3ステップ
こんにちは!ぺーたーだよ。
相似の単元では、
相似条件とか、
相似の証明とか、いろいろ勉強してきたね。
今日は ちょっと新しい、
平行線と線分の比のから辺の長さを求める問題
について解説していくよ。
たとえば、つぎのような問題ね↓
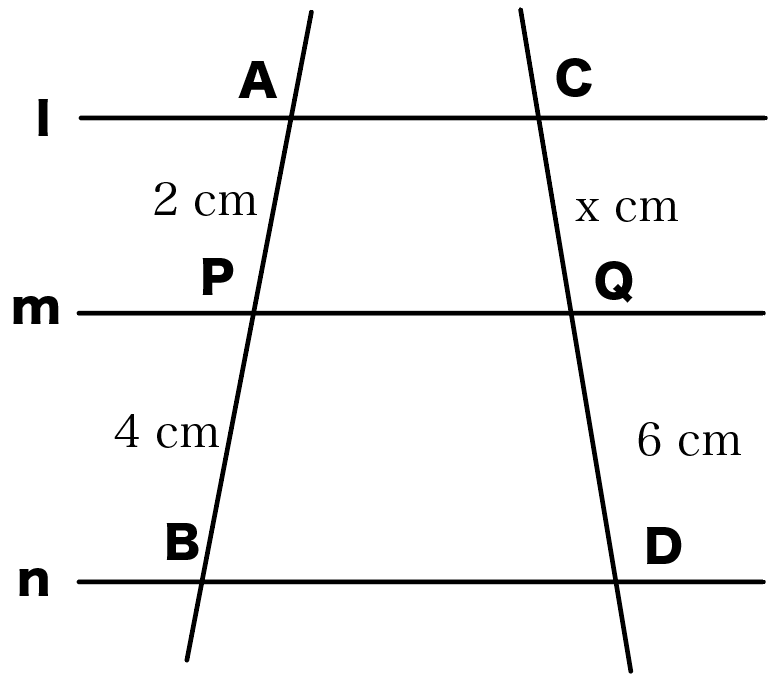
平行線とか線分がたくさんあって、ちょっと難しそうだね。
だけど、慣れちゃえば簡単。
「これはできるぜ!」っていうレベルになっておこう。
次の段階に分けて説明してくね。
目次
- 平行線と線分の比の性質
- 問題の解き方3ステップ
- 問題演習
平行線と線分の比の性質ってなんだっけ??
問題をとく前に、
平行線と線分の比の性質を思い出そう。
3つの平行な直線(l・m・n)
と
2つの直線が交わる場面をイメージしてね。

このとき、
AP:PB=CQ:QD
が成り立つんだ。
つまり、
平行線にはさまれた、
向かいあう線分の長さの比が等しい
ってわけね。
これさえおさえておけば大丈夫。
平行線と線分の比の問題もイチコロさ!
平行線と線分の比の問題の解き方3ステップ
さっそく、平行線と線分の比の問題を解いてみようか。

この手の問題は3ステップでとけちゃうよ。
- 対応する線分を見極める
- 比例式をつくる
- 比例式をとく
Step1. 対応する線分を見極める
平行線と線分の比がつかえる線分を見極めよう!
平行線にはさまれた線分のセット
をさがせばいいってわけね。
練習問題でいうと、
- AP
- PB
- CQ
- DQ
で平行線と線分の比がつかえそうだ。
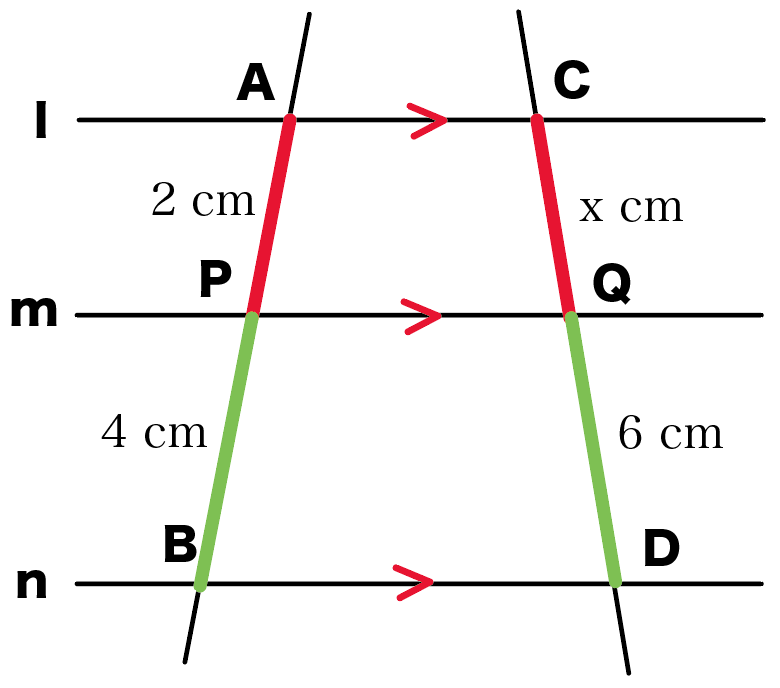
なぜなら、こいつらは、
3本の平行線(l・m・n)にはされまれてるからさ。
あきらかに3本の平行線に囲まれてる。
Step2. 比例式をつくる
平行線と線分の比の性質で比例式をつくってみよう。
平行線と線分の比の性質は、
2つの直線が、3つの平行な直線と交わるときAP:PB=CQ:QD
だったね??

だから、練習問題でいうと、
AP : PB = CQ : DQ
2 : 4 = x : 6
っていう比例式ができるはず!
Step3. 比例式をとく
つぎは、比例式をといてみよう。
練習問題でつくった比例式は、
2 : 4 = x : 6
だったよね??
比例式の解き方の「内項の積・外項の積」で解いてやると、
2 : 4 = x : 6
4x = 2×6
4x = 12
x = 3
になるね。
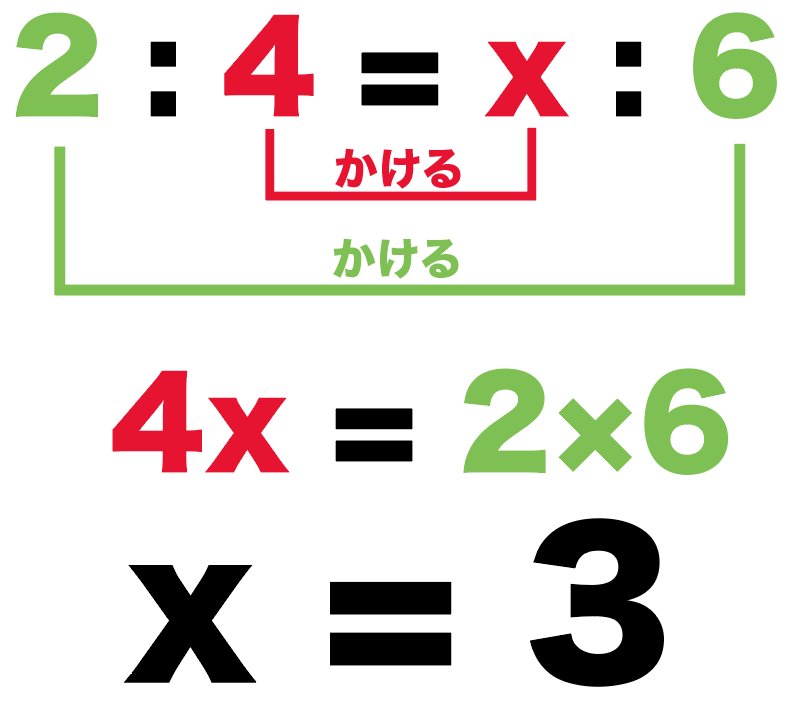
つまり、
求めたかったCQの長さは「3 cm」ってこと。
やったね!
平行線と線分の比に関する超実践的な2つの問題
平行線と線分の比の性質もだいたいわかったね。
あとは練習問題でなれてみよう。
今日はテストにでやすい問題を2つ用意したよ。
平行線と線分の比の問題になれてみようぜ。
平行線と線分の比の問題1.
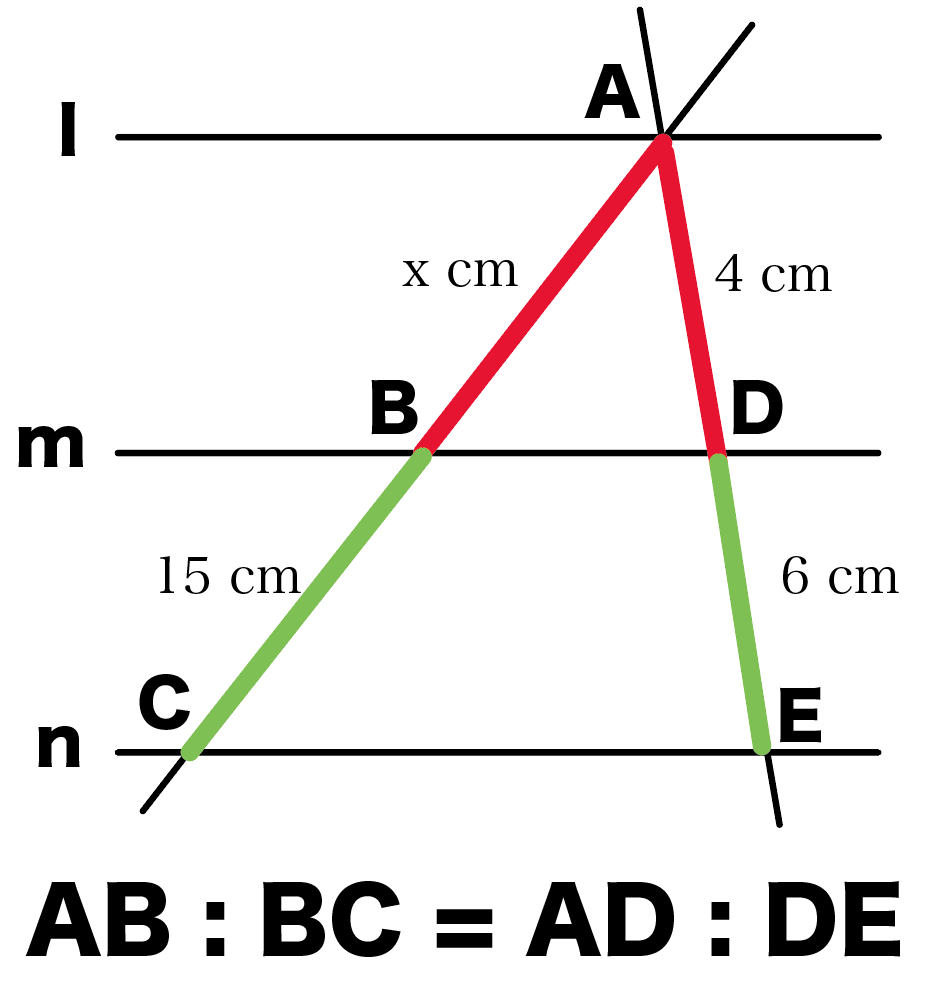
l//m// nのとき、xの大きさを求めなさい。
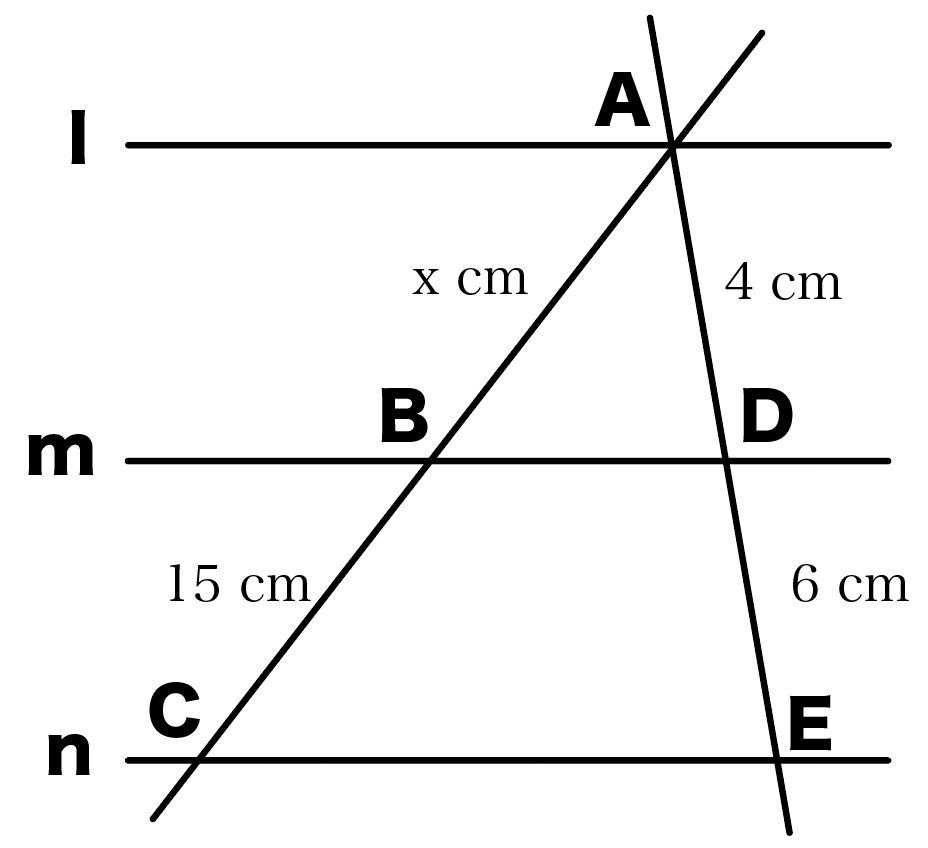
この手の問題は、
AB : BC = AD : DE
という平行線と線分の比をつかえば一発さ。
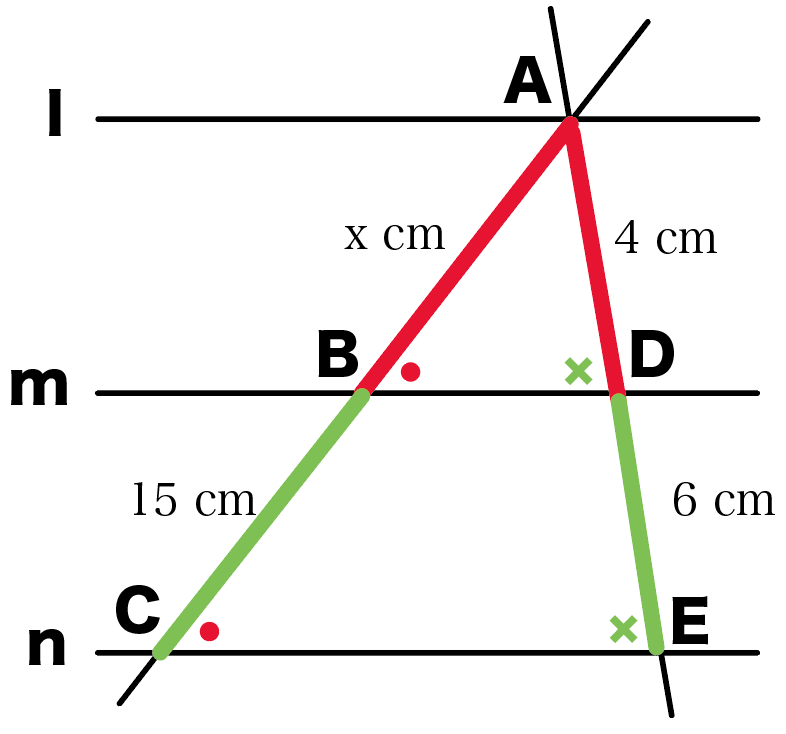
これは、△ABDと△ACEが相似だから、
対応する辺の比が等しいことをつかってるね。
えっ。
なんで相似なのかって??
それは、同位角が等しいから、
- 角ABD = 角ACE
- 角ADB = 角AEC
がいえるからなんだ。
三角形の相似条件の、
2組の角がそれぞれ等しい
がつかえるし。
さっそく、この比例式をといてやると、
AB : BC = AD : DE
x : 15 = 4 : 6
x = 10
になるね。
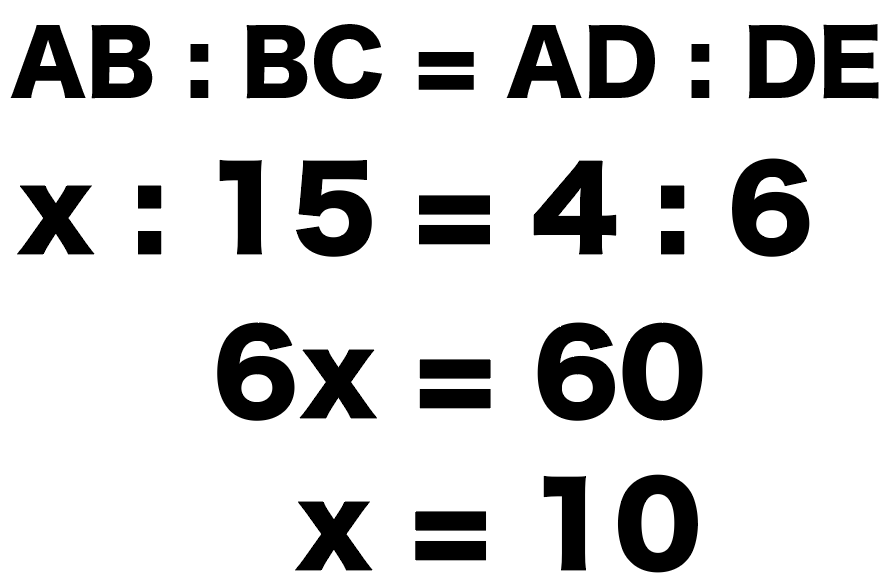
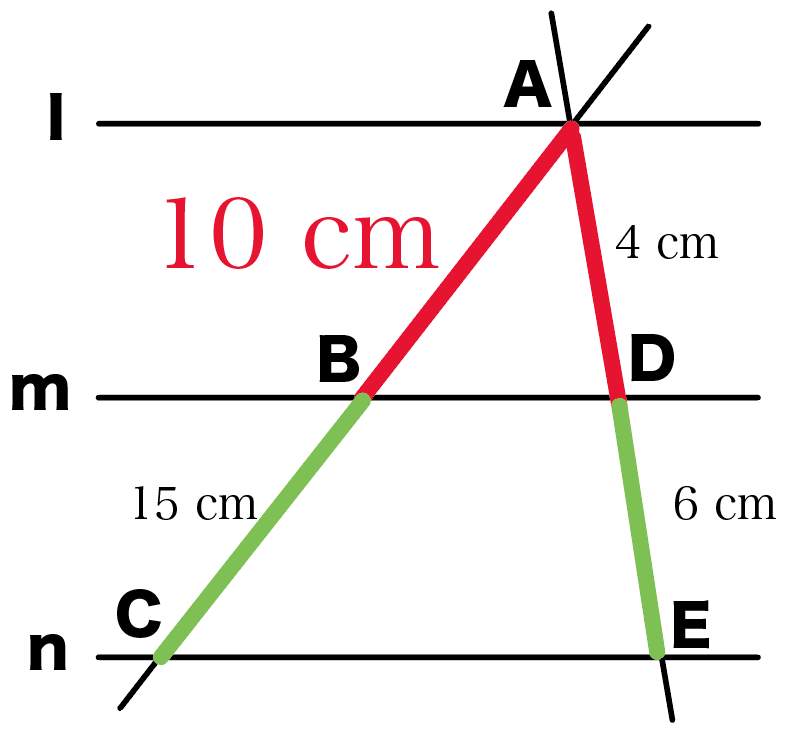
ってことは、ABの長さは、
10cm
になるってこと!
平行線と線分の比の問題2.
l//m// nのとき、xの大きさを求めなさい。
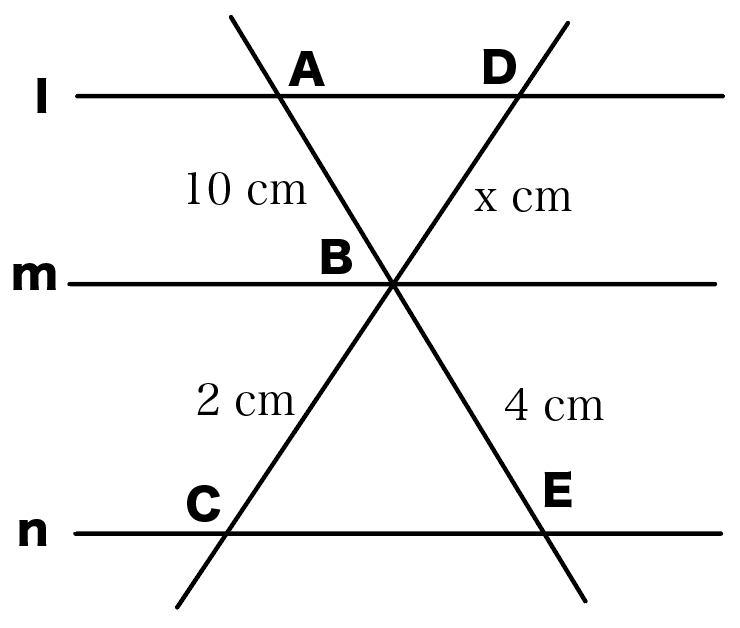
今度は直線がクロスしている問題だ。
対応する部分に色を付けるとこうなるよ。
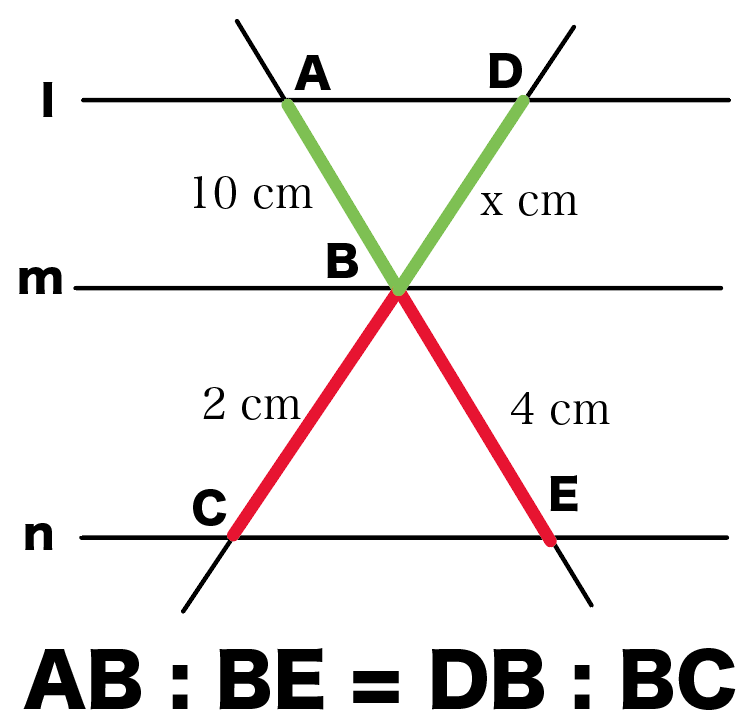
なぜなら、これもさっきと同じで、
△ABDと△EBCの相似をつかってるから使えるんだ。
l・m・nがぜーんぶ平行だから、
錯角が等しいことがつかえるね。
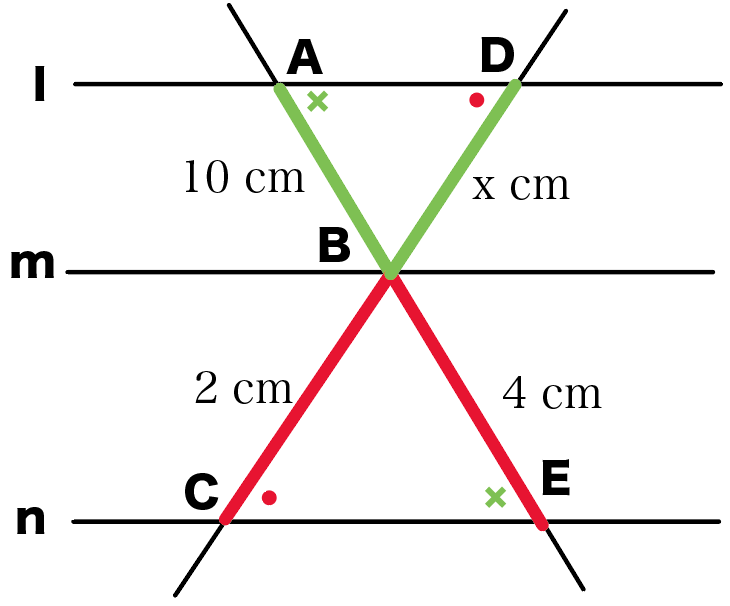
だから、
2組の角がそれぞれ等しい
っていう三角形の相似条件がつかえる。
比例式をといてやると、
AB : BE = DB : BC
10 : 4 = x : 2
4x = 20
x = 5
になるね。
まとめ:平行線と線分の比の問題は対応する辺をみつけろ!
平行線と線分の比の問題は、
対応する辺の比をいかにみつけるか
がポイント。
最後の最後に練習問題を1つ!
練習問題
l//m// nのとき、xの大きさを求めなさい。
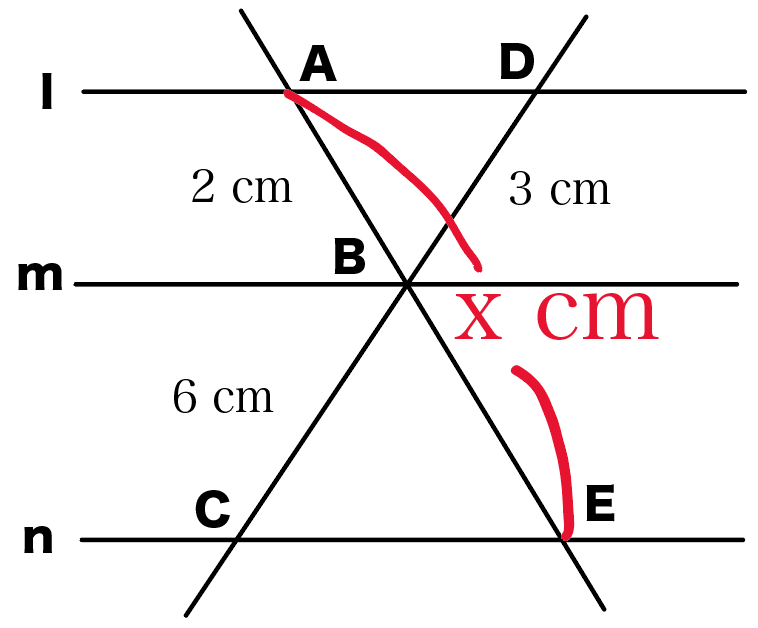
どう?とけたかな??
解答はここをみてみてね。
それじゃあ、また。
ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める

























初めまして。よろしくお願いします。
平行線で交わる2本の線なんですが、片方の線の全体が14センチ、その内のXを求めよという問題なんですが答えと合いません。
4:6=X:(14-X) この14-Xが56-4Xになって-4Xを6Xに足すようなんですが足す意味が理解できません。教えて下さい。お願いいたします。
質問ありがとう!
>4:6=X:(14-X)
これは比例式だね。
比例式の解き方では、
外項の積・内項の積を使っていくよ。
比の内側同士と、外側同士をかけたものが等しいっていう等式を作ればいいのさ
平行線と線分の比の性質について質問させてください!
この記事では、AP:PB=CQ:DQだけしか載ってませんが
他にも「AP:AB=CQ:CD」や「AP:CQ=PB:QD」などが
私の参考書には載ってました!
平行線と線分の比の性質は1つですか?3つですか??
AP:PB=CQ:DQが言えると、他の2つの「AP:AB=CQ:CD」や「AP:CQ=PB:QD」も導けるよ。
3つ覚えてもいいし、余裕がないときは1つ覚えて、他を導けるようにしておけばいいね!
み、導く(´・ω・`)?
長文になるかもしれません…
過去問の解説で、↓こんなのが出てきました!全く理解できませんでした…教えてください。
DB:BC=AB:AC
(図形は、[平行線と線分の比の問題1]同じ位置です。)
>過去問の解説で、↓こんなのが出てきました!全く理解できませんでした…教えてください。
DB:BC=AB:AC
(図形は、[平行線と線分の比の問題1]同じ位置です。)
錯角を使うと、
△ABCと△DCBが相似になるよ
平行線と線分の比の問題1.
の形の問題(l上で二直線が交点を持つ)で、
線分の比が等しいときにm,mが平行であることはわかるのですが、lも平行だということはできますか?
出来るなら、どうやっていえますか?
>平行線と線分の比の問題1.
の形の問題(l上で二直線が交点を持つ)で、
線分の比が等しいときにm,mが平行であることはわかるのですが、lも平行だということはできますか?
出来るなら、どうやっていえますか?
できるんじゃないかな。
三角形の相似を証明して、錯角か同位角が等しいことを使って言えそうだ
Ap:Ab=aq:ac とap:pb=aq:qcという式が私の参考書にあるのですがどの問題でどの式を使うのかわかりません
>Ap:Ab=aq:ac とap:pb=aq:qcという式が私の参考書にあるのですがどの問題でどの式を使うのかわかりません
どういう図なのか次第かな!
ちょっとわからなくてごめんよ
図形において、補助線を引く場合、
平行な補助線を引くのか、対角線に引くのかの
見分け方はありますかね?
>図形において、補助線を引く場合、
平行な補助線を引くのか、対角線に引くのかの
見分け方はありますかね?
場合によるかな!
どの公式か?どの図形の性質を使うのか?によって使い分けよう
とても分かりやすいです!
ありがとう!
平行四辺形ABCDにおいて、辺CD 辺DAの中点をそれぞれM.Nとし、線分AMとBMの交点をPとするとき AP:PM NP:PBの比を求めよ 解き方と答えお願いします!
>平行四辺形ABCDにおいて、辺CD 辺DAの中点をそれぞれM.Nとし、線分AMとBMの交点をPとするとき AP:PM NP:PBの比を求めよ 解き方と答えお願いします!
AMとBMが交わらない!汗
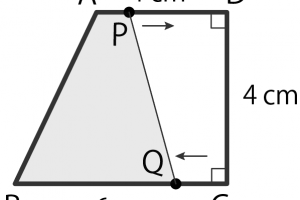
台形の対角線の交点をとおる平行線の長さがわかりません
上辺が6センチ、下辺が9センチです
解説お願いします
どこに平行なのかにもよるな!