確率のコツを知りたい!!
こんにちは!この記事をかいているKenだよ。ビビン丼は間違いないね。
中学数学の確率はぶっちゃけ、ムズい。
樹形図かかなきゃいけないし、
サイコロふらなきゃいけないし。
もう、つかれちゃうよね。
だけど、確率はテストで狙われやすい単元だ。
逃げるわけにはいかないね。
今日は、そんな確率の問題を倒すために、
確率を攻略できる5つのコツ
を伝授するよ。
中学数学でつかえる!確率の問題の5つのコツ
確率のコツは5つあるよ。
- 問題のパターンに慣れる
- 「少なくとも」は近道
- 樹形図を徹底マスター
- 同じものでも区別
- 確率の範囲は0~1だよ
コツ1. 問題パターンに慣れる
問題のパターンに慣れよう。
いろんな種類があるからね。
問題の種類ごとにつかえる公式だったり、
確率の求め方がちがう。
パターンを知っておくだけで楽になるよ。

たとえば、
などなど。
いろんなタイプの問題をといてみよう。
できなかった問題の解き方をつぶしていくのがコツだよ。
コツ2. 樹形図を徹底マスター
中学数学の確率では、
が重要なんだ。
なぜなら、
場合の数を調べるときに樹形図をつかうからだ。
確率の求め方は、
(あるできごとの場合の数)÷(すべての場合の数)
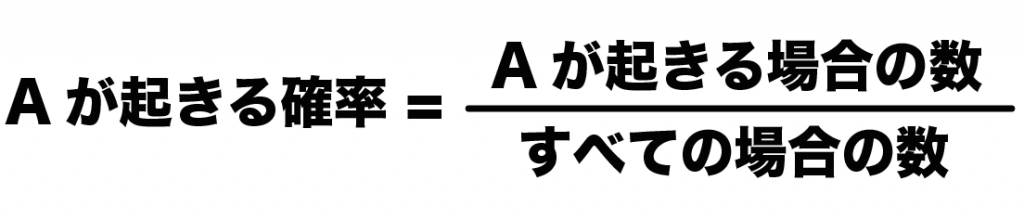
だったよね??
場合の数がわからないと確率が計算できないってわけ。
つまり、「樹形図」をマスターしていないと確率が計算できないんだ。
樹形図の書き方はおぼえておこう!
>>詳しくは「樹形図の書き方」をみてね。
コツ3. 「少なくとも」は近道をつかえ!
問題文に「少なくとも」がついてたら注意。
「少なくとも」がついている問題の解き方をつかってみよう!
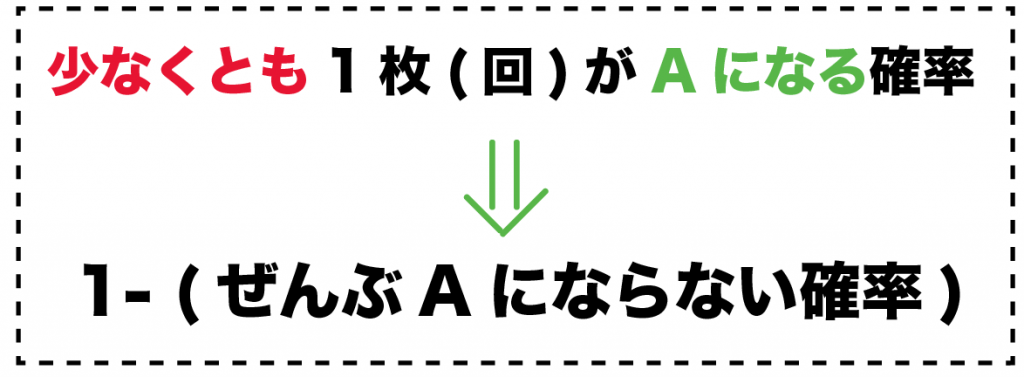
少なくとも1枚(回)がAになる確率
だったら、
1 – (ぜんぶAにならない確率)
を計算すればいいんだ。
えっ、なぜこんなメンドイ計算をするのかって!?
じつはその理由は、
場合の数が少なくて数えやすいからなんだ。
だから、確率の計算もしやすい。
詳しくは「少なくともがつく確率の解き方」の記事をよんでみね。
コツ4. 同じものでも区別する
確率の問題では、
同じにみえるものを区別すること
が重要だよ。
たとえば、サイコロを2つ投げる問題だったら、
- サイコロAの目
- サイコロBの目
と区別するよ。
そっくりな当たりくじ同士でも、
- 当たりくじ1
- 当たりくじ2
って別々ものものとしてみるよ。

こんな感じで、
見た目が同じものを区別していこう!
コツ5. 確率が0~1になってるか確認
計算した確率が、
0から1の間
におさまっているか確認しよう。
もし、計算できても、
確率が2とか、
300とか、
100000になってたら間違いだ。
なぜなら、
確率の範囲はゼッタイに「0から1」だからね。
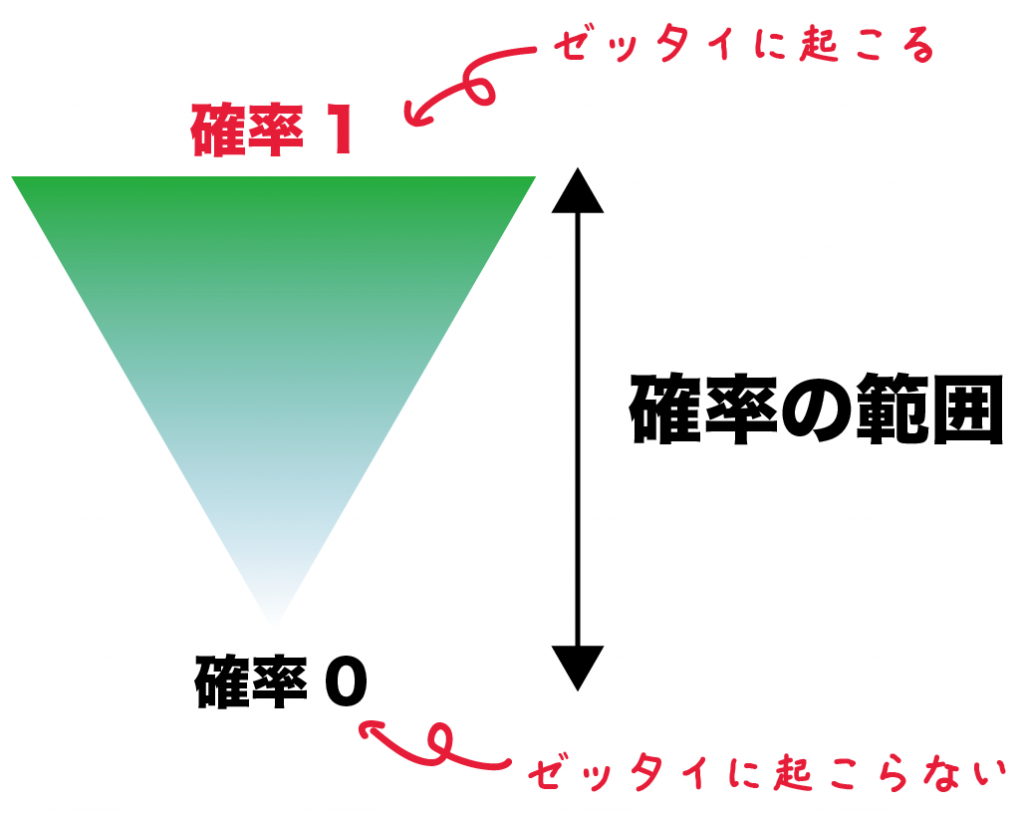
確率が1だと100%ゼッタイにおこる確率になるし、
0だとゼッタイに起きない確率になる。
計算後にチェックしてみよう^^
まとめ:確率の問題のコツをおさえてクリア!
確率の問題は特殊。
方程式をといたり、
関数の交点を求めたりするのとは訳がちがう。
シンプルだけどむずい単元だ。
コツをおさえて問題になれていこう!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。
























点Pが動く問題の解き方とコツを簡単にわかりやすく教えてください。あと水槽の問題も教えてください。
>点Pが動く問題の解き方とコツを簡単にわかりやすく教えてください。
「動点の問題の解き方がわかる3ステップ」を読んでみて!
>あと水槽の問題も教えてください。
問題送ってみて!
机に向かう(勉強する)までに時間がかかります。環境を変える以外に何か解決策はありますか?
>机に向かう(勉強する)までに時間がかかります。環境を変える以外に何か解決策はありますか?
机しかないところに行こう笑
図書館とかね
1次関数の応用問題が苦手です。
基本はできるのですが…
コツがあれば教えてください。
>1次関数の応用問題が苦手です。
基本はできるのですが…
コツがあれば教えてください。
やってることはxとyの文字で表す文字式の問題だよね。
あとは、いくつか出やすいパターンがあるからその問題の種類をマスターしておけばいいかな。
たとえば、動点の問題とかね。
サイコロを2回振って
最初に3,二回目に3
が出る確率は、36分の1?
>サイコロを2回振って
最初に3,二回目に3
が出る確率は、36分の1?
そうだね!
カードを続けて2枚ひいて
和が何の数で……………
っていう問題は p c どっちでときますか?
>カードを続けて2枚ひいて
和が何の数で……………
っていう問題は p c どっちでときますか?
Cだね!
2 5 が書かれているカードが1枚ずつあります。
もう2枚白紙のカードがあり、そこには、2回さいころをふって、出た数をそれぞれかきます。
この4枚(1つずつ数が書かれています)をならべてできる最も小さい数をmとする時、10の位にくる数字はどれが1番確率高いですか
5らしいですが、理由がわかんないです
大小2つのサイコロを同時になげ、出た目の数をX座標、小さいさいころの出た目の数をy座標とする。例えば、大きいサイコロの目が5、小さい目が2の場合、このようにとった点が傾き1、切片2の線上の点である確率を求めよ
>大小2つのサイコロを同時になげ、出た目の数をX座標、小さいさいころの出た目の数をy座標とする。例えば、大きいサイコロの目が5、小さい目が2の場合、このようにとった点が傾き1、切片2の線上の点である確率を求めよ
サイコロ2つの確率は表に書いて場合の数を数えてみよう!
長方形が縦3個✖︎横3個並んである(長方形が全部で9個)、左下の端A地点から右上の端B地点までの最短距離で行く道順は何通りあるか?
解き方教えてください
A地点からB地点まで最短距離で行く道順は何通りあるか?
縦3個、横3個並んであり(全部で9個)、左下の端A地点から右上の端B地点まで。
1,1,1,2,2,3,の数字が書かれたカードが1枚ずつあり,同時に2枚引いたとき,選んだカードに書かれた数字の差が1である確率を求めなさい。 という問題が分かりません。答えが3/15らしいんですが…
サイコロを600回投げたとき5の目がでる回数は必ず100回になる。
というのはなぜ正しくないと言えるのでしょうか。
>1,1,1,2,2,3,の数字が書かれたカードが1枚ずつあり,同時に2枚引いたとき,選んだカードに書かれた数字の差が1である確率を求めなさい
差が1になる場合は
2-1
3-2
の2通りあよね。それぞれの確率を計算して足せばいいよ
>サイコロを600回投げたとき5の目がでる回数は必ず100回になる。
というのはなぜ正しくないと言えるのでしょうか。
やってみればわかるけど、実際には確率通りにはいかない。
試行回数が多ければ多いほど確率通りの結果が得られるけど、絶対にそうなるとは言えないね。
期待値と実際の試行結果は異なる
「袋の中に、赤色、白色、黄色、青色の球が1個ずつ入っています。この袋の中から球を1個ずつ4回続けて取り出し、取り出した順に横一列に並べます。このとき、赤色の球と白色の球がとなりあって並ぶ確率を求めなさい。」
という問題があるのですが、これは樹形図で解く事は可能ですか?
答えは1/2となっているのですが…絶対1/3になってしまうので、樹形図の書き方が悪いのでしょうか?
>袋の中に、赤色、白色、黄色、青色の球が1個ずつ入っています。この袋の中から球を1個ずつ4回続けて取り出し、取り出した順に横一列に並べます。このとき、赤色の球と白色の球がとなりあって並ぶ確率を求めなさい。
「赤と白」を1つの「赤白」っていう玉だとみなして場合の数を数えるといいかも。
その場合の数を出せたら、「白赤」の場合も同じはずだからそれを2倍すれば良さそうだ
確率の問題が分からないと思いこれを見て、納得できるのですが塾のテキストをやると何故か出来ません。いつもそうなのですが、私はどうすればいいでしょうか?アドバイスお願いします。
>確率の問題が分からないと思いこれを見て、納得できるのですが塾のテキストをやると何故か出来ません。いつもそうなのですが、私はどうすればいいでしょうか?アドバイスお願いします。
実践が足りないのかも!
もっと問題をたくさん解いてみよう。間違えた問題の復習は忘れずにね
大小2つのサイコロを同時に投げる。
大きいサイコロの目をa、小さいサイコロの目をbとした時に
点(a,b)が、y=1/2x上にある確率を求めなさい。
解き方を教えてください!!
>大小2つのサイコロを同時に投げる。
大きいサイコロの目をa、小さいサイコロの目をbとした時に
点(a,b)が、y=1/2x上にある確率を求めなさい。
サイコロ2つの場合は表を書いて場合の数をカウントしていくといいよ。
確率の問題で、aさんbさんcさんdさんから二人組を作るときにaさんbさんになる確率をもとめなさい。という時に(a.b)と(b.a)は一つに数えていいのでしょうか?それともダメですか?
>確率の問題で、aさんbさんcさんdさんから二人組を作るときにaさんbさんになる確率をもとめなさい。という時に(a.b)と(b.a)は一つに数えていいのでしょうか?それともダメですか?
組み合わせの問題だね。
1つに考えていいよ!
ab二つのサイコロを同時に投げ、出た目の数をそれぞれabとするとき
2a+b≥15となる確率を求めよ
という問題が分かりません!
教えてください(´;ω;`)
>ab二つのサイコロを同時に投げ、出た目の数をそれぞれabとするとき
2a+b≥15となる確率を求めよ
サイコロ2つのパターンは表を書いて場合の数を地道に数えるといいよ〜
AさんとBさんが階段の途中の同じ段に立っています。2人でじゃんけんをし、勝てば3段上り、あいこなら二人とも1段ずつ上がれて、負けたら1段降りるゲームをしました。2回じゃんけんをしたとき2人の段の差が4段になる確率を求めなさい。
この問題の答えは9/4になるらしいのですが全然その答えになりません。どうやって解けばいいのでしょうか?来年受験なので教えてもらいたいです。
>AさんとBさんが階段の途中の同じ段に立っています。2人でじゃんけんをし、勝てば3段上り、あいこなら二人とも1段ずつ上がれて、負けたら1段降りるゲームをしました。2回じゃんけんをしたとき2人の段の差が4段になる確率を求めなさい。
このゲームでは1回勝ち負けが発生すると差が四段になるから、求める確率は、
勝って引き分ける
という場合の時のものだ。AとBが勝つ2パターンの場合の数を計算してみよう
1 2 3 4 5のカードがあり2枚取り出して2桁の整数をつくるとき整数は何とうり
かちゅもんだい
>1 2 3 4 5のカードがあり2枚取り出して2桁の整数をつくるとき整数は何とうり
かちゅもんだい
樹形図書いてみようぜ
さいころを2回投げるとき、最初に出る目が2
回目に出る目より小さい確率はどう求めればいいですか?
>さいころを2回投げるとき、最初に出る目が2
回目に出る目より小さい確率はどう求めればいいですか?
サイコロ2個の問題は表をかいて場合の数をカウントすると分かり易いよ〜
樹形図を書くときのコツはありますか?
もしあれば教えて下さい。
樹形図の書き方を読んでみて!
白玉2個赤玉3個青玉1個が入った箱がある。この箱から玉を同時に2個取り出すとき、同じ色の玉を取り出す確率を求めなさい。
という問題が分かりません。教えてください!!
玉の確率の問題の解き方を読んでみて!
樹形図はたくさんの数が出たとき全て書くのですか⁇⁇
全ての枝を書く必要はないよ!
省略して場合の数をカウントするのもあり
男子4人と女子2人の中から、くじで図書委員を2人決めるとき、男子と女子が1人ずつ選ばれる確率は15分の8らしいんですけど、何故ですか?また、「1人ずつ」や「赤玉と白玉を1個ずつ」などの問題はどうやって解けばいいですか?
サイコロを3つ振るとき、樹形図が書くのが大変です。どうやったら簡単に調べられるでしょうか?
明後日(5月14日)がテストです。申し訳ありませんが、早めの回答お願いします…。
クラブ活動、3日練習したら1日休み、1週目の月から始める場合、1回目の休みは木曜日となる。次の問いに答えなさい。
1 10回目の休みの日は、何曜日か 答え:金曜日、式不明
2 10周目の木曜日は、何回目の練習日か 答え:51回目、式不明
3 200回目の練習日は、何週目の何曜日か 答え:式不明