くじ引きの確率の問題の公式ってあるの??
こんにちは!この記事をかいているKenだよ。オレンジは目覚めにいいね。
中学数学の確率でたまーに、
くじ引きの問題
ってあるよね??
たとえば、
6本のうち当たりくじが4本あるとき、当たりくじをひく確率を求めなさい。
っていう感じで。

こういう問題はむずかしそう。
だけど、公式をつかえば5秒で確率を計算できるんだ。
くじ引きの確率を5秒で計算できる公式
つぎの公式で計算できるよ。
(当たりor はずれを引く確率)
=(当たりorはずれの本数)÷(残りのくじ本数)
あ、くじを1回引く場合だけどね。

たとえば、6本のうち2本が当たりくじだとする。
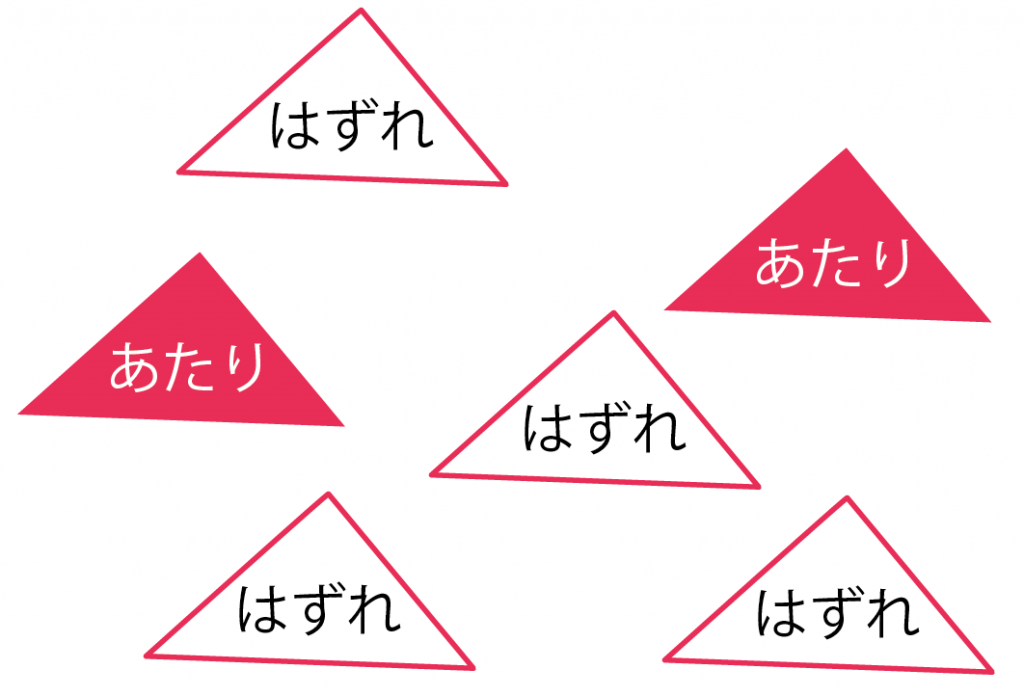
くじを1回ひいて「当たりくじ」がでる確率を求めてみよう。
- 当たりくじ: 2本
- ぜんぶのくじ数:6本
だよね。
公式をつかってやると、
(当たりくじを引く確率)
=(当たりくじの本数)÷(ぜんぶのくじ数)
= 2 ÷ 6
= 3分の1
になるんだ。
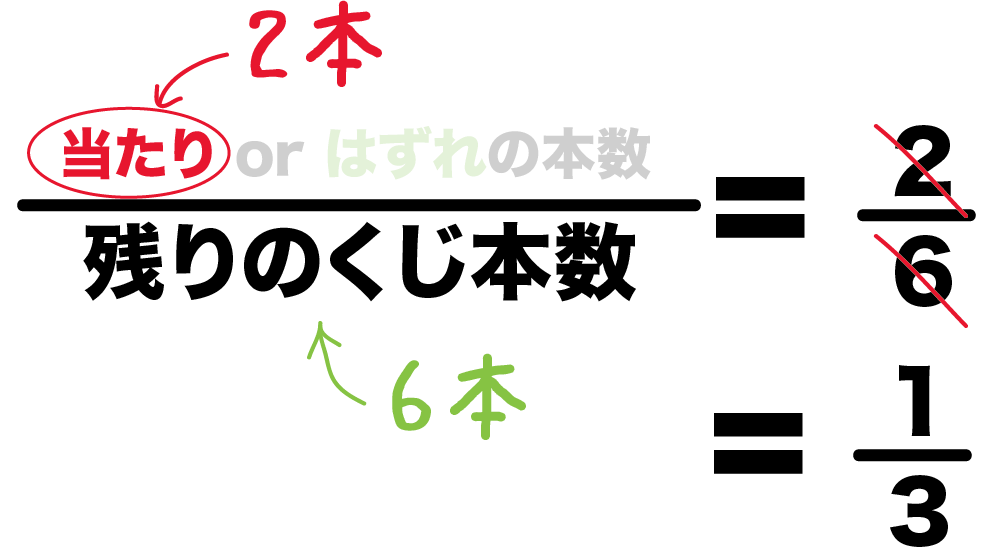
「当たりくじの数」を「残りのくじ数」でわるだけ。
簡単でしょ!?
なぜ、くじ引きの確率が公式が使えるんだろう!?
でもさ、なんで公式が使えるんだろう??
ちょっと怪しいよね。。
この公式がつかえる理由は、
1つ1つのくじ引きを区別しているから
なんだ。
「当たりくじ」たちはすごく似ている。
ぶっちゃけ、どれも同じ。
だけど、確率を計算するときは同じじゃだめなんだ。
こいつらを区別しないといけない。
たとえば、
- あたりくじ、その1
- あたりくじ、その2
みたいな感じでね。

当たりくじだけじゃなくて、はずれでも同じ。
見た目は同じだけど、別ものとしてあつかってやろう。
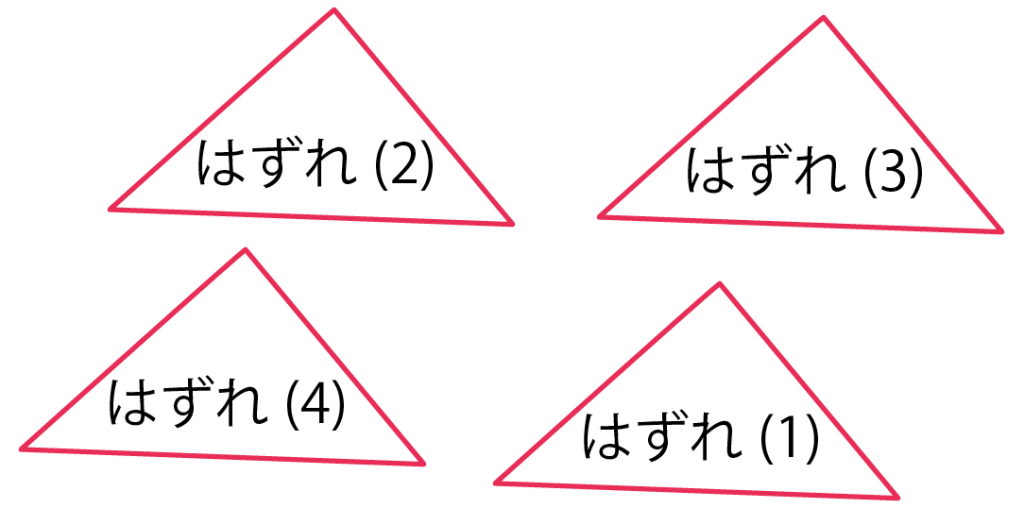
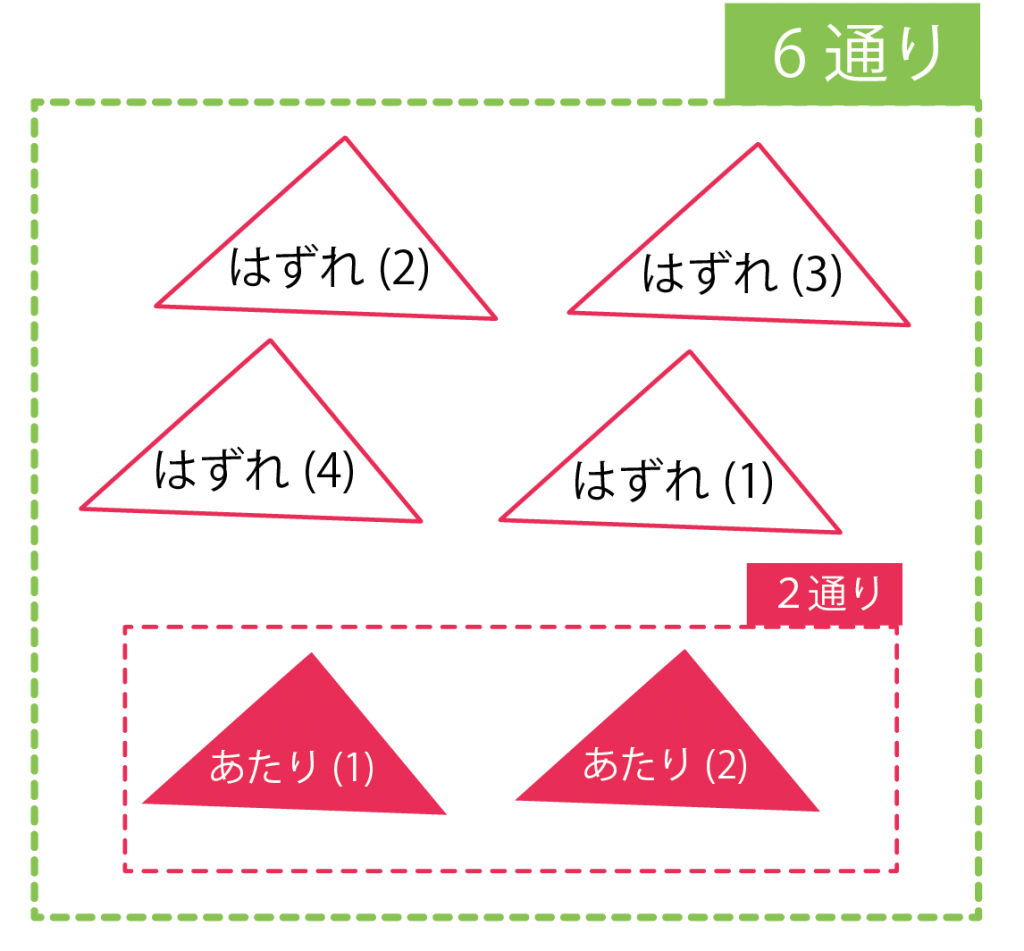
だから、「当たりくじのひき方」だったら、
- 当たりくじ(1)
- 当たりくじ(2)
の2通りがあるはず。
ぜんぶのくじ引きは、6通りのひきかたがある。
だから、確率の公式をつかってやれば、
(当たりくじの場合の数)÷(すべてのくじ引きの場合の数)
= 2÷6
=3分の1
になるんだ。
おめでとう!
くじ引きの確率もマスターだね^^
まとめ:くじ引きの確率の問題は公式で1発!
くじ引きの確率の問題??
おそれることはない。
ただ、公式で計算すればいいんだ。
くじの1つ1つが区別されるっておぼえておこう^^
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。

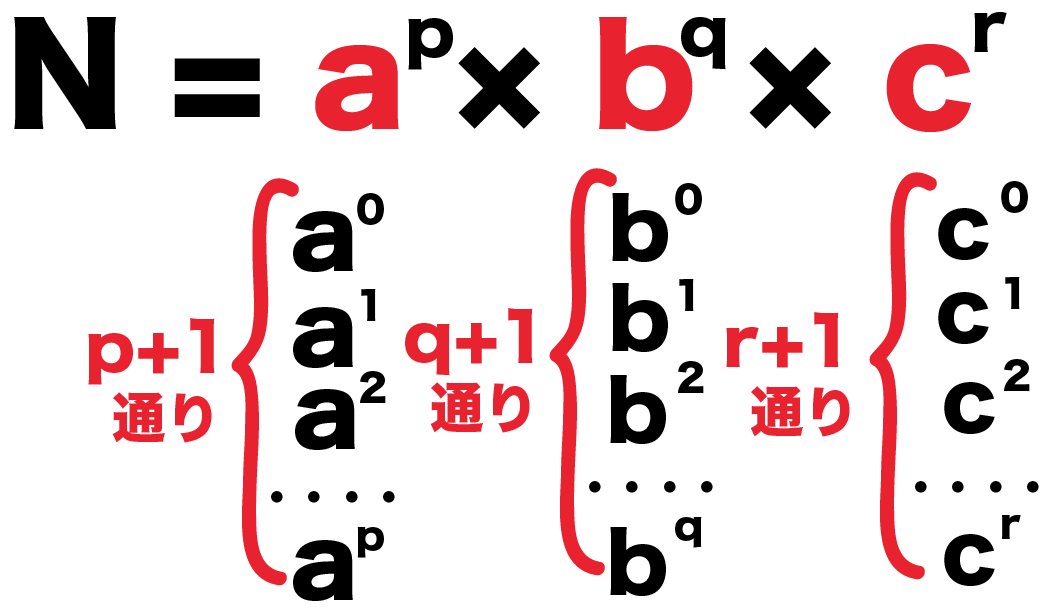
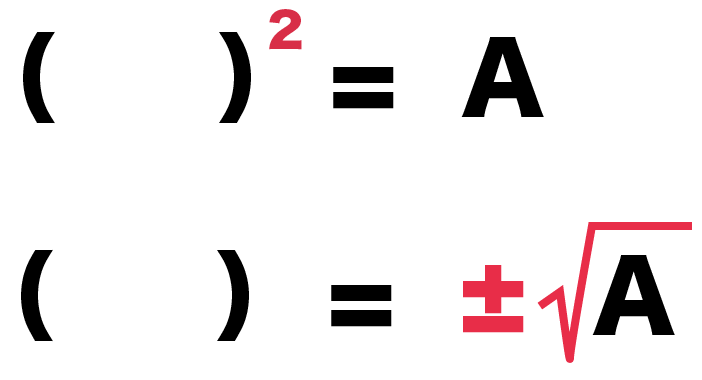
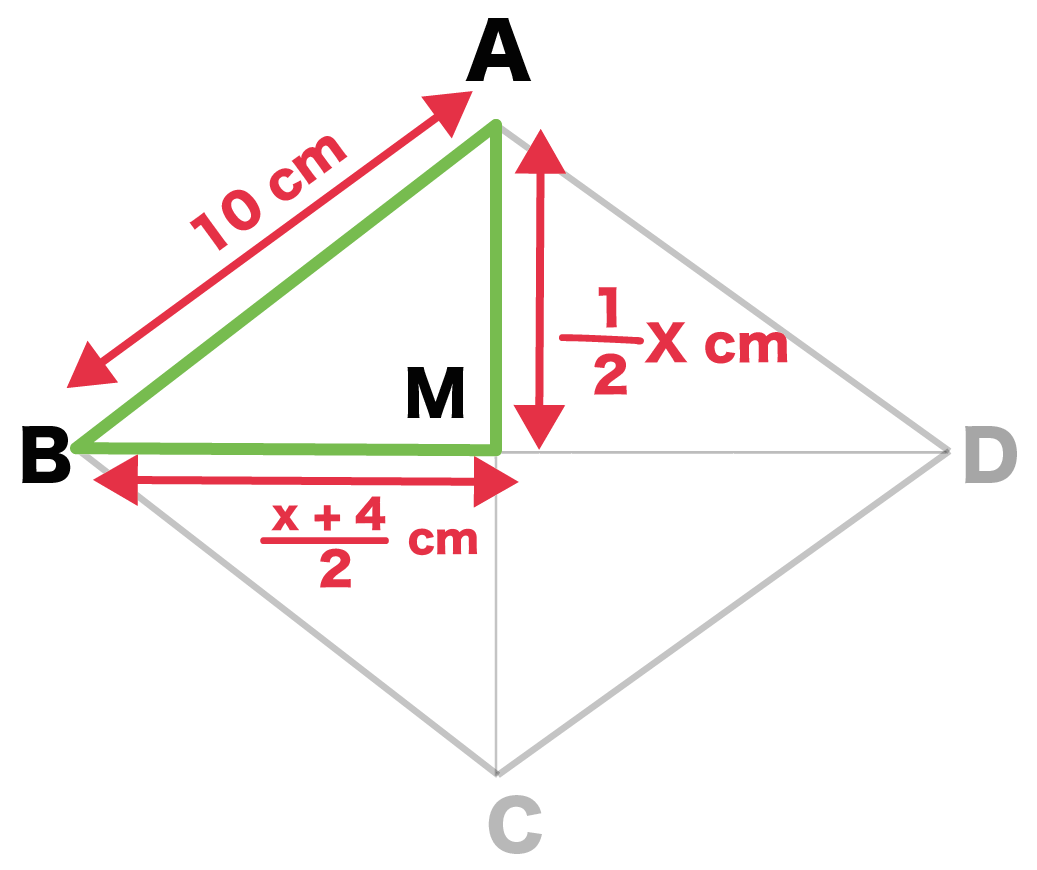



確率の問題でなぜ相対度数が関わっているのかが分かりません。教科書に載っていました。よろしくお願いいたします。
>確率の問題でなぜ相対度数が関わっているのかが分かりません。教科書に載っていました。よろしくお願いいたします。
やってることは同じだからね。
相対度数では、度数の合計のうち、ある特定の階級に当てはまる度数がどのくらいの割合かを表したもの。
確率はある場合の数が、全ての場合の数のうちどれくらいの割合かを表したものだ
生徒ABCDの5人の中から、くじ引きで3人発表者を決めます。次の確率を求めなさい。
①決まった3人の中にAが含まれる確率
②決まった3人の中にAとBが含まれる確率
これって公式が使えそうにないんですが、
この問題はどのような考え方で解けばいいんですか?
>生徒ABCDの5人の中から、くじ引きで3人発表者を決めます。次の確率を求めなさい。
①決まった3人の中にAが含まれる確率
Aが決まったものとして残り2人の場合の数を数えてみよう。
>②決まった3人の中にAとBが含まれる確率
これも同じでAとBが固定されて残りの1人の場合の数を数えてみよう!
Aの箱に1〜4までの数字のカード、Bの箱に3〜6の数字のカードが入っている。
同時にAからBへ、BからAの箱へ1枚ずつ引いたカードを移動させる。その後、Aの箱から1枚引いた時、3の倍数が出る確率をもとめなさい。
上の問いに対して…
AからBの箱へ移動させる時は、1枚なので確率は4分の1 ?その時、3のカードが出てしまう確率を出すのか?それ以外にのカードの確率をだせば良いのか分かりません。
同じようにBからAは4分の1?3の倍数は3と6があるから4分の2?
何から何をしたら良いかわからなくなってしまいました。教えてください。