2回以上くじを引いて「当たりくじ」がでる確率の計算方法

2回以上くじを引いたらくじ引きの確率は？？

こんにちは！この記事をかいているKenだよ。グレープフルーツは常備だね。

当たりくじをひく確率って、

（当たりくじの本数 ）÷（残りの本数）

だったよね？？

たとえば、5本中1本当たりのくじがあったとしよう。

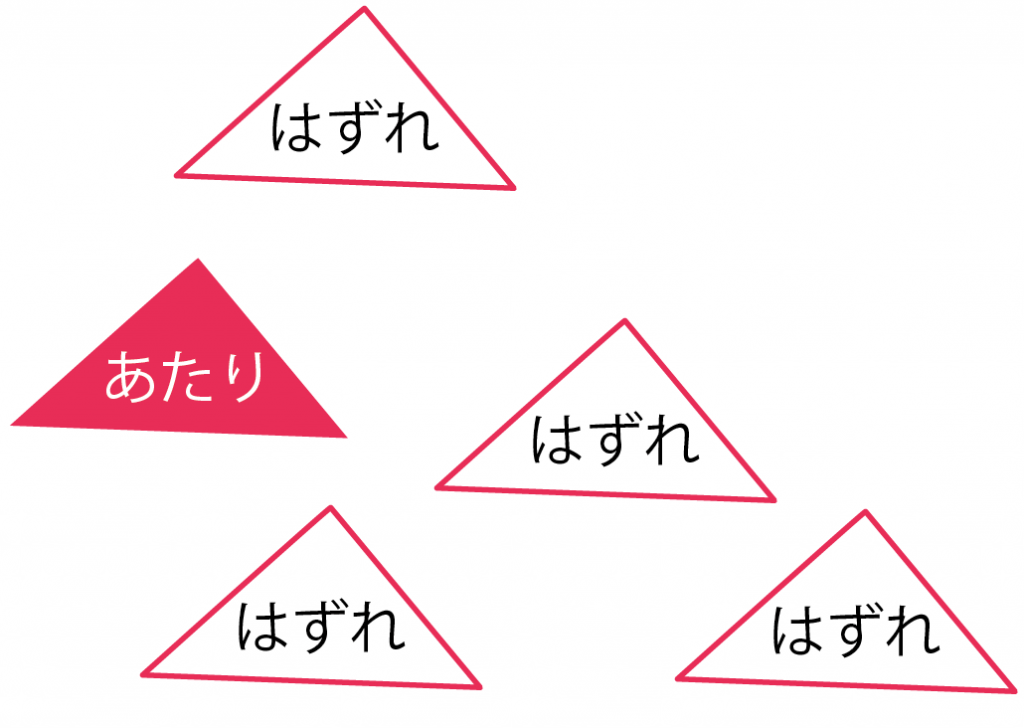
当たりくじがでる確率は、

（当たりくじの本数：1）÷（残りのくじ本数：5）
= 5分の1

になるんだ。

だけどさ、

この公式って、

くじを1回しか引かない問題でしか使えないよね？？

これじゃあ、2回以上ひく問題はとけないね！

そこで今日は、

2回以上くじを引くときの確率の求め方を解説していくよ。

よかったら参考にしてみて^^

2回以上くじを引くときの確率の求め方

確率の求め方はつぎの公式だよ。

（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）・・・

たとえば、「当たりくじを連続でひく確率」だったら、

（当たりくじの残り本数）÷（残りくじ本数）

をかけていけばいいね！

たとえば、つぎの例題をといてみよう。

例題

10本中3本が当たりくじのくじ引きがある。3回ひいて連続で当たりがでる確率を計算してください。

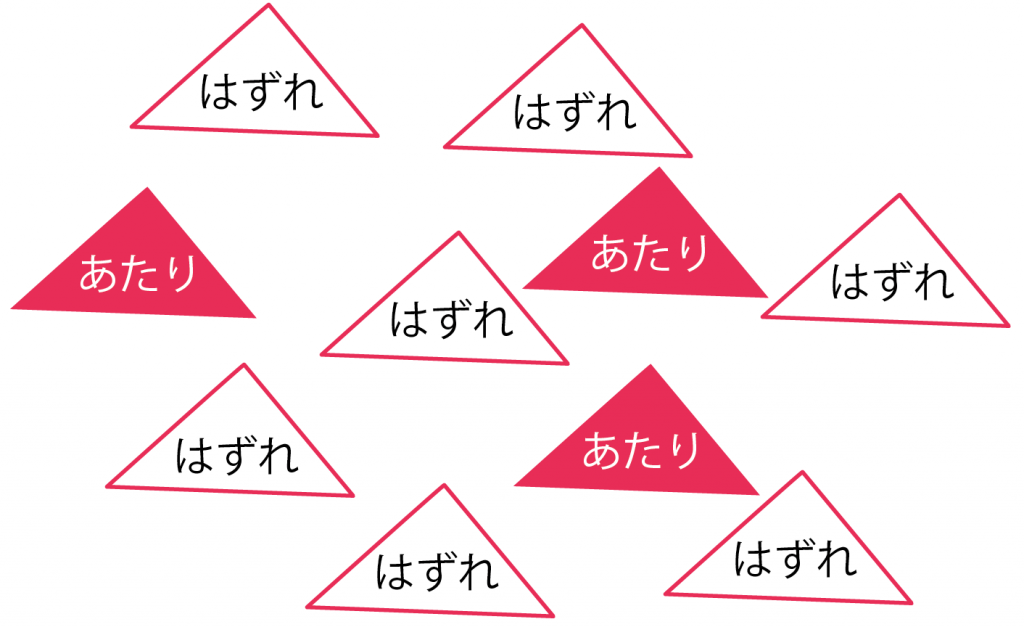
こいつは2ステップでとけちゃうんだ。

1. くじをひくごとの確率を計算
2. すべての確率をかける

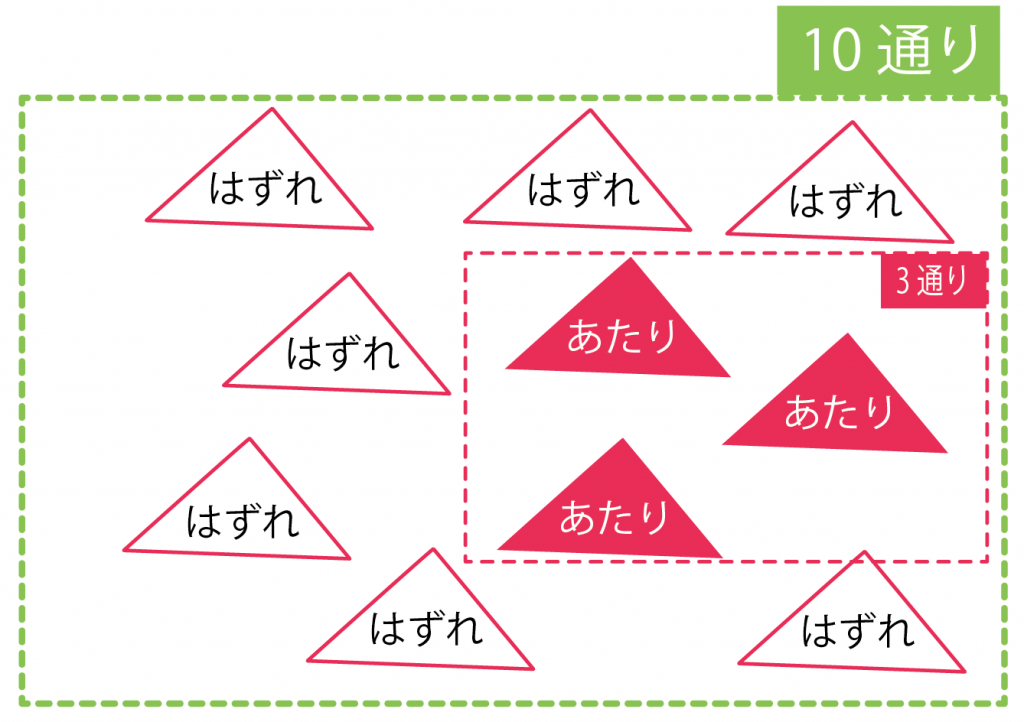
Step1. くじを引くごとの確率を計算

1回目は、

• 当たりくじ：3本
• 残りのくじ数：10本

のくじが箱にはいってるよね？？

だから、

当たりくじをひく確率は、

（当たりくじ数）÷（残りのくじ数）
= 3÷10
= 10分の3

になるよ！

2回目は、当たりくじを1本ひいたあとだ。

1本当たりくじが消えているはず。

だから、箱の中には、

• 当たりくじ：2本
• 残りの全くじ数：9本

が残ってるよね？？

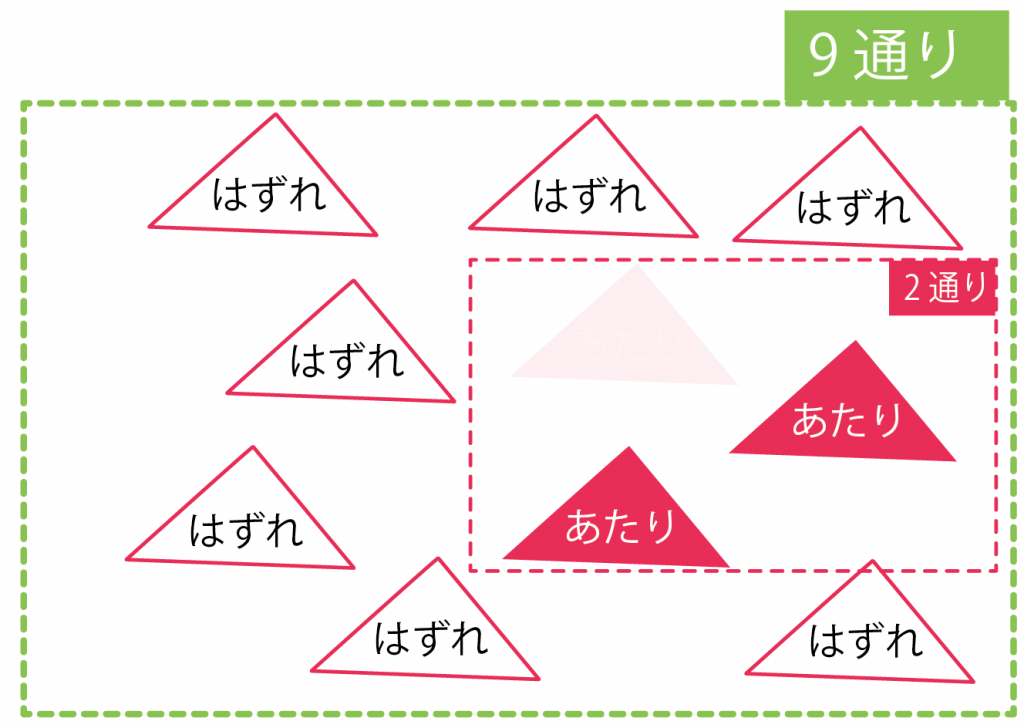
このとき、当たりくじをひく確率は、

（残当たりくじ数）÷（残りの全くじ数）
= 2÷9
= 9分の2

になるんだ。

おなじように考えると、3回めに当たりくじをひく確率は、

• 残当たりくじ数：1
• 残すべてのくじ数：8

が箱にのこっている。

だから、3回目に当たりをひく確率は、

（残当たりくじ数）÷（残すべてのくじ数）
= 1÷8
= 8分の1

になる。

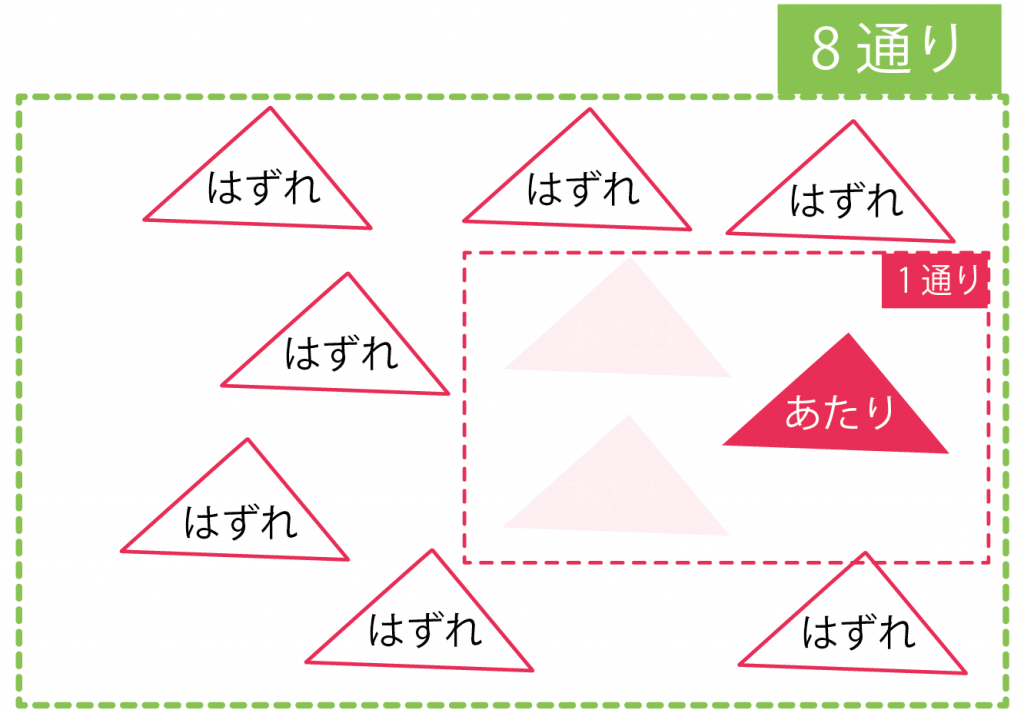
Step2. すべての確率をかける

あとは公式通りに、

（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）

を計算するだけ。

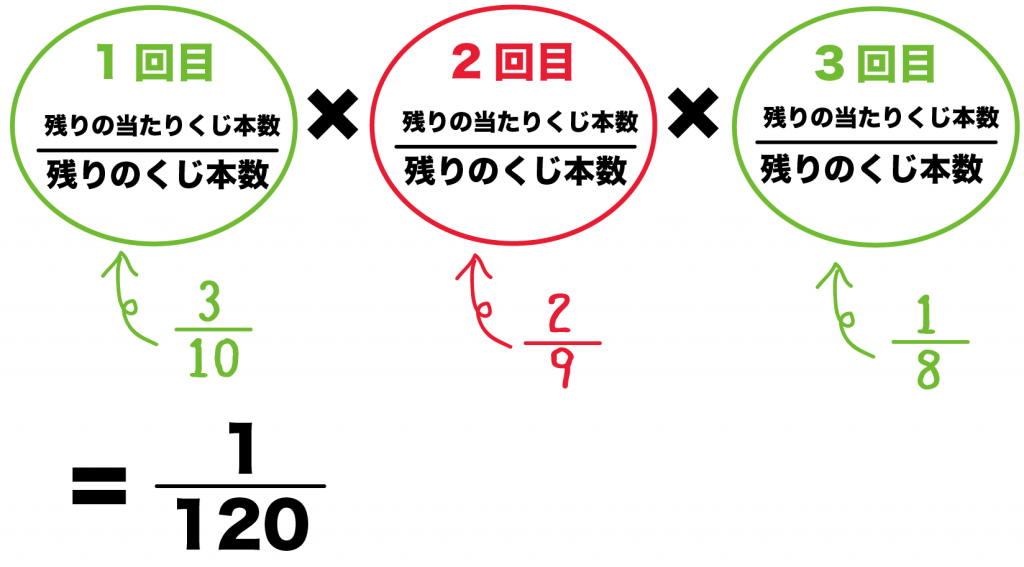
• 1回目の確率：10分の3
• 2回目の確率：9分の2
• 3回目の確率：8分の1

になったから、

（3回連続で当たりくじを引く確率）
=（1回目のくじ引きの確率）×（2回目のくじ引きの確率）×（3回目のくじ引きの確率）
= (10分の3)×（9分の2）×（8分の1）
= 120分の1

になるよ！

おめでとう！

これで2回以上くじを引く問題も攻略だね^^

まとめ：くじ引きの確率の問題は回数ごとにかける！

くじ引きの確率問題はどうだったかな？？

2回でも3回でもくじ引きをひいても大丈夫。

あとは公式になれていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。