円錐の体積の求め方の公式って??
こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。
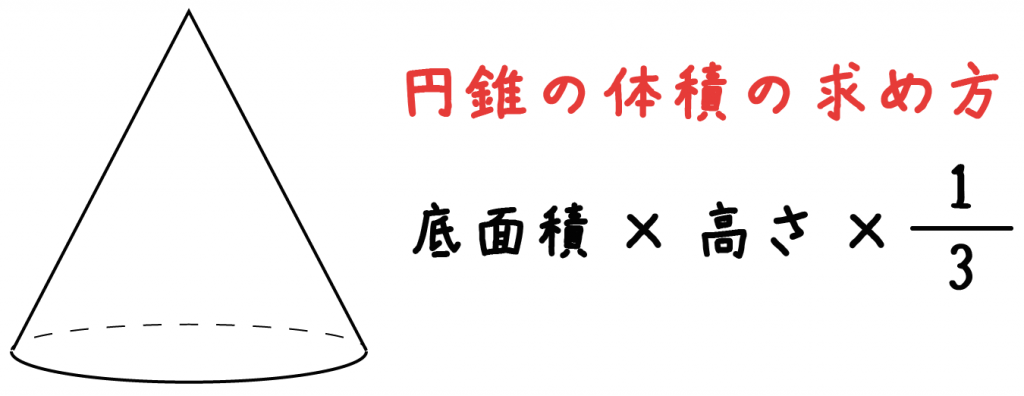
円錐の体積の求め方の公式は、
底面積×高さ×1/3
だったよね。
もう少し詳しくかいてあげると、
半径×半径×円周率×円錐の高さ×1/3
になるんだ。

これなら3秒で円錐の体積を計算できちゃいそうだね。
ただ、そのスピード感について来れないときもあるだろうから、今日は、円錐の体積の求め方をチョーゆっくり公式をつかってといてみるよ^^
「円錐の体積の求め方がどうしてもわからん!」
ってなったときに参考にしてみてね!
円錐の体積の求め方がわかる3つのステップ
円錐の体積の求め方はつぎの3ステップをで計算できちゃうよ^^
つぎの例題をときながらみていこう!
半径3cm、高さ10cmの円錐の体積を計算して^_^
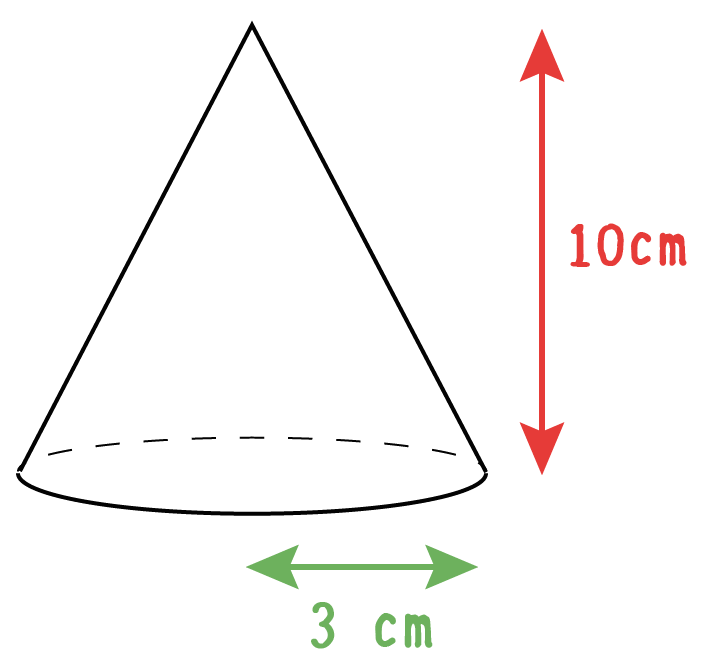
Step1. 円錐の「底面積」を計算するっ!
まずは円錐の底面積を計算してみよう。
円錐の底面は「円」になっているね。
ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。
円の面積の求め方は、
半径×半径×円周率
で求められるよね??
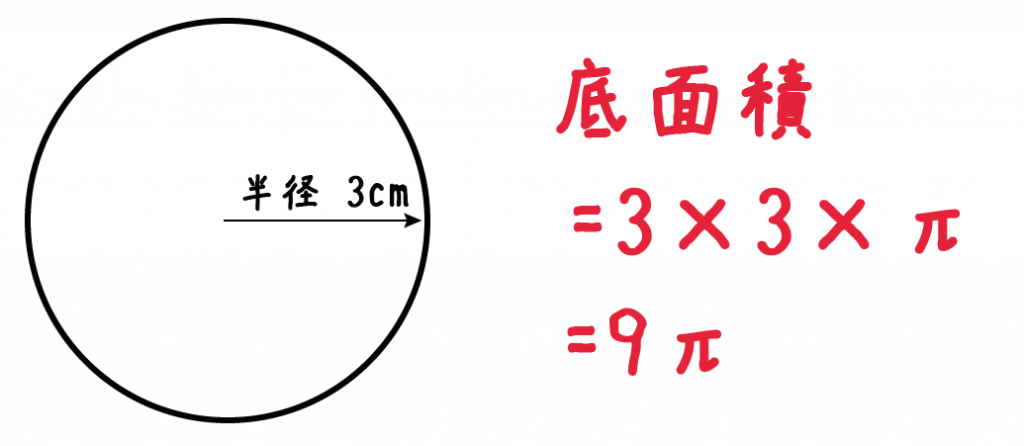
だから例題の円錐の底面積は、
3×3×π= 9π
となるんだ。
Step2. 円錐の底面積に「高さ」をかける!
つぎは「円錐の高さ」を底面積にかけてみよう。
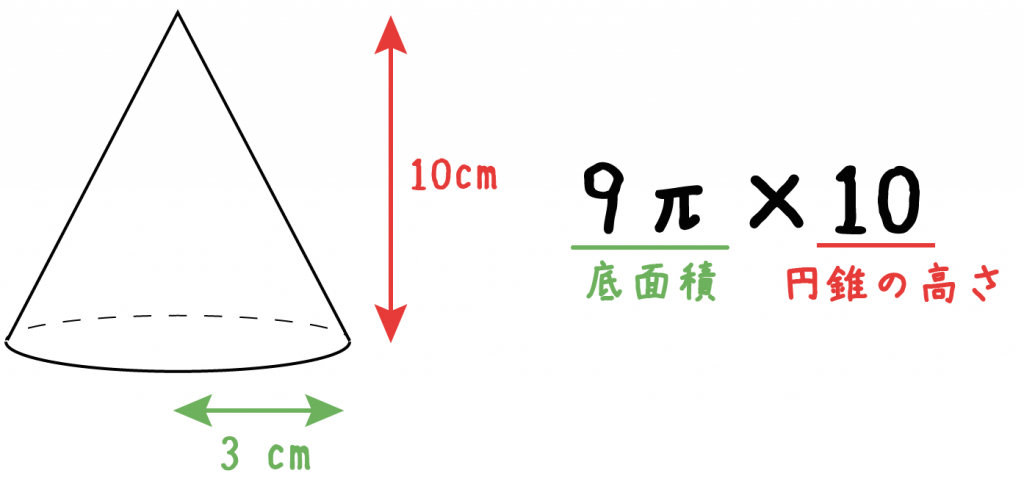
例題の円錐の高さは10cmなので、
9π×10= 90π
になるっ!
Step3. 「1/3」をかけるっ!!
いよいよ最後のステップ。
Step2で求めた「底面積×高さ」の値に「1/3」をかけてみよう。
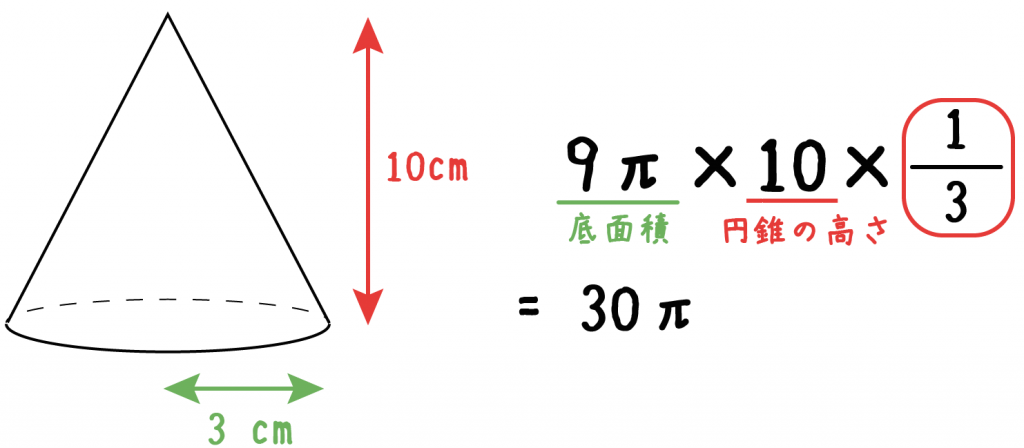
例題でいうと、「底面積×高さ」は「90π」だったから、
最終的な円錐の体積は、
90π×1/3=30π
になる!
おめでとう。これで円錐の体積を計算できるようになったね^^
なぜ「1/3」をかけるのか??
えっ。なんで「1/3」をかける必要があるのだって?!?
その理由は高校数学で勉強する「積分」を使えば説明できるんだけど、完全に中学数学の範囲をこえているんだ。
とりあえず、中学数学では、
錐体(先がとんがってるやつ)の体積を求めるときは「1/3」をかける
ということを覚えておこう。
だから、三角錐の体積を求めるときも「1/3」をかけるんだ^^
まとめ:円錐の体積の求め方の公式はシンプル
円錐の体積の求め方はどうだったかな??
底面積×高さ×1/3
という公式は意外とシンプルだったよね笑
最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。
分数がややこしかったら、「÷3」をするって覚えてもいいね。
この公式をつかってじゃんじゃん円錐の体積を計算していこう!
円錐の体積の求め方をマスターしたら、次は「円錐の表面積の求め方」を勉強してみよう。
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。






















1分の3をかけるときに約分して答えを出すんですか?
頭悪くてほんとにすみませんw
そのほかはとても分かりやすかったです!
>1分の3をかけるときに約分して答えを出すんですか?
そうだね!約分してるよ。
わかりづらかったら、「÷3」って覚えてもいいね
三角錐の求め方を教えて下さい!
三角錐の体積の求め方を読んでみて
円錐形に内接する球の半径の出し方
>円錐形に内接する球の半径の出し方
円錐を真っ二つにスパッと切った断面図をかいてみよう
円錐の投影図の問題で、
立面図→底辺8cm、面積36cm²
この時の円錐の体積を求めなさい、という問題がどうしても解けません。
教えて頂けないでしょうか
>円錐の投影図の問題で、
立面図→底辺8cm、面積36cm²
この時の円錐の体積を求めなさい
底辺と面積の情報から、立面図の三角形の高さを計算してみよう。
この高さは円錐の高さでもあるからね。
あとは円錐の体積の求め方で計算しよう
わかりやすかったです!
ありがとう!!
説明がとてもうまいですし、コメントへの回答も的確だと思いました。
ありがとう!!励みになるぜ!
円錐の展開図があって、側面となる扇型の母線が10cmで、底面の円の半径が6cmの場合の体積ってどうやって求めればいいですか?(この展開図を組み立てたときにできる円錐の体積)
倍を求める時、a.bは使いますか?
ありがとうございます!よく分かりました!特に尖ってるやつに1分の3かけるというとこです!
>円錐の展開図があって、側面となる扇型の母線が10cmで、底面の円の半径が6cmの場合の体積ってどうやって求めればいいですか?(この展開図を組み立てたときにできる円錐の体積)
三平方の定理を使って高さを求める問題だね。
三角錐の高さの求め方を読んでみて
三角形ACOがあってACを軸として回転させた体積を求める問題でその図形が円錐の底面積同士をくっつけた形なのですがどういう方程式を使えば答えが出せますか?
>三角形ACOがあってACを軸として回転させた体積を求める問題でその図形が円錐の底面積同士をくっつけた形なのですがどういう方程式を使えば答えが出せますか?
2つの円錐に分けて体積を計算するといいよ。
2つのコーンに分ける感じ
質問ではないですけれど、すごくわかりやすかったですありがとうございます。
これからも応援しています
ありがとう!!励みになるぜ!
これって中1でも円錐が出た時使っても可ですか?
>これって中1でも円錐が出た時使っても可ですか?
もちろん!
見た時はなるほどと理解できるのですが、
しばらくすると忘れてしまいます(>_<)
どうしたらいいですか?(>人<;)
>見た時はなるほどと理解できるのですが、
しばらくすると忘れてしまいます(>_<) どうしたらいいですか?(>人<;) 公式の類は日常生活に全く関係ないことだから普通に覚えようとすると忘れちゃう。 だから、最初は公式を見ながらでもいいから問題をたくさん解いてみよう。それで体に公式をしみこませよう
ありがとうございました=^_^=
とても参考になりました。❣
色々とKenさんの解説、見させていただいています!!!
体積って、計算ミス多いです。
どうすればいいですか?教えてください。
>体積って、計算ミス多いです。
どうすればいいですか?教えてください。
体積で忘れがちなのが錐の尖ってる立体の計算で最後に3分の1をかけ忘れることだよね。
とがってたら要注意だ
いつもわかりやすい説明ありがとうございます
とてもわかりやすくて、勉強がはかどりました!ありがとうございます!!!
円錐の求め方をどうしても忘れてしまうので助かりました!(σ*´∀`)
ありがとうございました
役に立ってよかった!!
yはxに比例し、x=12のときy=-9である。x=-16のときのyの値を求めなさいの問題がわかりません。答えを教えてください
yをxで割って比例定数を求めてみよう。
y=axのaだね。
で、そいつがわかったらy=axの式にx=-16を代入してyを求めてみよう
どうしても原価の問題が理解できないです
円錐の求め方がわかりやすかったです。初めて見たけどね(^ – ^)これからもよろしく((^_^)
商売の基本は
品物を原価で仕入れて、そいつに利益を乗っけて定価で売り抜けて儲けるってこった
なにこれ……めちゃくちゃわかりやすいんだが。
こんな馬鹿な私でも分かりましたありがとうございます(´TωT`)
ありがとう!
ありがとう!!
質問じゃないんですが、この記事、僕の苦手な数学の分野を簡単にかかれていてめちゃくちゃ分かりやすいです!助かってますm(__)m
めちゃくちゃ分かりやすかったです!!!!! (質問じゃないですが...)
これからも応援してます!!!
説明だけじゃなく、図もあるので助かりました!本当にありがとうございます!これからも頑張って下さい!!
参考になりました。kenさんありがとうございます。
すごく参考になりました!
頑張って宿題解いてきます,,,(/・ω・)/