二次関数・三角形・等積変形のトリプルアタック?
二次関数の問題では、なぜか三角形が絡んでくるけど、中でも厄介なのが、
「等積変形」を使った問題だ。
例えばこんなやつ↓
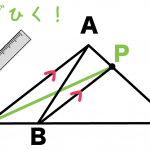
右下の図で、点A、Bは関数 y=ax² と直線 l のグラフの交点で、点Aの座標は(-2, 5)、Bのx座標は1である。y = ax² の x > 0 に点Pを、△POB=△AOBとなるようにとる。点Pの座標を求めて。

等積変形とは、
底辺が同じ2つの三角形の頂点が同じ平行線上にあると面積が等しくなる
ってやつだったね。
等積変形を忘れてたら復習してみてね。
この手の問題は5ステップで解けるよ。
Step1. 見通しをつける
最初に「大まかな流れ」を見通しておこう。
問題文では、
△POB=△AOBとなるようなPを求めなさい
といっているね。
ここで、等積変形の登場だ。
「OBに平行な直線」で、かつ、「Aを通る直線」を引いてみる。
その直線がy = ax² と交わるもう1つのAではない点が「P」になるね。

なぜなら、△POBと△AOBは辺OBを共有していて、かつ、高さが等しくなるからだ。
△POBと△AOBの底辺・高さが等しくなるから面積も等しくなるはず。

この「P」を求めればゲームクリアってわけ。
Step2. Bの座標を求める
まずはBの座標を求めよう。
B は y = ax² を通っていて、かつ、x座標が1。
ってことで、y = ax² にBのx座標「1」を代入すると
y = ax²
= a
が出てくるはず。
つまり、このaがBのy座標になるから、Bの座標は、
(1, a)
になるな!

Step3. OBの式を求める
ここでOBの式を求めよう。

OBの式を求める狙いは、
OBの傾きをゲットすること。
APとOBは平行だから傾きが同じになるはずだからさ。
ってことで、OBの傾きはAPの式を知るための手がかりなんだ。
何もビビることはなく、OBの式を求めるのはすこぶる簡単。
原点を通っている直線だから、OBは比例の関数だね。
で、比例ということは、その傾きに当たる「比例定数」は、
(yの増加量)÷(xの増加量)
で求められる。
Bの座標は(1, a)だから、原点からのxの増加量は「1」、yの増加量は「a」。
よって、OBの傾きは、
(yの増加量)÷(xの増加量)
= a ÷ 1
= a
つまり、傾きは「a」だから
y = ax
がOBの式になるはず。

Step4. APの傾きを求める
次はAPの傾きを求めるよ。
APはOBと平行な直線だから、傾きが等しい。
つまり、APとOBの傾きは両方「a」だ。

APの傾きもOBの傾きの「a」になるから、APの式の切片をbとすれば
y = ax + b
になるね。

Step5. APの式をaで表す
APの傾きはわかったから、あとはこいつに、
Aの座標(-2, 5)
を代入して切片bを求めてみよう。すると、
y = ax + b
5 = a × (-2) + b
b = 2a + 5
になる。
つまり、APの式は、
y = ax + 2a + 5
になる。

Step6. AP と y = ax² の交点を求める
次は y = ax² とAPの交点を求めよう。

求めるためには、
- y = ax²
- y = ax + 2a + 5
という連立方程式を作って解けばいいね。
すると、
ax² = ax + 2a + 5
になる。
Step7. aの値を求める
さて、ここがこの問題の一番のミソだ。
二次関数 y = ax² とAPは
- A
- P
の2点で交わっているね?

最初から「Aの座標」は(-2, 5)ってわかっていた。
これはなにを意味するのかというと、
- y = ax²
- y = ax + 2a + 5
を連立させてできた
ax² = ax + 2a + 5
の答えの1つはAのx座標の「x = -2」になるはず。
ってことで、すでにわかっているxの解「x = -2」を代入してaを求めよう。

ax² = a分の1 x + 2a + 5
a ・(-2)² = a分の1 × (-2) + 2a + 5
a = 4分の5
になるね。
いやあ、やっとaの正体がわかったぜ。
Step8. Pの座標を求める
二次関数 y = ax² とAPの交点を求める式の
ax² = a分の1 x + 2a + 5
に戻ってみよう。
こいつにaを代入すると、
4分の5x² = 4分の5 x + 2 × 4分の5 + 5
5x² – 5x – 30 = 0
x² – x – 6 = 0
(x-3) (x+2) = 0
x = 3, -2
になる。
x=-2はAのx座標だから、もう1つの「x=3」が「Pのx座標」のはず。

あとはPのy座標を求めればいいから、y = 4分の5x² に x = 3を代入して、
y = 4分の5x²
= 4分の5× 3²
= 4分の45
になる。
したがって、Pの座標は
(3, 4分の45)
だ!!
やった!やっと終わった!
まじなげえな!
もう解きたくねえな!
二次関数の等積変形を使った問題むずすぎ
こんな感じで、二次関数の等積変形を使った問題はちょっと難しい。
正直、息切れは避けられない。
この問題で大事なのは、
解き始める前に等積変形をどのように使うのか?
という見通しを立てることだ。
そして、そのシナリオに合うようにいろいろ条件を整えていけばいいんだ。
難易度が高い問題だけど挑戦してみてね。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






質問する