速さ・時間・道のり(距離)っていったい何なのだろう??
こんにちはー!さしみこんにゃくが好きなKenだよー 今日も一緒に中学数学の勉強をしていこう!!
方程式の文章題で「速さ」のやつを苦手って子が多いよね??
たしかに時速とか分速とか速さとかよくわからないし、図を描いても解けそうな気がまったくしてこない。これは弱ったね^^

あまり知られてないけれど、
速さの文章題をすばやく解くには、
速さ・時間・道のり(距離)
という3つを理解していることが必須になってくるんだ。だから、今日はこの「速さ」・「時間」・「道のり(距離)」を順番にゆっくりと説明していくね。
これらの3つを踏まえて「速さの公式」もおぼえてみよう。
記事を読み終わる頃にはきっと、文章題の速さ問題が得意になっているはずだよ!!
~もくじ~
- 道のり(距離)って何??
- 時間って何??
- 速さって何??
- 速さの公式って?
速さ・みちのり・時間の前に知っておきたいこと
「道のり」とか「速さ」とか「時間」はどんなときに必要なんだろう?? ふだん見かけないからちょっと気になるよね??
じつは、
「人やもの」が「地点A」から「地点Bまで」移動したときに必要なんだ。

たとえば、小学1年生の太郎くんが「自宅」から「図書館」へ自転車で移動した、
みたいにね。
この「移動のイベント」が発生したとき、「道のり(距離)」や「速さ」が必要になってくるんだ。
道のり(距離)ってなに??
最初に理解したいのは「道のり」の意味だね。
ずばり、
道のりとは、
ある人や物が移動した距離
のことなんだ。たとえば、さっきの例で、太郎くんが家から図書館まで移動したよね?? このときの「道のり」は「家から図書館までの距離」ってことなんだ。
調べてみると、家から図書館までの距離はちょうど2kmだっとしよう。

このとき、太郎君が移動した「道のり」は、
2km
ってことになるんだ。道のりも意外とカンタンでしょ??
時間ってなに??
次に「時間」ってなにかってことを見ていこう。
時間とはずばり、
ある人やものが移動した時間
のことだよ。たとえば、太郎君が2kmさきの図書館まで10分かかって自転車で移動したとしよう。

このとき、時間は「10分」ってことになる。だって、太郎くんの移動に10分かかってるからね。
これで時間と道のりはオッケーだね!!^^
速さってなに??
最後に「速さ」ってなにかってことを見ていこう。速さとは、
一定時間あたり進む距離
のことなんだ。ちょっとよくわからないね?? さっきの太郎君の例をみてみよう。
太郎くんは、
2kmを10分かけて移動した
よね??

これは間違いない。じゃあ、太郎くんは1分間あたりに何km進んだことになるかな??
そう、0.2kmだ。

2kmを10で割ると出てくる答えだね。なぜ10で割るのかっていうと、1分間あたりに進む距離を出したいからだ。
0.2kmを10倍すれば2kmになるよね?? つまり一分間に0.2kmすすむことができる速さで10分移動したってことを意味するんだ。
この場合は、一定時間を「1分間」としているね。このときの速さのことを「分速」っていうんだ。ぼんやりと覚えておこう!
速さの公式だって!??
これらを踏まえた上で「速さの公式」ってものが誕生する。
それは次の3つだ。
- (道のり)= (速さ)×(時間)
- (速さ)= (道のり)÷(時間)
- (時間)= (道のり)÷(速さ)

ちょっと公式が3つもあったら覚えにくいよね?? そんなときに使いたいのが次のアイテムだ。
名付けて、
速さ公式はやみ図
だ。

ちょっとドラゴンボールみたいに見えるけど、実際はもっとすごいものかもしれない笑
使い方はいたってカンタン。
求めたいものを指で隠すだけ。
たとえば、「道のり」を求める公式を知りたいときは、こうやって親指をつかって道のりの欄を隠してあげるんだ。

すると、「速さ×時間」っていう公式がでてくるでしょ?? これで「道のり」が求められるわけだ。
「速さ」も「時間」も同じように求めることができる。
「速さ」を求めたければ、「速さ」を指で隠したら「道のり÷時間」っていう公式が出現するし、

「時間」を隠せば、「道のり÷速さ」の公式がゲットできるんだ。

ね?? 便利でしょ! 速さの公式を忘れそうな時はつかってみてね^_^
次回は速さの単位について説明していくねー!!
それじゃねー!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。














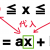












ある山の登山口から山頂までの山道を毎分60mの速さで登ると、毎分90mの速さでおりるのとでは、かかる時間が30分違うという。この山道の道のりを求めよ
>ある山の登山口から山頂までの山道を毎分60mの速さで登ると、毎分90mの速さでおりるのとでは、かかる時間が30分違うという。
この山道の道のりを求めよ
山道の道のりをxmとしてみよう。
あとは、行きと帰りでかかる時間の等式を作ればいいね
いつも参考にしてます!
ゎたしは、「サッカー部員にみかんを配るとき,1人に 12個ずつ配ると 19 個余り,1人に 14 個ずつ配ると 7 個足りない.このとき,サッカー部員の人数とみかんの個数を求めなさい」
この問題で
50(24-x)=2010-x
と式をたてました。でも、答えは間違っていました。なぜですか?ken様!
Aのプリンターは3分に18枚、Bのプリンターは5分に25枚印刷できます。どちらのほうが速く印刷できるでしょう?と、言う問題を教えてください
>「サッカー部員にみかんを配るとき,1人に 12個ずつ配ると 19 個余り,1人に 14 個ずつ配ると 7 個足りない.このとき,サッカー部員の人数とみかんの個数を求めなさい」
50(24-x)=2010-x
何をxにしたのかな?!
サッカー部員数をx人として、みかんの数に関する等式を作ってあげると方程式ときやすいよ。
>Aのプリンターは3分に18枚、Bのプリンターは5分に25枚印刷できます。
どちらのほうが速く印刷できるでしょう?
1分あたりに印刷できる枚数を計算してみよう。
プリントできる枚数を、時間の分数で割ればいいね
-x^2+6x-8
を因数分解したいんですけど、どうやるんですか?
x^2-8x=48
このような場合は、いちいち代入しないといけないの?????
>-x^2+6x-8
x2乗の前にマイナスがついてる時は、式全体をマイナスでくくってやるといいよ。
-(x^2-6x+8)にしてから、()の中身のx^2-6x+8をいつも通り因数分解してみて
x^2+6x-8
でも、因数分解出来なくないですか?
6xと-8だったら(+)2と3も使えないし…。
>x^2-8x=48
48を左辺に移項して、因数分解の解き方で解いてみよう
>x^2+6x-8
こいつは因数分解できないね。
ただ、-x^2+6x-8をマイナスでくくってやると、
x^2ー6x+8になるんだ。
こいつは因数分解できるはずだ
わかりました!
(x-2)(x-4)ですね!
回答ありがとうございました!
コメント失礼致します。
-x^2+8x=0
これは、一々代入して計算しないといけないのでしょうか?
>-x^2+8x=0
まずは両辺にマイナス1をかけてx2乗の前のーを消し去ろう。
あとは、共通因数xでくくってxの値を計算しよう
わかりました!
ありがとうございました。-8ですね!
ちなみに、かなちゃんが出てくる方の作者とkenさんが書いてる方の作者は一緒なのですか?
よかった!
いや、かなちゃんはつゆりささんが書いてるよ!
こんばんは。中間テストの勉強中に分からないところがあったので、
コメントさせていただきました。
(1)家と公園を往復しました。行きは分速50mで歩き、
帰りは分速125mで走ったところ、かかった時間は、
行きより帰りの方が9分短かったようです。
行きにかかった時間と、片道の道のりを求めなさい。
こちらの問題の求め方 テストに出た時に覚えておくと良いものを
教えてください。速さの公式は、ばっちり覚えています。
>(1)家と公園を往復しました。行きは分速50mで歩き、
帰りは分速125mで走ったところ、かかった時間は、
行きより帰りの方が9分短かったようです。
行きにかかった時間と、片道の道のりを求めなさい。
覚えておくのは方程式の文章題の解き方かな。
求めたいものを文字でおこう
速さはなぜ距離あたりの時間ではなく時間あたりの距離なのですか?
今回の例の場合、10分で2キロ進んだのだから1キロあたり5分かかる速さ
でも良いではないか と納得できません。
>速さはなぜ距離あたりの時間ではなく時間あたりの距離なのですか?
今回の例の場合、10分で2キロ進んだのだから1キロあたり5分かかる速さ
でも良いではないか と納得できません。
いい質問!確かにその通り!
ただそれだと、距離の単位に依存する速さになっちゃうのが難点かな。
距離の単位では日本のようにメートル法を採用しているところもあれば、アメリカのようにポンド法(マイル、ヤードなど)を採用しているところもあるし。
その点、時間あたりの速さなら万国共通ではある。
家から公園まで歩けば10分自転車では6分かかる。初めは、自転車にのり途中から歩いた。歩いた時間は自転車に乗っていた時間より2分長かった。
家から公園まで自転車で行くとき、1分間に進む道のりは家から公園までの道のりの何分のいくつか?
時速180kmのヘリコプターが45km飛ぶには何分かかりますか。(時速を分速に直して計算しましょう)
・この時分速に直すにはどうしたらいいでしょうか?
>時速180kmのヘリコプターが45km飛ぶには何分かかりますか。
まずかかる時間を時間で計算した方が早そう。
道のり÷速さ
=45÷180
= 4分の1時間
になるね。この4分の1時間を分に直してみよう
A町からB町を経てC町まで毎時40kmの速さで行くと1時間30分かかる。また、AB間を毎時30Km、BC間を毎時60分の速さで行くと1時間10分かかる。B町からC町までの道のりはA町からB町までの道のりの何倍か?
求め方を教えていただきたいです、
>A町からB町を経てC町まで毎時40kmの速さで行くと1時間30分かかる。また、AB間を毎時30Km、BC間を毎時60分の速さで行くと1時間10分かかる。B町からC町までの道のりはA町からB町までの道のりの何倍か?
A~Bをxkm、B〜Cをykmとして、2つの場合のかかった時間に関する連立方程式を作ってみようぜ
とても分かり易かったです。
最初の挨拶の「○○だね。」と「そんじゃねー」が好きです!
ありがとう!最初の挨拶するようにしようかな笑
90kmの距離を1時間30分かけて移動したとき速さは何km/hという問題が分からないのですが教えていただけないでしょうか?
1時間30分を1.5時間として計算するとわかりやすいな!
Aさんは学校へ行くのに分速80mで歩くと40分で着きました。Aさんが家を出た15分後に弟が追いかけて、最初分速100mで歩き、途中から分速240mで走りました。弟はAさんと同じ時間に学校に着きました。
歩いた距離は何メートルになるんですか?
教えてください!
170km離れたA町とB町がある。松村さんは、時速50㎞の自動車でA町からB町へ向かって出発した。また、市川さんは、松村さんA町を出発してから15分後、時速40kmのバイクでB町からA町へ向かって出発した。2人が出会うのは松村さんがA町を出発してから何時間後か。 という問題はどう解けばよいですか?
最近、腕につけるタイプのデバイス(腕時計ではない)を使用しているのですが、機能の結果が相対的なので、そのデバイスの論理を自分なりに理解しようと思い、この公式がどういう公式なのか知りたくて、このサイトにたどり着きました。
この公式もどういう論理なのか気になるところです。
何故、この公式を小学校で習うんだろう??
忘れてもいい公式だからですかね??
大体、小学校で習ったことは忘れるものだと思っているのですが、最近、教育ってなんだろうなとも思ってます。
やや固定
÷ ÷
ベクトル × 相対的
しかも、これを算数で習う。
こういうことを考えなくてもいい忙しさが欲しいです。(子ども)質問らしい質問してなく、すみません。
麓から山頂まで分速40メートルで昇るのと同じ道は山頂からふもとまで分速60メートルで降るのとではかかる時間が30分違います麓から
山頂までの道のりは何メートルでしょうか
は、どうやってといたらいいですか?