比例・反比例の利用の文章題をすばやくときたい!
こんにちは、ホットミルクで目を覚ますKenだよ。
中1数学の「変化と対応」で最後に登場するのは、
比例・反比例の利用
というモンスターだね。ここでは、
比例や反比例を利用して日常生活の問題を解決していこう!!
っていう勉強をしていくんだ。いままでならってきた比例や反比例がちょっと身近に感じられるかもね。

でも、ちょっとむずかしくて苦戦することも多いから、
今日は、
比例・反比例の利用の文章問題をスマートにとく2つの方法
を紹介していくね。テスト前によかったら参考にしてみてね^^
比例・反比例の利用にみられる2つの問題の種類
比例の利用、反比例の利用ってむちゃくちゃ難しくみえるよね。
でもよーくみてみると、じつはたった2つしか問題の種類がないことがわかる。
それは、
- yとxの関係(比例か?反比例か?)が書かれた問題
- yとxの関係が書かれてない問題
の2つさ。

これだけじゃ、ちょっとわからないから例題をみながら確認していこう!
問題1. 「yとxの関係がかかれた問題」
この手の問題では、
yはxに比例する
だとか、
体重はモテる度合いに反比例する
だとか、
問題に登場する関数が比例するのか、反比例するのかあきらかにしているんだ。
たとえば、次のような問題があったとしよう。

風呂掃除をした時間をx分、もらえるお小遣いをy円とすると、yはxに比例する。このとき、80分働いたとき800円もらえたとすると、400分はたらくといくらお小遣いをゲットできるでしょうか。
この問題では「yはxに比例する」と問題の中でネタバレしてしまっているね。この手の問題はつぎの2つの手順でとくことができるんだ。
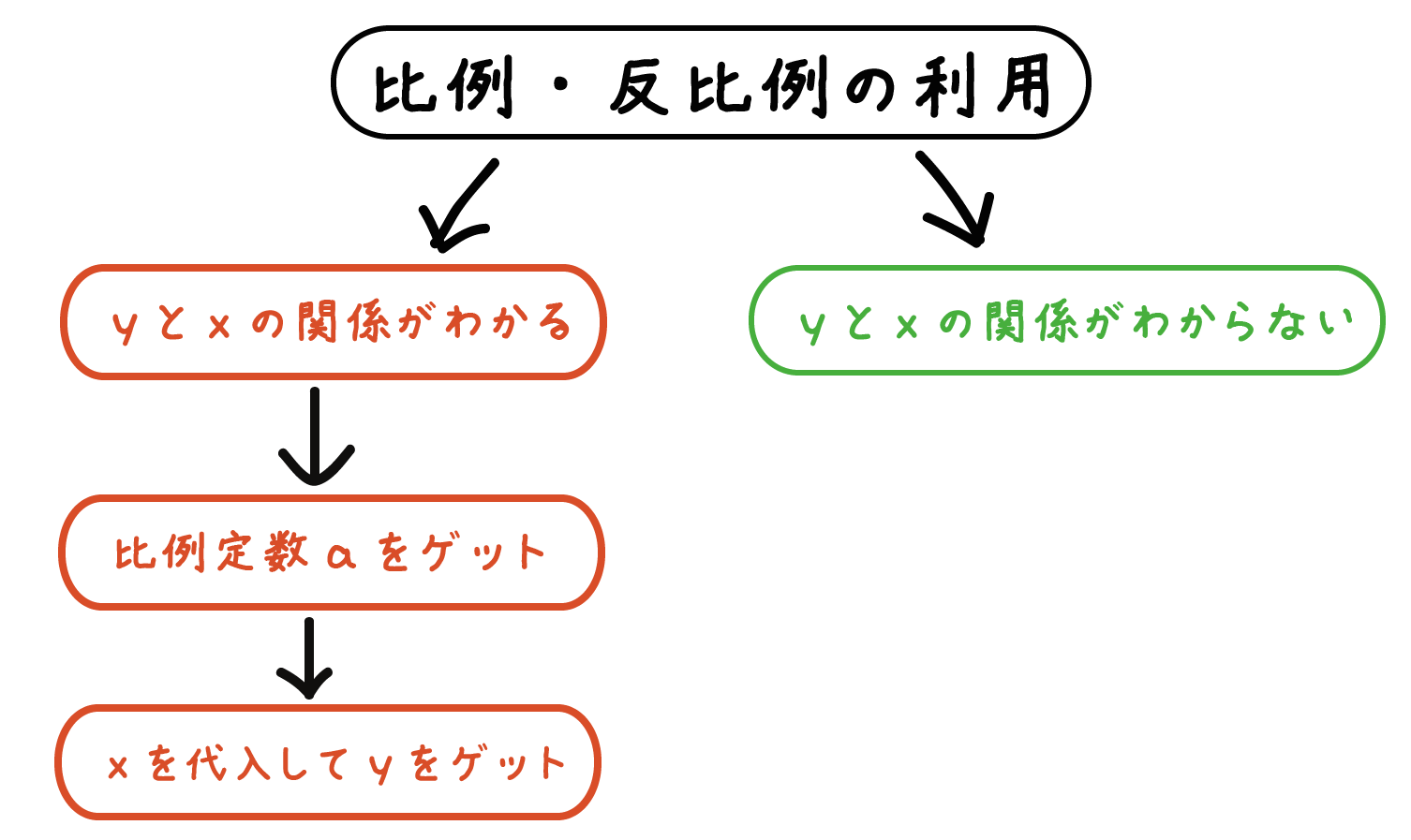
- 比例定数aを求める
- xに値を代入してyを求める
手順1. 比例定数aを求める
yとxの値がわかっているし、yとxの関係(比例か反比例か)もわかっている。
それじゃあ、比例定数aを求めてみよう!
さっきの例題だと、
- yはxに比例している
- x=80のとき、y=800
という情報がわかっているので、
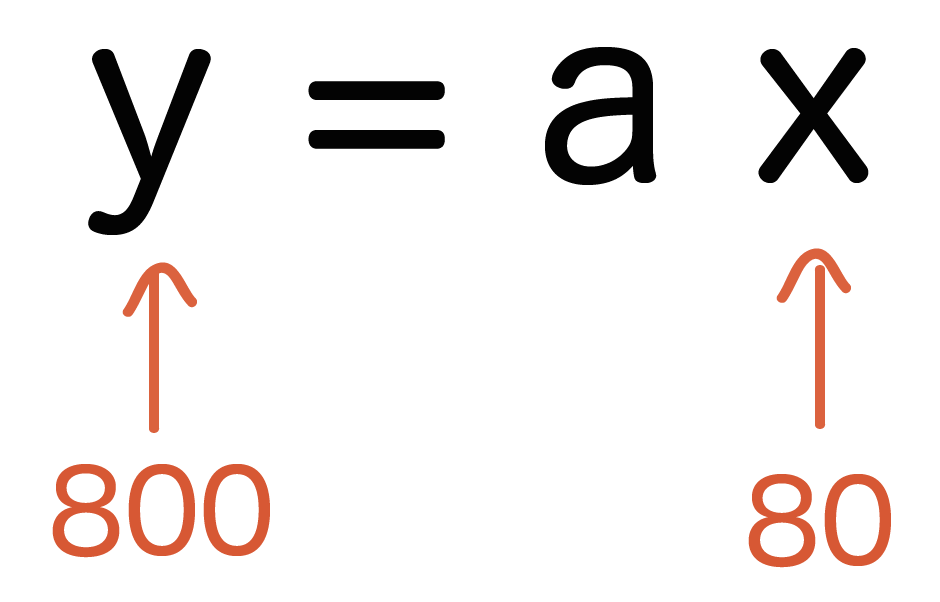
800 = 80a
という計算式がたてられるね。そんで、比例定数aを計算してやると、
a = 10
になる。
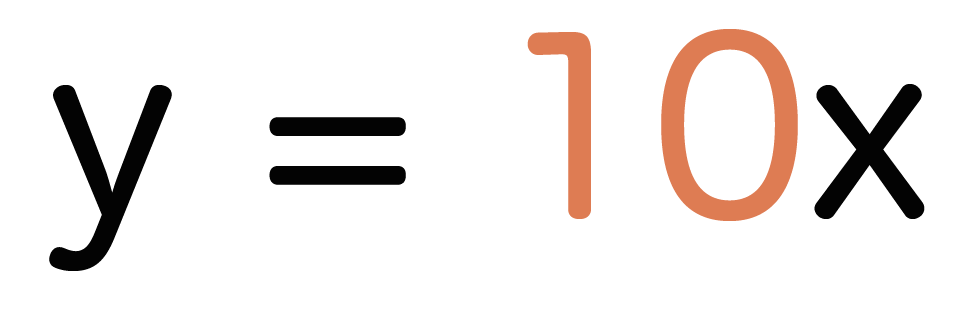
これで第一ステップが終了だ。
手順2. xを代入してyを求める
この手の問題の場合、
xがある値をとったときのyの値
をきいてくることが多い。
さっきの例題でいうと、
x = 400のときのyの値だね。
よって、さっきの比例関数 y =10x にx = 400を代入してやると、
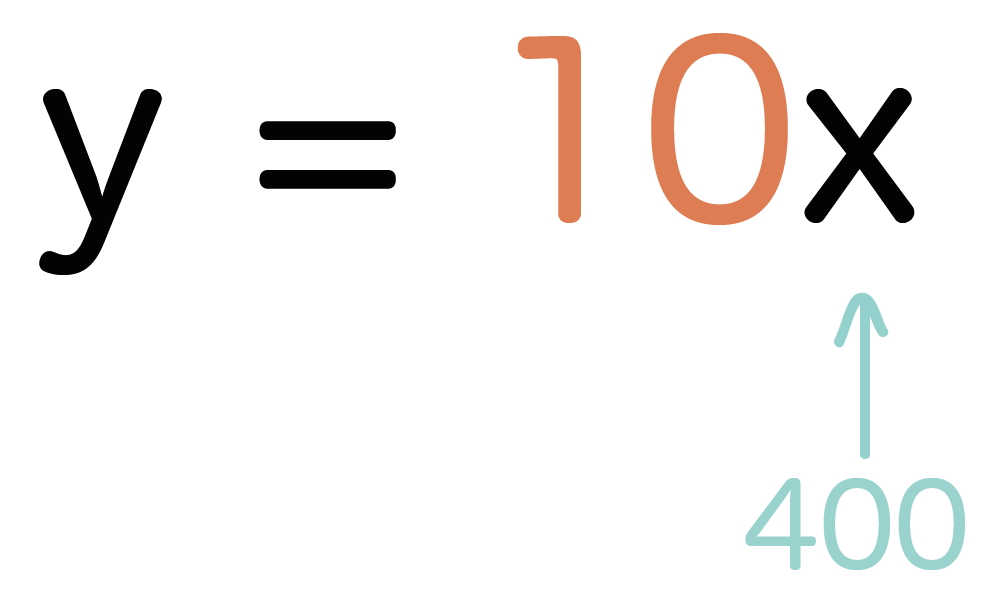
y = 4000
という値がゲットできるね。
つまり、この小僧は400分風呂そうじをして4000円稼ぐことができたってわけ。
以上が1つめの解き方だよ。どう??納得した??
問題2. 「yとxの関係が書かれていない問題」
2つ目の問題は「yとxの関係がかかれていない問題」だ。
つまり、yとxが比例するのか? 反比例するのか?? ということが文章問題の中でいっさい触れられていないということ。
この手の問題はつぎの2つの手順によってとけちゃうんだ。
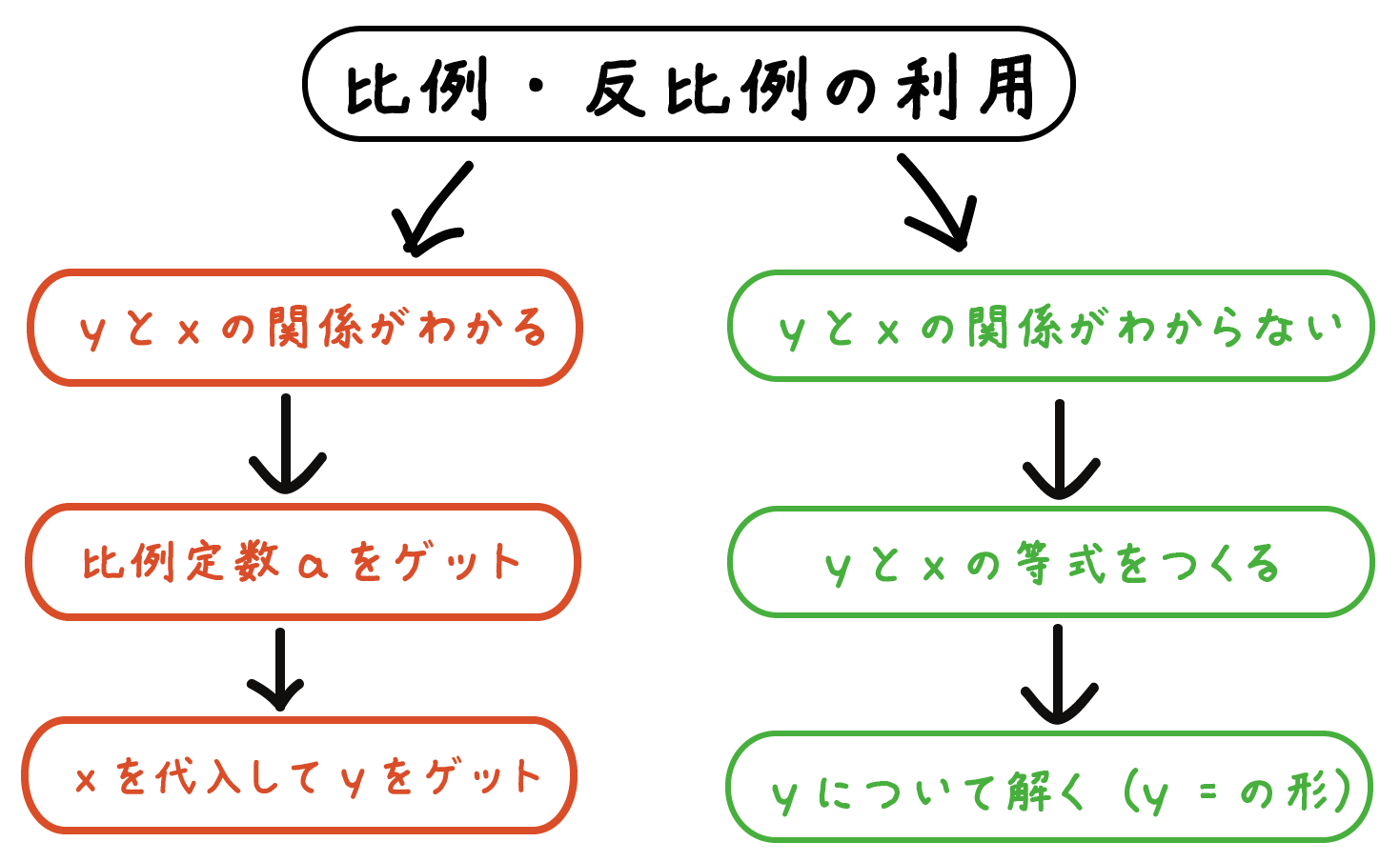
- yとxで等式をつくる
- yについて解く
さっきの問題よりむずかしくみえるけど、案外たいしたことないよ^^
つぎの例題をみながら解き方を確認していこう。

50Lの水がはいる金魚鉢に毎秒xLのペースで水を補給していくとy秒でいっぱいになって金魚が逃げてしまう。このとき、yとxの関係を式であらわしてくれ。
というもの。
このタイプの問題はつぎの2ステップで解くことができるんだ。
手順1. 「yとxで等式をつくってみる」
この手の問題では、
とりあえずyとxの関係を等式であらわしてみる!
というチャレンジ精神が大切だ。比例になるか、反比例になるかわからなくても前に進んでみよう。
さきの例題では、「毎秒x L でy秒水をいれると50Lの鉢がいっぱいになる」ので、
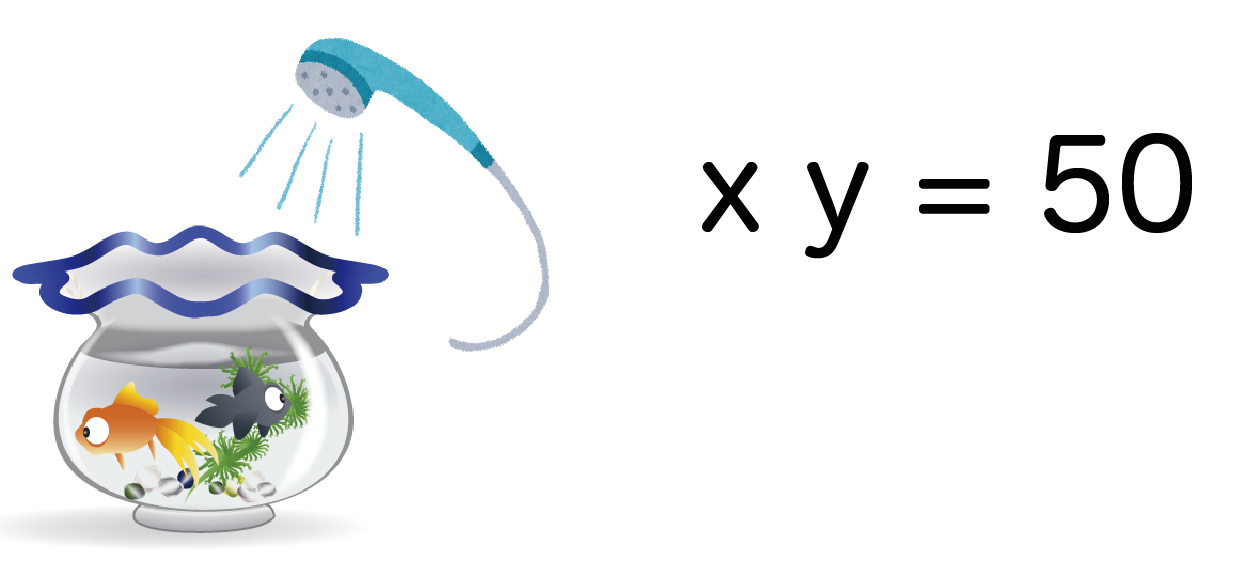
xy = 50
という等式がたてられるはずだ!
これが第一ステップだね^^
手順2. 「y = 」のカタチに変形する
つぎは、その等式を、
y = ○○○○
というカタチに変形してあげよう。等式の左辺に「y」という文字をもってくればいいだけさ。ね??カンタンそうでしょ。
さっきの例題の「xy = 50」でいえば、
両辺を文字「x」でわってみよう。すると、
y = 50/x
というカタチに変形できるはずだ。
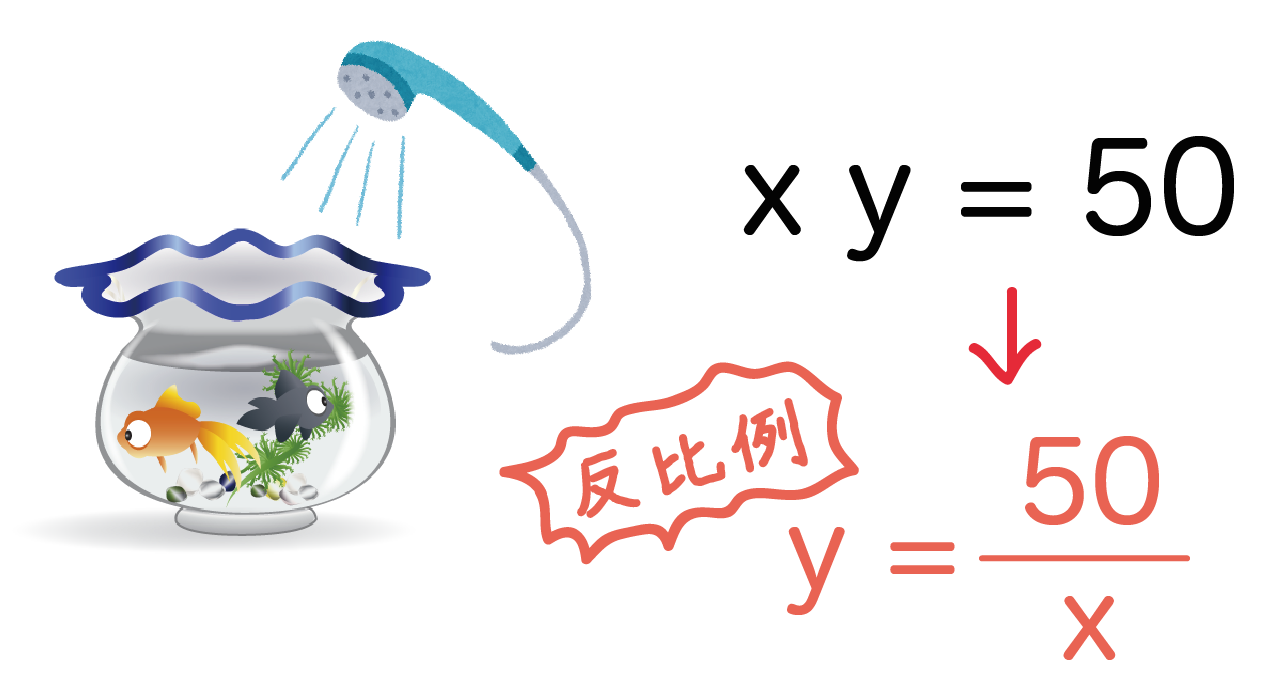
これはなんという偶然なことか、反比例の式のカタチ
y = a/x
にそっくりだね笑
ってことで、この問題では反比例の関数を利用していたことになるんだ。
まとめ:比例・反比例の利用の問題は2つに分類すればOK
比例・反比例の利用は上の2つの方法でとけば大丈夫。
中1数学の「変化と対応」ではちょっとむずかしいところだけれど、ゆっくりとけば答えがみつかるはず。
テストでも落ち着いていこう!
次回はいよいよ平面図形の勉強に入っていくね^^
そんじゃねー!!
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





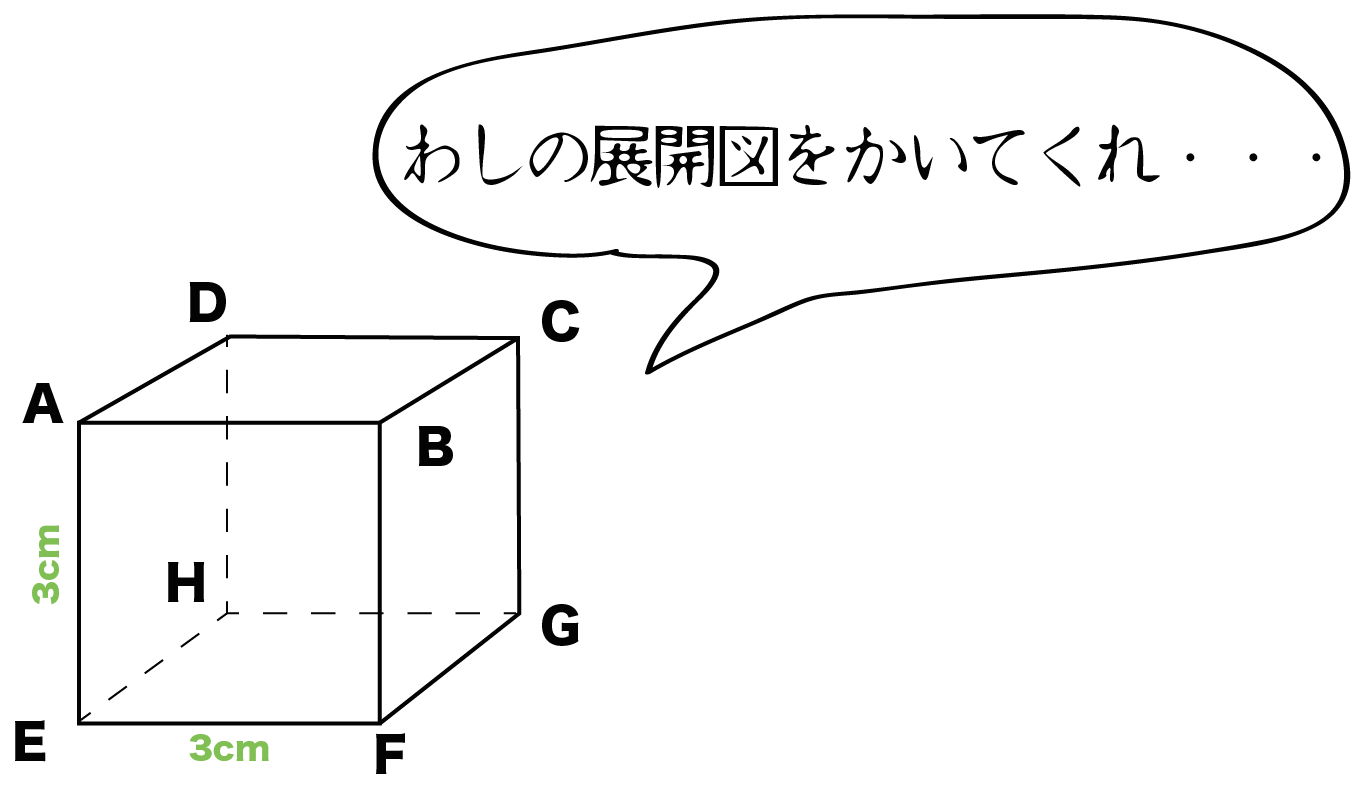

数学の中1の、1学期の問題教えてください
マイ病0.4リットルずつ水を入れると90秒出いっぱいになろ水槽があるこの水槽を24びょうでいっぱいにするには毎秒何リットルずつ水を入れれば良いですか
>マイ病0.4リットルずつ水を入れると90秒出いっぱいになろ水槽がある
この水槽を24びょうでいっぱいにするには毎秒何リットルずつ水を入れれば良いですか
まずは水槽の体積を「マイ病0.4リットルずつ水を入れると90秒出いっぱい」から計算。
あとは、その体積を時間で割ればいいね
座標が分かりません
次のとき、yを xの式で表しなさい。
・ x:5=y:10
・ x:(yー3)=3:1
・ x:( x + y)=5:8
…という問題があるのですが、解き方がわかりません。
教えてください。
>・ x:5=y:10
・ x:(yー3)=3:1
・ x:( x + y)=5:8
これは比例式の解き方と同じでいいよ。
内向の積 外向の積で計算して比の形を一旦無くしてやろう
比例の、y=3分の2Xがよくわからないのですが、どうすればいいでしょうか?
>比例の、y=3分の2Xがよくわからないのですが、どうすればいいでしょうか?
比例のグラフのかきかたかな?
原点と、x・y座標が整数になる点を結ぼう
ある薬品80mLの重さが100gであった。この薬品48mLの重さは何gか。
とういう問題がわかりません
教えてください
>ある薬品80mLの重さが100gであった。この薬品48mLの重さは何gか。
とういう問題がわかりません
1mLあたりの重さを計算して、それに48をかければオッケー
水槽に水を入れるとき同じホースを3本使うと満水になるまで20分かかる。ホースを1本だけにすると水槽が満水になるまで何分かかるか?の問題が分からない
>水槽に水を入れるとき同じホースを3本使うと満水になるまで20分かかる。ホースを1本だけにすると水槽が満水になるまで何分かかるか?の問題が分からない
ホース1本の場合に、満水になるまでの時間を計算しよう。
具体的に言うと、時間をホースの本数で割ればいい
比例式がつくれません。文章題のどこを見れば良いのでしょうか?
>比例式がつくれません。文章題のどこを見れば良いのでしょうか?
とにかく、yとxの関係を式に表せればオッケーかな。
比例なら自然とy=ax形になるはずだ
60L入る空の水槽に、毎秒6Lの割合で水を入れる。水をいれ始めてからx分後の水槽の水量をyLとしてyをXの式で表しなさい。
という問題があるのですがわかりません…教えて下さい。
>60L入る空の水槽に、毎秒6Lの割合で水を入れる。水をいれ始めてからx分後の水槽の水量をyLとしてyをXの式で表しなさい
1分間に6L入るから、x分後は何L入る?それがyだ!
あとは水槽は60Lしか入らないから変域にも注意してね
反比例のグラフを上手に書く方法が分からないので教えてください
>反比例のグラフを上手に書く方法が分からないので教えてください
反比例のグラフのかきかたを読んでみて!
反比例のグラフと関数グラフの違いが分かりません。
教えてください、、。
>反比例のグラフと関数グラフの違いが分かりません。
教えてください、、。
反比例は関数の一種。
反比例がチワワなら関数は犬だ。
厚さが一定のアルミ板から下の図の二つの形を切り取りました
(ア)
長方形 横15cm
縦10cm
(イ)
長野県
(ア)の板の重さが24グラムの時
(イ)の板の面積は、どうすれば求められるでしょうか
y=x分の8のグラフがあります。このグラフの点P
(x>0)からx軸、y軸に垂直な直線PQ、PRをひきます。このとき、長方形OPQRの面積はつねに一定になります。座標の1目もりを1㎝として、その面積を求めなさい。この問題の答えが8平方センチメートルになる理由がわかりません。教えて下さい。
>y=x分の8のグラフがあります。このグラフの点P
(x>0)からx軸、y軸に垂直な直線PQ、PRをひきます。このとき、長方形OPQRの面積はつねに一定になります。座標の1目もりを1㎝として、その面積を求めなさい。この問題の答えが8平方センチメートルになる理由がわかりません。教えて下さい。
Pのx座標をaと置いて、Pのy座標をaで表してみよう。
Pのx座標は長方形の横の長さ、y座標は縦の長さになってるはずだ。
あとは長方形の面積の求め方で計算してみよう
2点(9、d)、(3、d+4)は、同じ反比例のグラフ上にある。dの値を求めなさい
>2点(9、d)、(3、d+4)は、同じ反比例のグラフ上にある。dの値を求めなさい
反比例の式のy=a/xに2点の座標を入れて、aとdについて連立方程式を作ってみよう
どうしよう。
比例、反比例の式が分かりません…
比例、反比例のグラフの書き方も分かりません…
YはXに比例し、Xの値が三増加するとき、Yの値は4減少します。このときYをXの式で表しなさい。
という問題がわかりません!!
比例の文章題と反比例の文章題の見分け方が分かりません。
教えてください。
>比例、反比例の式が分かりません…
比例、反比例のグラフの書き方も分かりません…
まずは比例定数の求め方をマスターしよう!
式がわかればグラフの書き方は簡単!
>YはXに比例し、Xの値が三増加するとき、Yの値は4減少します。このときYをXの式で表しなさい。
比例定数は、
(yの増加した数)÷(xの増加した数)
で計算できるよ。
ポイントは減少した時は負の数が増加したと考えることかな
>比例の文章題と反比例の文章題の見分け方が分かりません。
教えてください。
この手の問題は一旦、yとxの関係を等式に表せばいいよ。
あとはxとyの位置関係で比例か反比例なのかを判断していこう
比例・反比例の良さって何ですか?
>比例・反比例の良さって何ですか?
問題の解きやすさが良いとすると、項がxとyの2つしかなくて計算しやすいね。
一次関数とかになると、切片っていう奴が絡んでくるからちょっと厄介になる
比例の表の書き方が全くわかりません教えて頂けませんか?まだ小6で習っていないんです。
関数などはよく分かりました!ありがとうございます
>比例の表の書き方が全くわかりません教えて頂けませんか?
比例のグラフは直線になるよ。
直線ってことは、2つの点を結べばかけるね。
まず1つは原点(0,0)、もう一個はどこでもよくて、xとyの両方が整数になる点かな。この2点を直線で結べばかけるはず!
比例の式と反比例の式はどうやればいいですか?
yはxに反比例し、x=5のときy=4
という問題がわかりません!教えてください!
>yはxに反比例し、x=5のときy=4
という問題がわかりません!教えてください!
反比例の比例定数の求め方をマスターしよう。
簡単にいうと、xとyをかけると比例定数が出る
yはxー2に比例し、x=3のときx=4であった。
x=5の時のyの値を求めなさい
これわかります?
>yはxー2に比例し、x=3のときx=4であった。
x=5の時のyの値を求めなさい
まずは比例定数を求めてみよう。
y=a(x-2)の比例の式にxとyの値を代入してaを求める。
aが求まったらx=5を代入してその時のyをゲットしよう
比例と反比例の利用問題がわかりません。
助けて下さい。
生徒10人で体育館にイスを並べることにしたが、10人だと1人あたりが並べるイスの数が多いので、1人あたりが並べるイスの数を、10人のときの3分の1になるようにしたい。何人の生徒で並べればよいですか?
解き方がわかりません(๑• – •`๑)
>比例と反比例の利用問題がわかりません。
助けて下さい。
xとyで等式を作ってみて、あとはそこから比例なのか反比例なのかを判断すればいいよ。
あとは問題をたくさんといて出題パターンになれることかな
>生徒10人で体育館にイスを並べることにしたが、10人だと1人あたりが並べるイスの数が多いので、1人あたりが並べるイスの数を、10人のときの3分の1になるようにしたい。何人の生徒で並べればよいですか?
一人当たりが並べられる椅子の数をx、y人の生徒で並べるとしてみよう
3mの重さが240gで、100gあたりの値段が150円の針金がある。
1200円でこの針金を何m買うことが出来るか。
わかりません!
教えてください
>3mの重さが240gで、100gあたりの値段が150円の針金がある。
1200円でこの針金を何m買うことが出来るか。
1mあたりの重さ、1円あたり買うことができる重さを計算してみよう。
あとはそいつらと1200円をかければいいはず
理解できません( i _ i )
分かりやすかったです!
yはxに比例しx=6のときy=−4という問題がわかりません。是非教えてください
>yはxに比例しx=6のときy=−4という問題がわかりません。是非教えてください
yをxで割って比例定数を求めてみよう!
接線とは何ですか?
接線とは、ある図形に一点で接している直線のことだよ
y=ax+5みたいな式は比例にならないのですか?
そいつは一次関数っていうくくりになる。なぜなら、原点(0,0)を通ってないから
「A,Bそれぞれの板の重さが7g、5gのとき、Aの板の面積を求めなさい」という文章題がわかりません。どうすればいいですか?
たぶんもうちょっとヒント必要やな
「文房具屋にノートを買いに行った。手持ちの金額で、安いノートは8冊買えて
40円余る。このノートより60円高いノートは5冊買えて10円余る。安いノート1冊の値段と
手持ちの金額を求めなさい」という問題がわかりません!教えてください。お願いします
一次方程式の問題かな?
記事で解説してみるぜ!
同じダンボール紙から図1の正方形(100cm2)は8グラム図2(猫の形)は36グラムだった。図2のダンボール紙の面積は何cm2か
という問題が分かりません!
1gあたりの面積を求めて、そいつを猫の重さにかけるといいな!
y=axのグラフ上に2点(6,-10),(b,15)があるとき,bの値を求めなさい。
の求め方が分かりません。教えて下さい。
自然数xの約数の個数をy 個とする時yはxの関数か
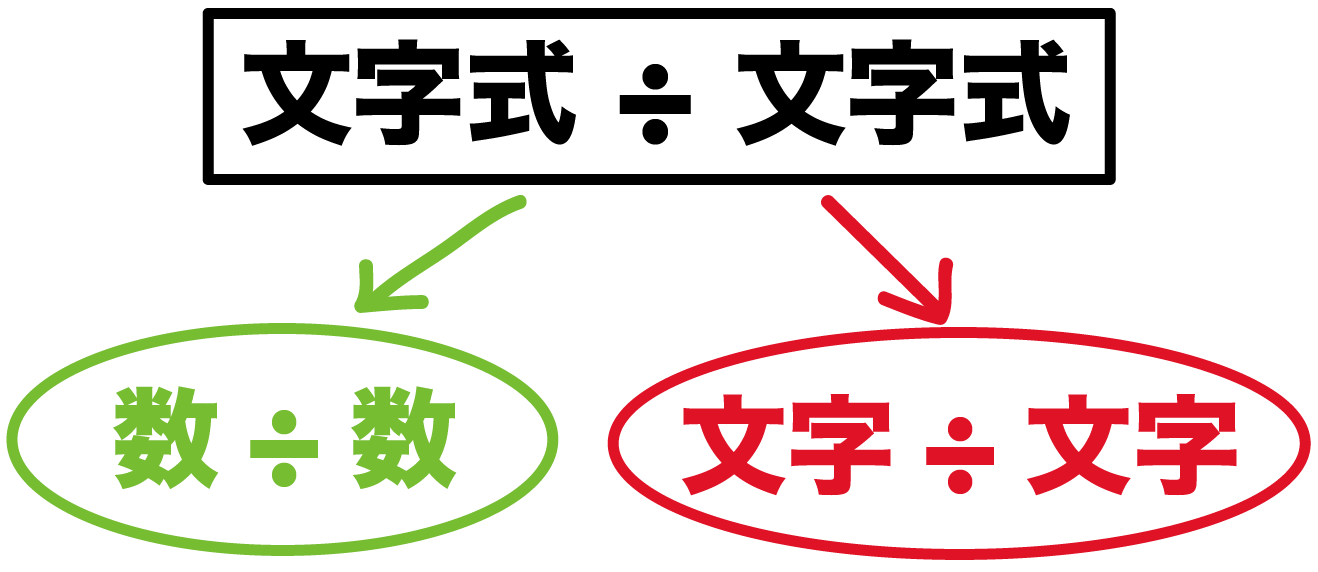
中学1年生では,文字式を文字式で割る(今回だと50=xyをy=50/xに変形すること)を学習しておりません。この場合,この方程式の解き方についてどのように指導したらよいでしょうか。
何歳ですか?