反比例の比例定数の求め方ってどうやんの??
こんにちは、カフェでコーヒーを頼まないKenだよ。
前回は「反比例とはなにか??」ということを勉強してきたね。反比例は比例とおなじように、関数の中の1種類だよ。
むずかしそうに聞こえるけど、基本をおさえればカンタンになってくるんだ。

今日は、反比例の問題でよくでてくる、
反比例の比例定数の求め方
をわかりやすく解説していくね。
コツさえつかんじゃえば、2秒ぐらいで比例定数を計算できるはずだ!!
2秒でできる!反比例の比例定数の求め方
反比例の比例定数の求め方はチョーシンプル。
比例定数の求め方とはずばり、
xとyをかけるだけ
だよ。

ね?? むちゃくちゃカンタンそうでしょ??
反比例の問題では「x」と「y」の値があたえられているから、その2つをかけあわせるだけでいいんだ。
反比例の比例定数を求める例題をみてみよう!!
実際の反比例問題で比例定数を求めてみよう!
つぎの問題があったとしよう。
yはxに反比例し、x=5のときy =6です。xとyの関係を式にあらわしなさい。
解き方:
問題の最初で「yはxに反比例する」っていってるね?? だからこのxとyについての関数の比例定数は、
比例定数 a = xy
で求めることができる。

そんで、
問題文をよーく目をこらしてみてみると、
x = 5, y = 6
ってことがわかるね。だから、反比例の関数の比例定数は、

xとyをかけあわせて、
30
になるね!
ね?? かけ算が得意だったら2秒で比例定数を求められたでしょ??笑
なんで反比例の比例定数がカンタンに求められるのか??
反比例の比例定数の求め方って、
a = xy
って超シンプルだったね。

じゃあ、なんでこんなカンタンなんだろう???
その答えは、
反比例の式をゆっくり変形すればわかるよ!

反比例の式である「y = a/x」の両辺にxをかけてみよう!!
すると、

分母の「x」があたらしくかけられた「x」と打ち消しあうっちゃうから、

この反比例の関数は、
a = xy
って変形できるね。

え?? あまりピンとこない??
そういうときは「等式の性質」をみなおしてみてくれ! 等式の基本さえわかっていれば大丈夫。読みながらもう一度変形にチャレンジしてみてね。
まとめ:反比例の比例定数はxとyをかけるだけでOK!!
ここまでみてきた反比例の比例定数の求め方はどうだった??
xとyの値をかけるだけだから、気合いをいれれば2秒ぐらいで求められるはず!!
つぎは、
反比例のグラフの書き方について勉強していくね^^
そんじゃねー!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。


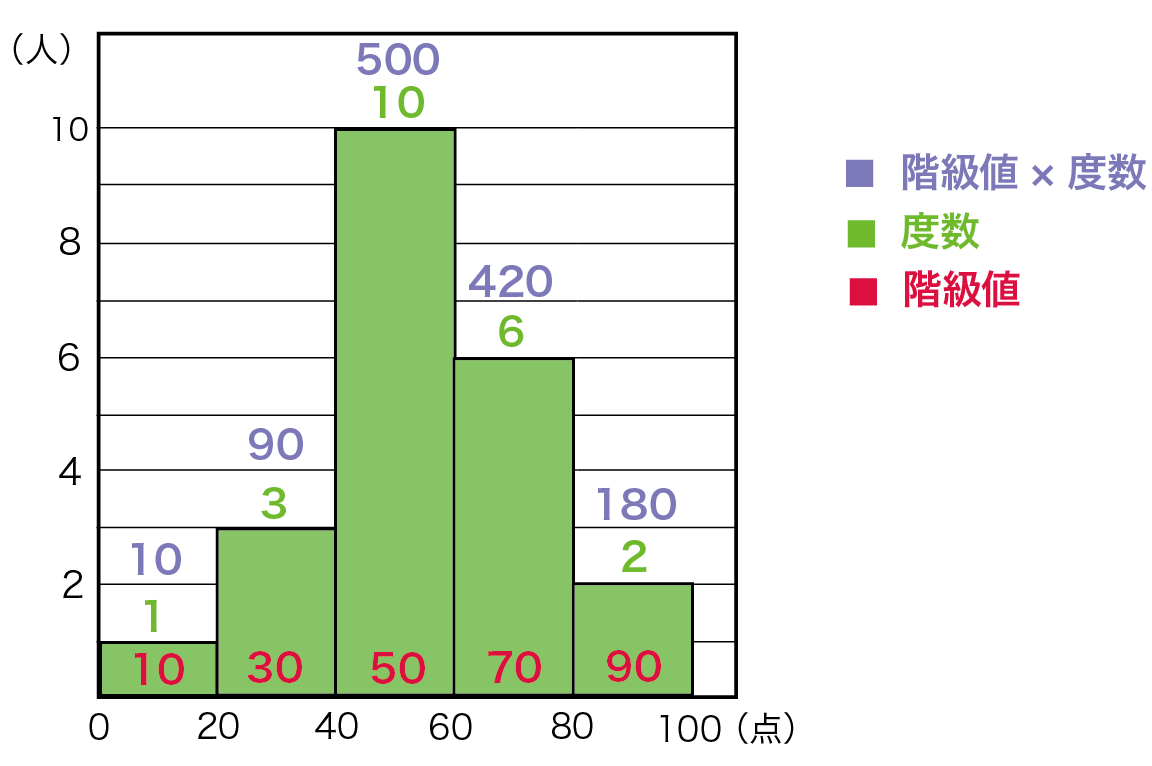

























一次関数の増加量について
y=-x/3
y=1/x
y=-2/x
の比例定数はなんですか?
y=-x/3は比例。
y = ax のaに当たるのはどれ?
y=1/x
y=-2/xは反比例。
y = a/xのaに当たるのはどれかな?
関数Y=a/xにおいて、xの値が-3から-2まで増加する時の変化の割合が-3/2の時、定数aの値を求めよ。
上記の問い、ご教授いただければ幸いです。
>関数Y=a/xにおいて、xの値が-3から-2まで増加する時の変化の割合が-3/2の時、定数aの値を求めよ。
ポイントはこの関数は反比例ってことだね。
xの座標が-3、-2のときのy座標をaで表してみよう!
そのy座標の差が-3/2になるっていう方程式作ればオッケー
反比例で変化の割合が xは 1以上3以下 yは-18以上-9以下のときって、
どう考えますか?
>反比例で変化の割合が xは 1以上3以下 yは-18以上-9以下のとき
変化の割合を求める問題かな?
変化の割合は、
yの増加量÷xの増加量
だから、まずはxとyの増加量を計算する必要があるね
Kenさん、この問題の解き方が分かりません、教えてください! 次のx、yの関係を式に表せ。また、yがxに反比例するものにはその比例定数を、反比例しないものには×を書け。
内のりが縦10cm横8cm深さ6cmの直方体の形をした容器に毎秒xcm3の割合で水を入れるとy秒間で満水になる。
>内のりが縦10cm横8cm深さ6cmの直方体の形をした容器に毎秒xcm3の割合で水を入れるとy秒間で満水になる。
まずは直方体の体積を計算してみよう。
毎秒xcm3で入れると、1秒でx、2秒で2x、・・・・ってことはy秒では体積はいくらになる?
こんにちは!コーヒーが大嫌いな雷の音デス!!
kenさんいつも、わかりやすくて、助かっています
突然ですが、我は計算問題は、バッチリなんですけど、文章問題が、まったくといっていいほど
とけません!だからいつも計算問題でなんとか80点代をキープしています。このままじゃ、いつか転落しそうで心配です。どうしたらいいでしょうか?
>突然ですが、我は計算問題は、バッチリなんですけど、文章問題が、まったくといっていいほど
とけません!だからいつも計算問題でなんとか80点代をキープしています。このままじゃ、いつか転落しそうで心配です。どうしたらいいでしょうか?
文章題は何回もといて慣れていくしかないね!
あとは状況がわからなかったら文章で言われていることを図で整理していくといいかも
yはxに反比例し、xの値が1から5まで増加するとき、yの増加量が−8である。この時の比例定数がわかりません。答えは10なんですが教えてください
>yはxに反比例し、xの値が1から5まで増加するとき、yの増加量が−8である。この時の比例定数がわかりません。答えは10なんですが教えてください
yがbから増加するとして、増加後のyの値をbを使って表してみよう。
あとはxの増加前の値とyの増加前の値を代入した時の比例定数、
xの増加後とyの増加後の値を代入した比例定数が等しいというbにかんする方程式を作ってみよう!
比例定数の求め方が問題集だとy=axなのですが‥‥なにかが違うのでしょうか?
>比例定数の求め方が問題集だとy=axなのですが‥‥なにかが違うのでしょうか?
比例と反比例では比例定数の求め方が異なるね!それは違うタイプの関数だから仕方がない!
比例の比例定数の求め方も読んでみて
比例定数(反比例)ってどう表すの?
y=x分のaのaが比例定数だよー
yはxに反比例し、x=6の時y=−2である。
x=−4の時yの値を求めよ。
っていう問題はどう解くんですか?
>yはxに反比例し、x=6の時y=−2である。
x=−4の時yの値を求めよ。
まずは「x=6の時y=−2」から反比例の式を求めてみよう。
あとはその式にx=-4を代入するだけ!
反比例の式で、比例定数が分数になることってあるんでしょうか?
>反比例の式で、比例定数が分数になることってあるんでしょうか?
あるんじゃないかなあー
(反比例)y=x分のaのaとそれの変化の割合は違うけど、
(比例)y=axのaとそれの変化の割合は等しい。
あってますか??
あってるよ!
こんにちは(^ ^)
今、 小6で中1の数学をやっているのですが、どうやったら
もっと数学への理解が深まると思いますか?
ただ問題が解けるだけじゃなくて
日常生活に結びつけてやると理解が深まるよ!
たとえば反比例だったら身近な反比例になっているものを見つけてみるとかね
反比例のグラフのかきかたが、いまいちピンとこないのですがどうすればいいのでしょうか?教えてください!お願いします!
xとyが両方整数の点を打ちまくって最後は雰囲気でむすべばOK
比例、反比例が利用されている身近なものって何かありますか?
比例定数意味わからん
コーヒーにはミルクと砂糖のヒプ民です!俺はケアレスミスをしやすいです…というか比例反比例の章が苦手です…この苦手をなくしたいのですがどうしたらいいですか?
問題をたくさん解いて慣れる!これが最短の攻略法!
いつもありがとうございます。これからも頑張ります!!!
いつもありがとうございます。
三平方の定理できる人が羨ましいです、、、
意味わからん、、、