円柱の体積の求め方の公式って!??
こんにちは、この記事をかいているKenだよ。アップルティーにはまってるね。
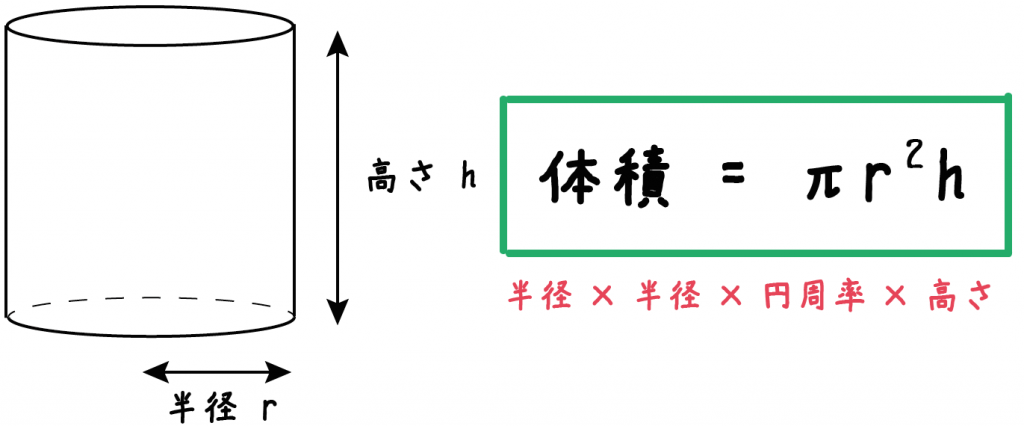
円柱の体積の求め方はむちゃくちゃ簡単。
底面積×高さ
っていう公式をつかえば、一発で体積を求めることができるんだ。
そんで、
底面積は、
半径×半径×円周率
だから、円周の体積はつぎの計算式で求められるよ。
半径×半径×円周率×高さ
円柱の体積の求め方がわかる2つのステップ
この公式をつかって円柱の体積を求めていこう!
次の2つのステップで「円柱の体積」を求めることができるんだ。
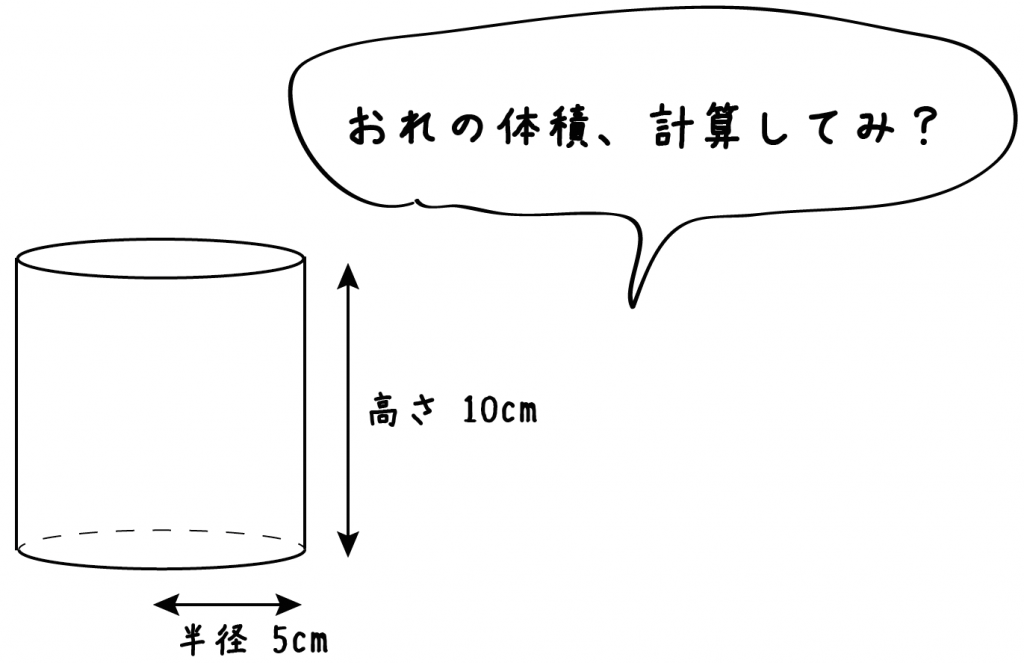
つぎの例題をみていこう。
底面の半径が5[cm]、高さが10[cm]の円柱の体積を3秒ぐらいでもとめてね!
Step1. 底面積を求める!
円柱の底面積を計算しちゃおう!
円柱の底面はもちろん「円」。
円の面積の求め方って「半径×半径×円周率」だったよね??
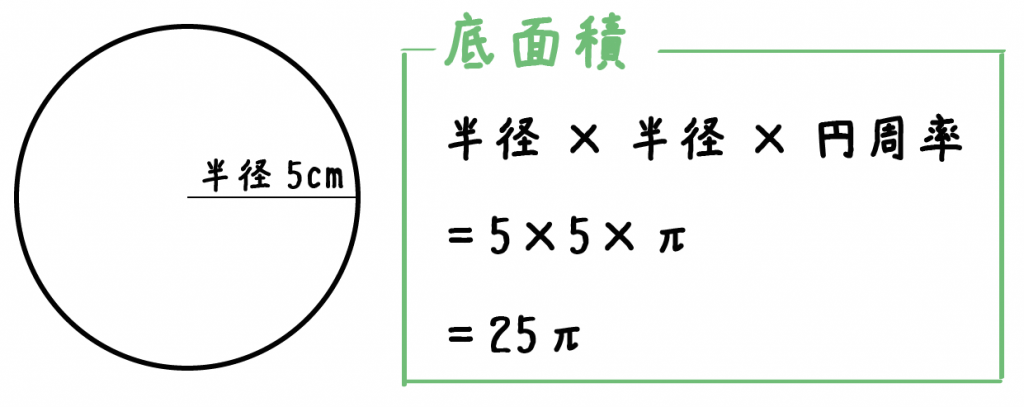
だから、例題の円柱の底面積は、
5×5×π = 25π [cm² ]
になる!!
Step2. 「底面積」と「高さ」をかける!
さっき計算した円柱の「底面積」と「高さ」をかけてみよう!
それが円柱の体積になるはずだ。
例題をみてみよう。
円柱の底面積は25π[cm² ]だったよね??
あとはコイツを「円柱の高さ」にかけてやればいいんだ。
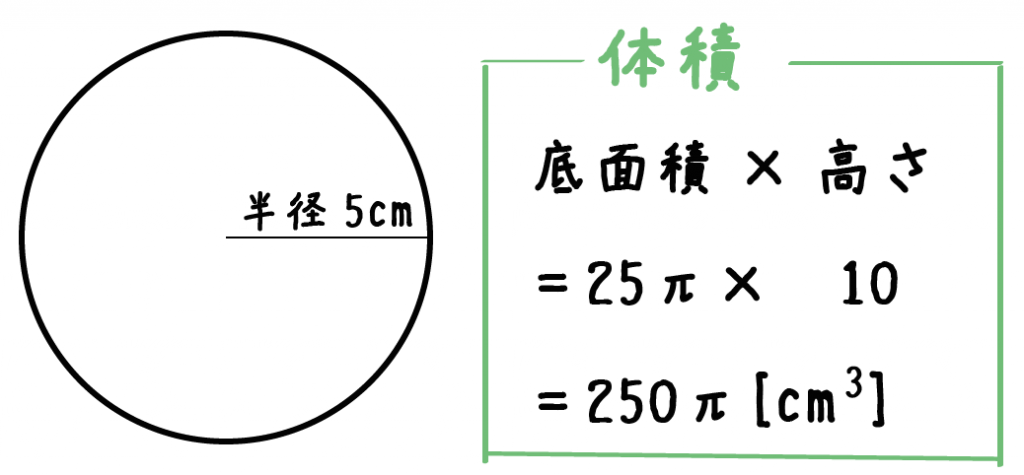
円柱の高さは10[cm]だから、
25π×10 = 250π [cm³]
になる!
これで円柱の体積の求め方はおわりだよー!!
まとめ:円柱の体積の求め方は楽勝すぎる!
円柱の体積の求め方はどうだったかな??
半径×半径×円周率×高さ

で円柱の体積は計算できたね。
円柱の体積を計算できるようになったらついでに円柱の表面積の求め方にもチャレンジしてみよう!
そんじゃねー!
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







円柱の表面積の求め方お願いします!!!!!!!!!!!!!!!!
円錐の表面積の求め方を読んでみて!
わかりやすかったです!!!!!
ありがとうございます
ありがとう!!!体積をガンガン計算していこう!
直径が1.2mで高さ30mの井戸に何立米はいりますか?
井戸は円柱ってことかな。
底面積を出して、それに高さをかけてみて
底面の半径がrcm、高さが4hcmの円柱Pと、円柱Pの底面の半径を3倍、高さを½倍にした円柱Qがある。
Pの体積はQの体積の何倍になりますか。
という問題がありまして…とても私の頭では求められそうにないので、恐縮なのですが、ヒントを頂けないでしょうか?
>底面の半径がrcm、高さが4hcmの円柱Pと、円柱Pの底面の半径を3倍、高さを½倍にした円柱Qがある。
Pの体積はQの体積の何倍になりますか。
円柱PとQの体積をrを使ってそれぞれ表してみよう。
ポイントは円柱Pの底面の半径をrでどう表すかかな。高さは円柱Pの高さを半分にしたやつだもんね
夏休みの宿題で「底面の半径がr㎝、高さがh㎝の円柱Aと、底面の半径が円柱Aの3倍で高さがAの三分の一の円柱Bがあります。円柱Bの体積は、円柱Aの体積の何倍ですか。」
という問題がでました。Bの体積の求め方を教えてください。
>底面の半径がr㎝、高さがh㎝の円柱Aと、底面の半径が円柱Aの3倍で高さがAの三分の一の円柱Bがあります。円柱Bの体積は、円柱Aの体積の何倍ですか
円柱Bの底面の半径と高さrとhで表してみよう!
あとは公式通りに計算するだけ
投影図が示されている問題です。
立面図とき四角形の縦と横の長さがどちらも
8㌢です。平面図円の半径の長さは書いてありません。
この時の体積は上にあるように半径が4㌢として
(π×4の2乗)×8=16π×8
=128π
の計算であってますか?
>投影図が示されている問題です。
立面図とき四角形の縦と横の長さがどちらも
8㌢です。平面図円の半径の長さは書いてありません。
この時の体積は上にあるように半径が4㌢として
(π×4の2乗)×8=16π×8
=128π
の計算であってますか?
あってるね!
4点a.b.c.dが同じ円周上にあるかどうか。
という問題の答えの解説で
2点d.cが直線a.bに対して同じ側にあり,
とあるのですが、同じ側にあるってどういう意味なんですか?
問題は「カゲロウデイズで中学数学が面白いほどわかる本>高校入試対策編<」のp.74の問2の(2)にあります。
円柱の高さの求め方を教えてください
わかりやすすぎー!
kenさんありがとうー
ありがとう!!
底面積はどう求めればよいのでしょうか?
円柱の求め方わかりやすかったです!
>底面積はどう求めればよいのでしょうか?
円柱の求め方わかりやすかったです!
円柱の底面は円だから、円の面積の求め方を使おう
半径6センチの球とその球がちょうど入る円柱、その円柱にちょうど入る円錐があります。このとき円柱、球、円錐の体積の比を求める。という問題で半径が6センチなのはわかるのですが、高さが何センチかの求め方がわかりません。答えには12センチと書いてありました。高さはどう求めるとよいのでしょうか?
>半径6センチの球とその球がちょうど入る円柱、その円柱にちょうど入る円錐があります。このとき円柱、球、円錐の体積の比を求める。という問題で半径が6センチなのはわかるのですが、高さが何センチかの求め方がわかりません。答えには12センチと書いてありました。高さはどう求めるとよいのでしょうか?
この様子を図に描いてみるといいよ。
球の直径が円柱の高さになってるはずだ
展開図が、一つの正三角形と、三つの二等辺三角形からなる立体があります。この立体の体積は何㎤ですか? (一辺は、6センチです。) という問題なのですが全く分からないので、教えて下さい。
>展開図が、一つの正三角形と、三つの二等辺三角形からなる立体があります。この立体の体積は何㎤ですか? (一辺は、6センチです。) という問題なのですが全く分からないので、教えて下さい。
どうやら三角錐になりそうだ。
三角錐の体積の求め方は(底面積)x(高さ) ÷3だから高さを求めればいい。
使うのは三平方の定理になりそう
円柱Pと円柱Qの体積の比を求めよ、という問題があるのですが答えやヒントなどがないので教えて下さい
円柱P:高さx cm、半径y cm
円柱Q:高さy cm、半径x cm
です。
>円柱Pと円柱Qの体積の比を求めよ、という問題があるのですが答えやヒントなどがないので教えて下さい
円柱P:高さx cm、半径y cm
円柱Q:高さy cm、半径x cm
です。
実際に体積をそれぞれ計算してみようぜ!
最後にそれを比にしてやればいい
円柱の容積の求め方?教えてください‼
直径10cmの円の面積の求め方、教えてください!
わかりやすい!
角錐の体積の求め方教えてください。
とてもわかりやすかったです! kenさんありがとうございました。
このサイトが一番わかりやすかったです。 ありがとうございました。これからも頑張ってください
このサイトが一番わかりやすかったです。 ありがとうございました。これからもこの公式を覚えてこれから出るテストなどに対策をしてせめて県立に行けるように努力をしたいです。
どうやって覚えら方法はありますか?