3分でわかる！相似比から体積の比・表面積比を求める公式

相似比から体積の比を求める公式ってあるの？？

こんにちは！ぺーたーだよ。

相似の単元の勉強はどうかな？？

相似の証明問題だったり、

相似比を求める問題が出たり

あれこれ大変だね。

今日はもう1つ新しい、

相似比をつかった体積の比の求め方

を解説するよ！

ついでに表面積の比の出し方も説明するから、

セットで覚えてあげよう。

相似比をつかって体積比を求める公式

相似比から体積比をだすときは、

つぎの公式をつかってみよう。

それは、

相似比の3乗が体積比になるよ

っていう公式だ。

くわしくいうと、

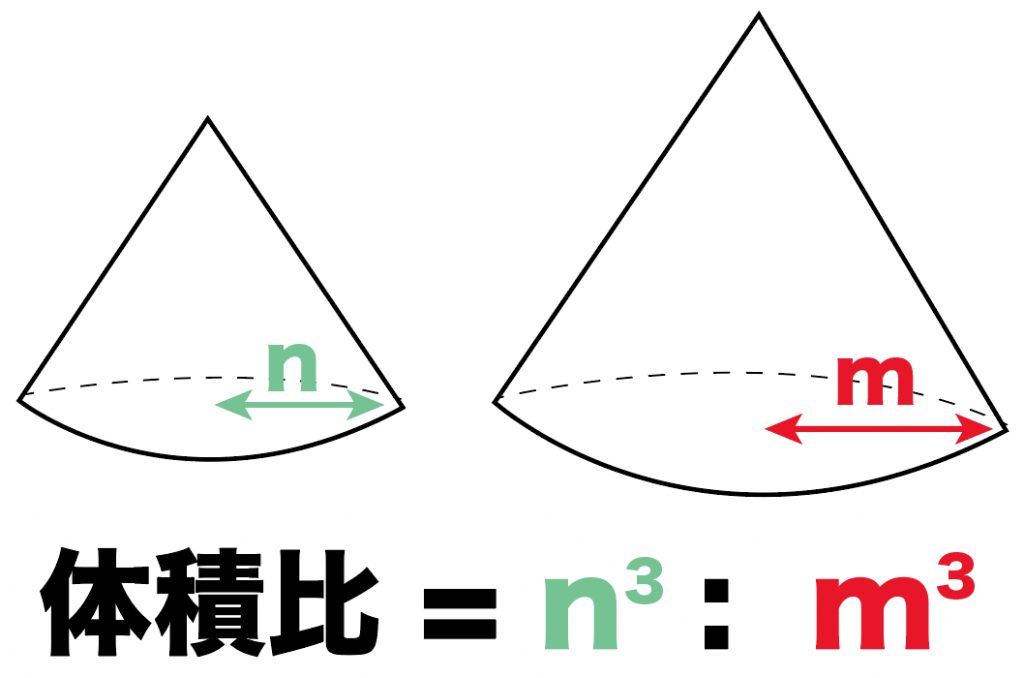
2つの相似な立体があって、相似比がn:mのとき、

2つの立体の体積比は、

n^3 : m^3

になるってこと。

この公式で練習問題をといてみよう。

練習問題

次の円錐は相似の関係です。

体積比と表面積の比を求めてください。

この体積比の問題は、2ステップでとけちゃうんだ。

Step1. 相似比を求めよう

立体の体積比を求めるには、

相似比

が必要なんだ。

練習問題をみてみると、

2つの円錐は相似である

ってかいてあるね。

わざわざ相似を証明する必要ないからうれしい！

さっそく相似比を求めてみよう。

対応する辺を「半径」として、相似比をもとめてみてね。

2つの円錐の底面の半径はそれぞれ、

• 2 cm
• 4 cm

だったよね？？

ってことは、こいつらの相似比は、

2: 4

= 1: 2

になるんだ。

Step2. 体積比を計算

相似比が出たら、

体積比はとっても簡単！

体積比の公式の、

相似比を3乗してやると体積の比になる

を使えばいいのさ。

練習問題でも体積比の公式をつかっていこう。

相似比は1：2っていうことがわかったね。

体積比はその相似比を3乗した、

1^3：2^3

= 1 : 8

になるね。

ってことで、

この2つの立体の体積比は「1 : 8」。

やったね！

体積比は何の役にたつの？？

えっ。

体積比は何の役にたつのかって？？

じつは、体積比がわかると、

「ある立体の体積」から「べつの立体の体積」が計算できちゃうんだ。

たとえば、さっきの練習問題で、

円錐Bの体積が80 [cm^3]だったとしよう。

この2つの立体の体積比は、

1: 8だったよね？？

ってことは、

「円錐Aの体積」は「円錐Bの体積」の8分の1。

ってことは、円錐Aの体積は、

（円錐Bの体積）×1/8

= 10 [ cm^3 ]

になるんだ。

ね？？

体積比をつかうと立体の体積がわかっちゃうんだ！

おまけ：相似比から表面積の比も求めてみよう！

相似比から体積比が求められたね！

おめでとう・・・・・・！！

っていうのはまだはやい。

じつは、練習問題の最後に、

表面積の比も求めなさい

ってかいてあるじゃん？

せっかくだから、表面積の比も相似比から計算してみよう。

ずばり、表面積の比の求め方は、

面積比の求め方といっしょ。

つまり、

相似比の2乗の比になってるのよ。

相似比が1:2の「円錐A・Bの表面積の比」は、

1^2 :  2^2

= 1 : 4

になるわけね。

もし、円錐Bの表面積が40 [cm^2]だったら、

円錐Aの表面積は10 [cm^2]

になるわけだね。

おめでとう！

相似比から表面積の比も求められたね！

まとめ：体積の比・表面積比の公式をしっかり覚えよう！

体積の比も、表面積の比も公式を覚えちゃえば楽勝。

しっかり公式を覚えてあげようね。

問題をときまくって段々なれていこう！

じゃあ、またね

ぺーたー

ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める