中央値(メジアン)の求め方がわからない??
こんにちは!この記事をかいているKenだよ。チャーハン炒めまくったね。
中学数学の資料の活用では、
中央値(メジアン)
を勉強するよね。
この単元はけっこうムズい。
メジアンとかモードとかわけのわからんカタカナでてくるし、
正直、わからんこと多いはずだ。
そこで今日は、苦手を克服してもらうために、
中央値(メジアン)の求め方がわかる3ステップ
を紹介するよ。
メジアンを出したいときに読んでみて^^
中央値(メジアン)の求め方・出し方がわかる3ステップ
さっそく中央値を求めていこう。
つぎの3ステップで計算できちゃうんだ。
- 大きい順にデータを並べる
- データ数が「偶数または奇数」か調べる
- 真ん中の値をみつける
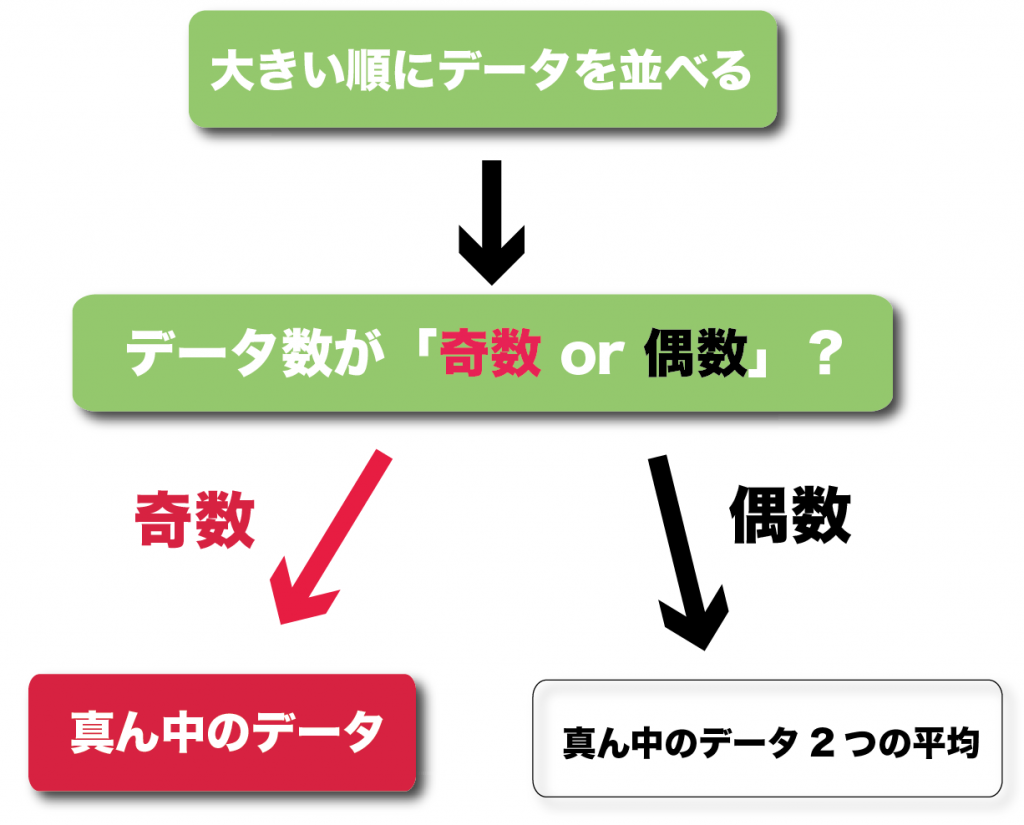
つぎの例題をといてみようね。
例題
下の表は、ある中学校の10人の生徒の砲丸投げの記録のデータです。10人の生徒の砲丸投げの中央値を求めなさい。
- Aさん: 7 m
- Bさん: 4 m
- Cさん: 5 m
- Dさん: 9 m
- Eさん: 11 m
- Fさん: 3 m
- Gさん: 4 m
- Hさん: 12 m
- Iさん: 6 m
- Jさん: 7m

Step1. 大きい順に並びかえる!
データを並びかえてみよう!
上から大きい順番にならびかえるんだ。
砲丸投げでスゴかったやつから順番にならびかえると、
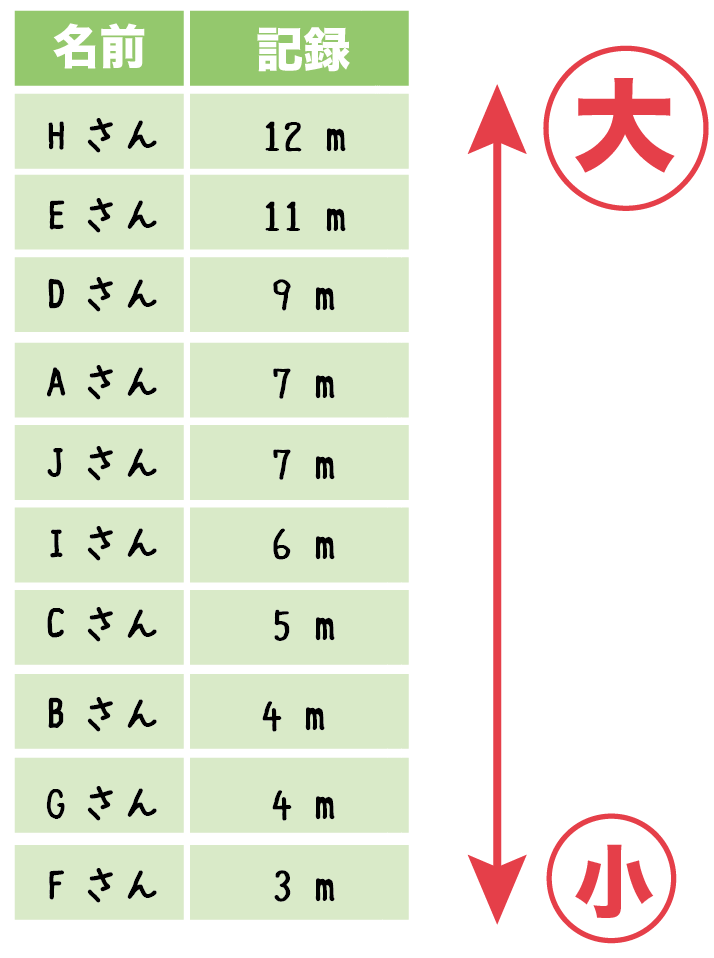
こんな感じになるね↓↓
- Hさん: 12 m
- Eさん: 11 m
- Dさん: 9 m
- Aさん: 7 m
- Jさん: 7 m
- Iさん: 6 m
- Cさん: 5 m
- Bさん: 4 m
- Gさん: 4 m
- Fさん: 3 m
Step2. データ数は「奇数or偶数」??
データの数をかぞえよう!
1、2、3、4・・・・
って感じでね!
ここでみてほしいのが、
データ数が「奇数」なのか「偶数」なのか???
ということだよ。
例題のデータは、10人の砲丸投げ記録だったね??
ってことは、
ぜんぶで10つのデータがあるわけだ。
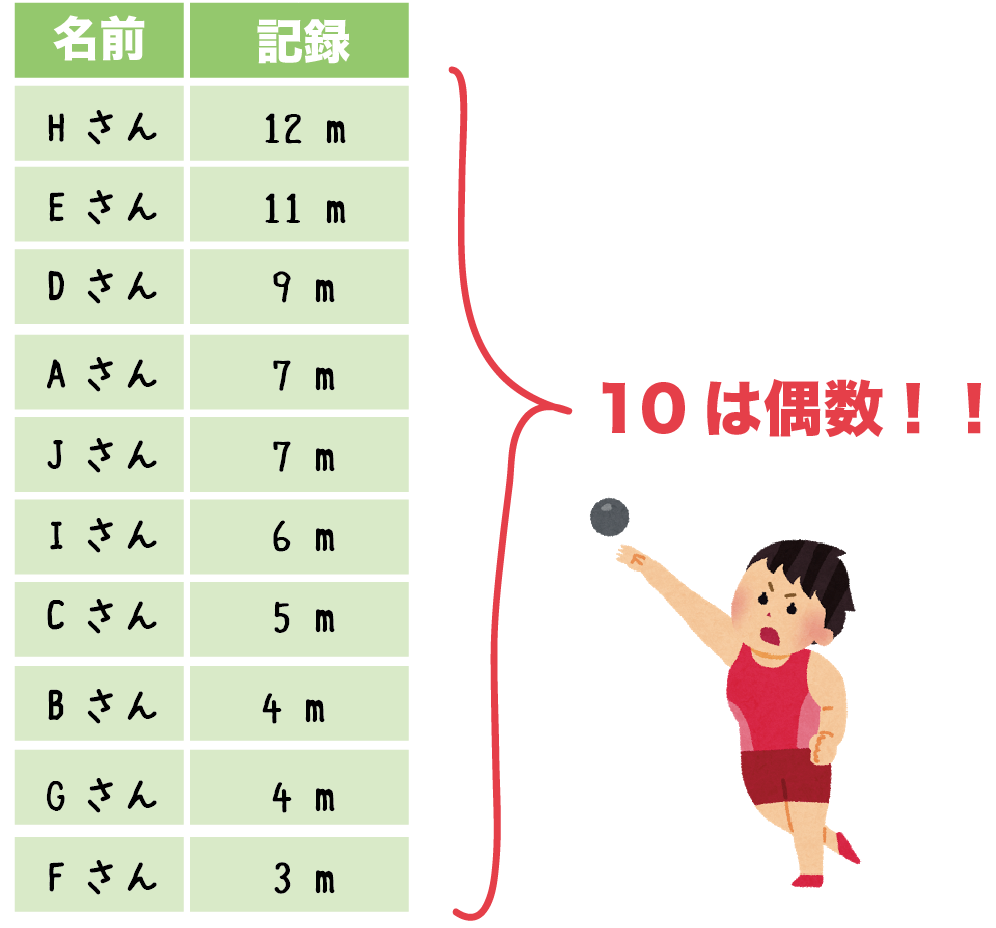
つまり、データ数は偶数だ!
Step3. 真ん中のデータをさがす
中央値は、
大きい順(or 小さい順)に並び替えたときの真ん中のデータ
のことだったね??
並び替えて真ん中のデータをえらべばいいわけさ。
ただ、注意してほしいのが、
データ数が「奇数」か「偶数」かによって真ん中の値の選び方がちがう
ってこと。
データ数が「偶数」のときは、
2つの真ん中の平均値をだすんだ。

真ん中の値は、
- Jさん: 7 m
- Iさん: 6 m
だね?
こいつらの平均をとってやると、
{(Jさんの記録) + (Iさんの記録)}÷2
= (7 + 6 ) ÷2
= 6.5
になる。
これが中央値だよ!

※データ数が「奇数」のときはどうする??
データ数が奇数のときはどうすんのって話だよね?
ちょっと気になる。。
さっきの例題で、Fさんが風邪で休んだとしよう。
すると、
砲丸投げをした生徒は9人になる。

つまり、データ数が奇数になるわけ。
奇数のときは偶数のときより簡単!
真ん中の数がそのまま「中央値(メディアン)」になるからね。
例題でいうと、
ちょうど真ん中の「7」がメジアンだ。
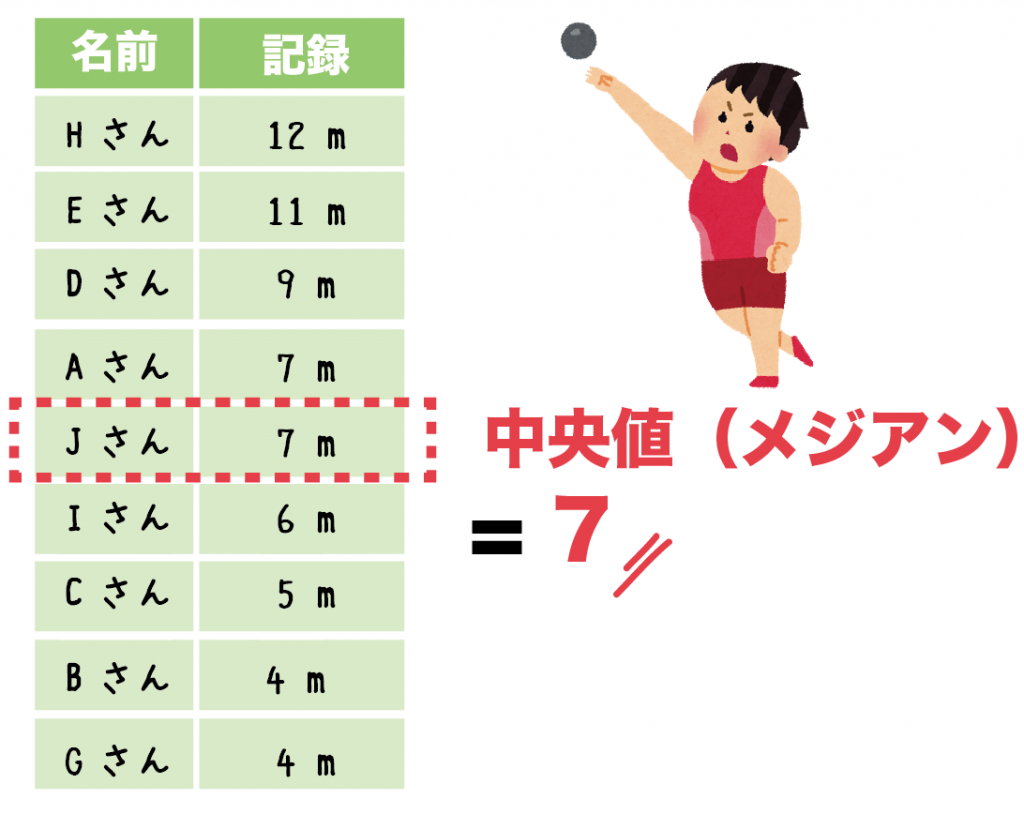
これで奇数のときも偶数のときも大丈夫だね!
まとめ:中央値の出し方は2通りある!
中央値の出し方には、
- データ数が「偶数」のとき
- データ数が「奇数」のとき
の2通りあるんだ。
- 大きい順にデータを並べる
- データ数が「偶数または奇数」か調べる
- 真ん中の値をみつける
という3ステップをおぼえちゃおう。
中央値なんてちょちょいのちょいさ!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。

























数学の問題です。
ある姉妹は2人合わせて2000円持っている。姉が妹に350円渡したところ、姉の持っている金額は妹が持っている金額の1.5倍になった。
この時、妹にお金を渡す前の姉の金額を求めなさい。
解説お願いします。
方程式の文章題だね。
問題で求めたいものを文字で置いてみよう。
この場合でいうと、「妹にお金を渡す前の姉の金額」だね。
あとは、「姉が妹に350円渡したところ、姉の持っている金額は妹が持っている金額の1.5倍になった」を等式にすればオッケー
10から20までの整数を10+11+…+20のように加える計算をしたところ、一か所だけプラスの記号を見落とし、4けたの数として計算して1848になった。見落としたプラスの記号はいくつといくつの間か。
一次方程式の問題で、答えは17と18です。解説を本当に詳しくお願いします。
>10から20までの整数を10+11+…+20のように加える計算をしたところ、一か所だけプラスの記号を見落とし、4けたの数として計算して1848になった。見落としたプラスの記号はいくつといくつの間か。
一次方程式の問題で、答えは17と18です。解説を本当に詳しくお願いします。
まずは10+11+…+20を計算するといくつになるか計算しよう。
そうすればどの数字を間違えたのかわかりやすくなるね
度数分布表での(偶数)中央値の求め方を教えてください。
度数が大きい順番に並び替えて、真ん中の2つの階級値の平均値をとってやればいいね
問題の説明すらできません。
x人いる…で、パッとなんばん目の人が中央値になるかわかる方法ありますか?
>x人いる…で、パッとなんばん目の人が中央値になるかわかる方法ありますか?
一瞬でわかる方法ないかも笑
度数が大きい順に並べてちょうど真ん中になってるやつが中央値だ
図1に示した立体A-BCDEは、AB=9cm、AD=7cm、BC=CD=DE=EB=4cm、∠ADC=∠ADE=∠CDE=90°の四角錐である。辺AB上にあり、頂点A、頂点Bのいずれにも一致しない点をPとする。点Pを通り辺BCに平行な線を引き、辺ACとの交点をQ、点Qを通り辺CDに平行な線を引き、辺ADとの交点をRとする。
次の問に答えよ
1.次の□の中の「お」、「か」に当てはまる数字をそれぞれ答えよ
図1において、AP=3cmのとき、線分QRの長さは「か」分の「お」cmである。
おねがいしますm(_ _)m
一次関数での質問です。
直線Y=3x-2に平行で、点(-2、4)を通る式。という問題の解き方がわからないです。
データの個数が偶数個で中央値が整数でない場合
そのデータの中央値の入る階級は小数点以下含む階級ということでいいのでしょうか。
例えば9人の記録の中央値だったら、(9+1)÷2=5で、大きい方から5人目だったり、奇数の時は、人数+1をして÷2をした数の人が中央値になる、であってますか?
>図1に示した立体A-BCDEは、AB=9cm、AD=7cm、BC=CD=DE=EB=4cm、∠ADC=∠ADE=∠CDE=90°の四角錐である。辺AB上にあり、頂点A、頂点Bのいずれにも一致しない点をPとする。点Pを通り辺BCに平行な線を引き、辺ACとの交点をQ、点Qを通り辺CDに平行な線を引き、辺ADとの交点をRとする。
次の問に答えよ
1.次の□の中の「お」、「か」に当てはまる数字をそれぞれ答えよ
図1において、AP=3cmのとき、線分QRの長さは「か」分の「お」cmである。
平行線に挟まれた線分の比を使っていくよ!
まずはAQ:ACを求めてみよう!それがわかれば、AQ:AC=QR:CDだから、QRの長さを計算できるね
>直線Y=3x-2に平行で、点(-2、4)を通る式
平行ということは傾きが等しいということ。
ってことで、y=3x+bになるはずで、この式に点(-2、4)のxとy座標を代入してbを求めてみよう
それでいいね!
>>あゆたそ さん
求め方ありますよー!
合計人数が偶数の時:x÷2とx÷2+1の平均
合計人数が奇数の時:(x+1)÷2
です!
関数の問題である正方形があり、その正方形の面積を2分割する式の切片を求めよという問題があったのですが解答には正方形は点対称な図形だから対角線の交点を通る直線をかけと書いていたのですが、対角線の交点ではなく、片方の対角線で考えたらダメなのでしょうか?それで考えたら間違えてしまいました。
>関数の問題である正方形があり、その正方形の面積を2分割する式の切片を求めよという問題があったのですが解答には正方形は点対称な図形だから対角線の交点を通る直線をかけと書いていたのですが、対角線の交点ではなく、片方の対角線で考えたらダメなのでしょうか?それで考えたら間違えてしまいました。
確かに、対角線を引くと正方形の面積は二等分されるね。
ただ、それは正方形の頂点を2つ通るという条件でしか使えないね。
その点、対角線の交点を通る直線ならば、正方形の外側のどの向きから直線を引いても二等分される
方程式の文章問題で等式を立てれません
どうすればいいですか?
教えてください
空間の図形で含まれると交わるの違いを教えてください!
>方程式の文章問題で等式を立てれません
どうすればいいですか?
教えてください
とりあえず、いったん、問題で求めたいものを文字でおくといいよ
>空間の図形で含まれると交わるの違いを教えてください!
含まれてるとは、立体の平面の中の辺の1つになってるってことかな!
交わるとはこの平面にぐさっと全く違う角度からささってることだ
連立不等式
Ⅰx-3|>2
2x-3<9-4x
の解は
-5<x<2
で合ってますか?
中央値が25分となるようなxの値は全部で何個あるか。という問題です。
表は0~10が5、10~20がx、20~30が8、30~40が11、40~50がy、
50~60が2で、合計が35です。
ぜひ教えてください!お願いします
>中央値が25分となるようなxの値は全部で何個あるか。という問題です。
表は0~10が5、10~20がx、20~30が8、30~40が11、40~50がy、
50~60が2で、合計が35です。
まずは階級値を求めておこう。
今回は階級の数が偶数だから、中央値の求め方は(真ん中の2つの階級値の平均)になるね。
で、その平均が25になるってことは、2つの階級値を足したら50になる組み合わせを考えればいいね。
ある地域の貯金額の問題が分かりません。
その地域の人口は1000人。うち670人の貯金額が200万円、残り330人の貯金額が1000万円。その中央値の求め方を教えてください。
≫れいさん…!
気づくの遅くてすみません
ありがとうございます!(*゚∀゚*)
>その地域の人口は1000人。うち670人の貯金額が200万円、残り330人の貯金額が1000万円。その中央値の求め方を教えてください。
データ数が偶数の時は、真ん中の2つの数の平均をとって中央値にするよ。
データを大きい順番に並べると、ちょうど真ん中に当たる500と501番目の貯蓄額は200万円になりそうだね。
この2つのデータの平均をとってやればいいわけね
度数分布表がある場合で(分かりにくくて申し訳ないですが)、度数が大きい順に2、3、4、4、7と真ん中の数が同じ場合どちらの度数の階級で中央値を求めればいいですか?
※ 4の階級は30〜35(kg)と40〜45(kg)です。
相似の証明が難しいです。簡単な証明ならいいのですが、90度から角度を引いて考える問題や、相似比で比率を求めてから証明する問題などなど。
訳がわかりません。証明なんてしなくとも、見た感じで分かるやろ!と一人虚しく叫んでます。
証明がパッと解ける方法はありますか?
>度数分布表がある場合で(分かりにくくて申し訳ないですが)、度数が大きい順に2、3、4、4、7と真ん中の数が同じ場合どちらの度数の階級で中央値を求めればいいですか?
※ 4の階級は30〜35(kg)と40〜45(kg)です。
たしかにこのケースはどうするんだろう汗
4の階級値の平均をとってあげるんでいいんじゃなかろうか
>相似の証明が難しいです。簡単な証明ならいいのですが、90度から角度を引いて考える問題や、相似比で比率を求めてから証明する問題などなど。
訳がわかりません。証明なんてしなくとも、見た感じで分かるやろ!と一人虚しく叫んでます。
90度からひくやつむずいよね笑
相似の証明は、相似条件をしっかり覚えて、なんとかそいつらを満たすような根拠をくまなく探して行くほかはないね。
経験上、相似の証明は大体「2つの角が等しい」だからまずはそこから探してみるようにすればいいかな
混乱するー!
数字の大きい(小さい)順に簡単に並べるコツを教えてください‼お願いします‼
>数字の大きい(小さい)順に簡単に並べるコツを教えてください‼お願いします‼
ミスがないように並べた後に確認することかな!
中央値を求める際、0って含めるんですか?
大きい順に並べて、真ん中の値が中央値になるよ!
だから1つのデータが0になっていたらふくまるというか他のデータと同じように扱うよ
有効数字の求めかたを教えたください
後、有効数字の表し方も教えて下さい
有効数字の考え方を読んでみて
方程式の文章題だね。
問題で求めたいものを文字で置いてみよう。
この場合でいうと、「妹にお金を渡す前の姉の金額」だね。
あとは、「姉が妹に350円渡したところ、姉の持っている金額は妹が持っている金額の1.5倍になった」を等式にすればオッケー
X-350=(2000-X)×1.5
X-350=3000-1.5X
X+1.5X=3000+350
2.5X=3350
X=3350/2.5
X=1340 でよろしいのでしょうか?
2乗に比例する関数y=ax二条においてxの変域が-1以上x6以下の時yの変域は
0以上y12以下であるaのの値を求めなさい
の問題がわかりません解説お願いします
ある中学校の生徒8人について、10点満点のテストを行ったところ、
下のような結果になった。この8人の平均値と中央値が一致するとき
aの値を求めなさい。
ただし、aは整数とする。
3、5、1、7、8、1、2、a
この問題はどうやってとけば良いでしょうか?
たくさんの数が並んでいてその中央値を求めるとき、かぶっている数は数字一個と数えるんですか?
例えば・・・
76,32,73,73,91,21,42と並んでいるとき73は2こ書くのか
教えて下さい!
だるくて何もわからん
教えて下さい!
1800m離れた学校に向かって兄は7時にあるいて弟は7時十分に自転車に乗ってそれぞれ家を出ました。
弟は途中で兄を追いこし兄より十五分先に学校につきました。弟が兄を追いこしたのは家から何mのところですか?
この質問の答えをください!
わかりやすい。ありがとうございます。