【中3数学】因数分解とはなんだろう？？

因数分解とはなにものなの？？

こんにちは！この記事をかいているKenだよ。魚は2匹までだね。

中3数学では、

因数分解

をならうよ。

じつはこれ、けっこう重要な単元なんだ。

因数分解の問題がよくでることはもちろん、

二次方程式をとくためにも必要だからね。

もう、ぶっちゃけ、

因数分解を制するものは中3数学を制する

といっても過言じゃない。

そこで今日は手始めとして、

因数分解とはなにものなのか？？

を解説していくよ。

よかったら参考にしてみて^^

3分でわかる！因数分解とは何か？？

因数分解とはずばり、

「数」や「文字式」をあえて「かけ算」になおすこと

だ。

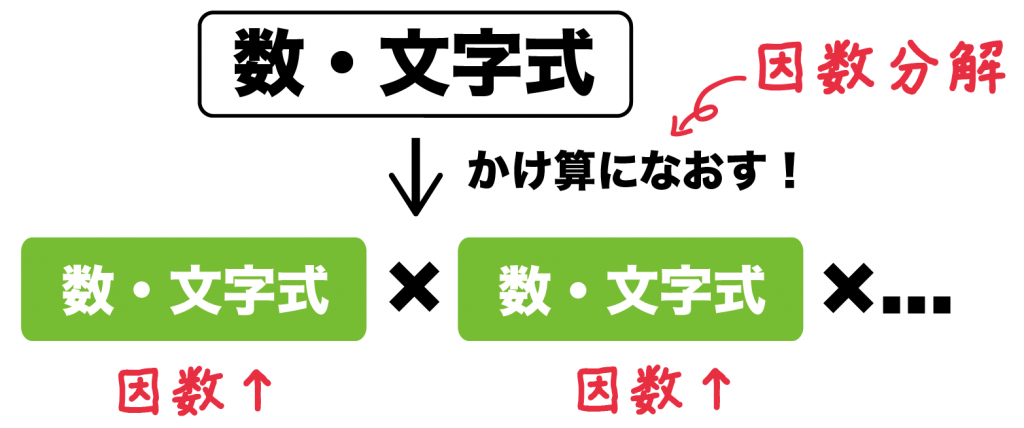
このとき、

かけられている数字・文字式を「因数」っていうんだ。

えっ？？

ぜんぜんピンとこないって？？

それじゃあ因数分解の例をみていこう！

因数分解の例1 .  自然数「35」

自然数の「35」をイメージしてみて。

因数分解とは、

あえて「かけ算」になおすこと

だったよね？？

「ごしちさんじゅうご」だから、35を因数分解すると、

5× 7

になる。

こんな感じで、

「35」を「5×7」になおすことを「因数分解」っていうんだ。

かけられている数を「因数」といったね？？

だから35の因数は、

• 5
• 7

の2つになるのさ。

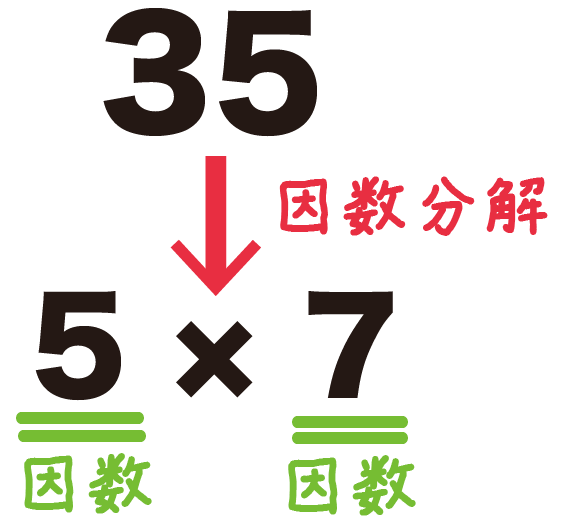
これが数字の因数分解の例だよ。

因数分解の例2.  文字式の場合

つぎは文字式の因数分解だ。

とりあえず、

a^2 -a

をイメージしてみて。

こいつをかけ算になおしてやろう。

aで（）でくくってやると、

a^2 -a
= a×(a-1)

になるよね。

「a^2 -a 」を「a × (a-1)」になおすことを「因数分解」っていうんだ。

そして、

「かけられているやつら」は「因数」だったよね？？

だから因数は、

• a
• a-1

の2つになるよ。

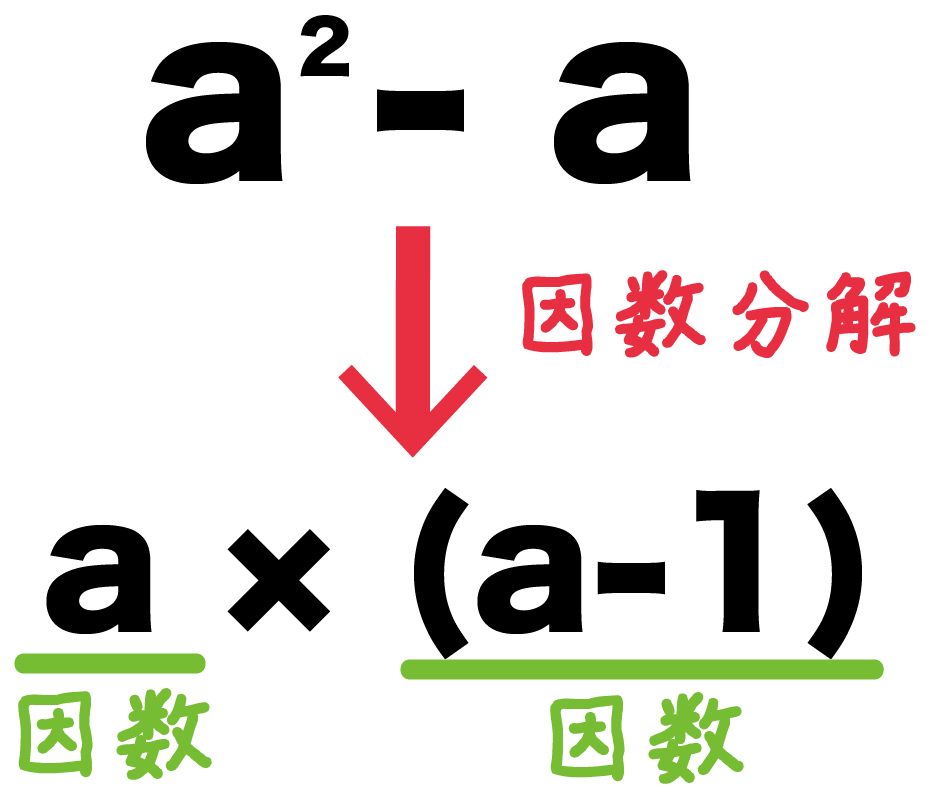
どう？？

納得したかな？？

因数分解とはぶっちゃけ「展開の逆」？？

ここまで因数分解とは、

数や文字式をあえて「かけ算」になおすこと

っていってきたね。

だけど、これじゃあよくわからない。

もっと簡単な覚え方ないかな？？

じつはもっとシンプルな方法があるんだ。

それは、

因数分解とは「展開の逆」

という覚え方。

展開とは、

かけ算を足し算の形になおすこと

だったよね。

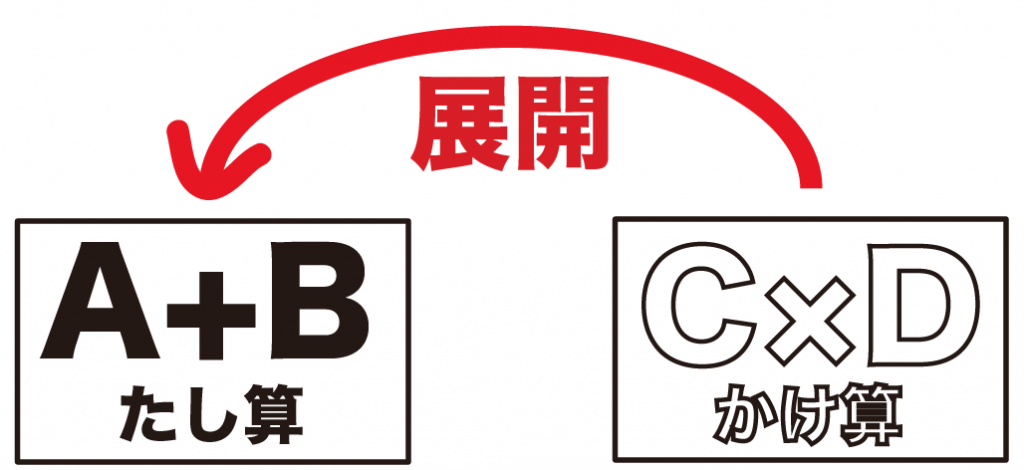
（）をはずしたり、展開の公式で計算したりしたやつだよ。

ずばり、

因数分解とは「展開とは逆のこと」をするんだ。

たとえば、「a^2 -a 」と「a(a-1)」の関係をみてみよう。

「a^2 -a 」を因数分解すると「a(a-1)」になったね？？

今度は逆に、

「a(a-1)」を分配法則で展開すると、

a(a-1)
= a^2 -a

になるね。

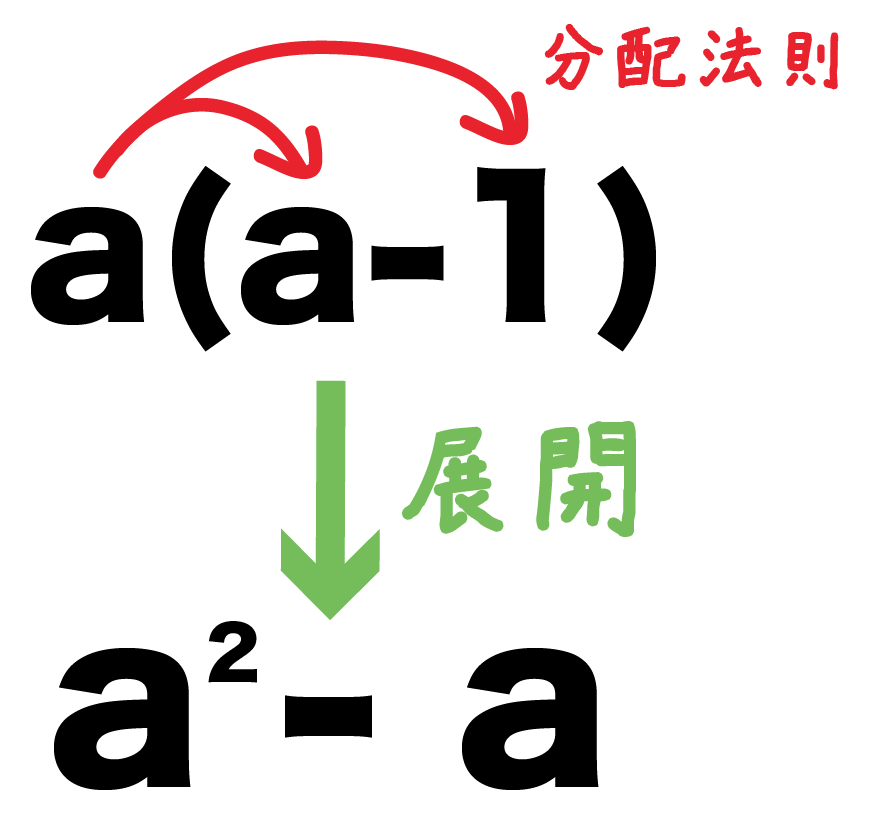
あら。

因数分解する前の「a^2 -a 」に戻っちゃったね。

これからわかるのは、

因数分解すると展開前の式になるし、

展開すると因数分解前の式にもどる

ってことさ。

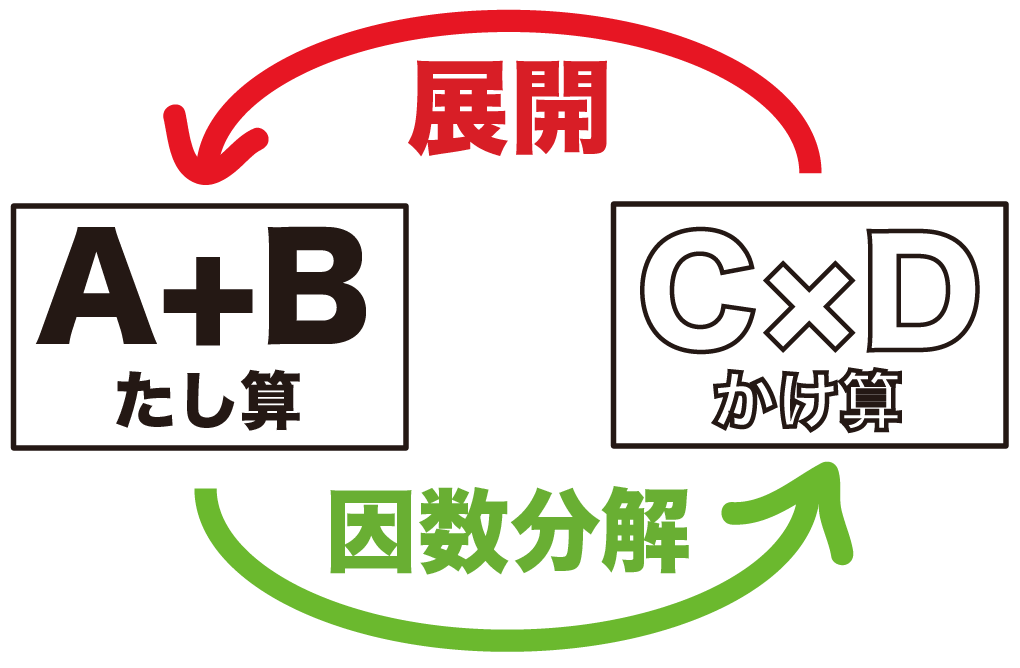
つまり、

因数分解とは「展開の逆」をしているんだね^^

まとめ：因数分解とは「展開の逆」！！

因数分解とは、

展開の逆。

これがいちばん覚えやすいかも。

因数分解する前によーく復習しておこう。

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。