中1数学にでてくる1次方程式(xの方程式)の解き方
こんにちは!イボコロリを使ってみたKenだよ。
中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「1次方程式」とよばれているものだ。なにせ、文字が1つしか含まれていないからね。
ちまたでは「xの方程式」と呼ばれているらしい^^

今日は「一次方程式」の解き方の手順を3つにわけて紹介するね。
でも、中1で勉強する1次方程式にも「むずかしいもの」と「簡単なもの」があるんだ。
まず手始めということで、
今日はxの方程式の解き方の基礎的な手順を書いてみた。よかったら参考にしてみてね^^
【基礎編】一次方程式の解き方の3つの手順
それでは簡単な1次方程式(xの方程式)の解き方を振り返ってみよう。xの方程式の具体例として、
7x-2 = 5x +10
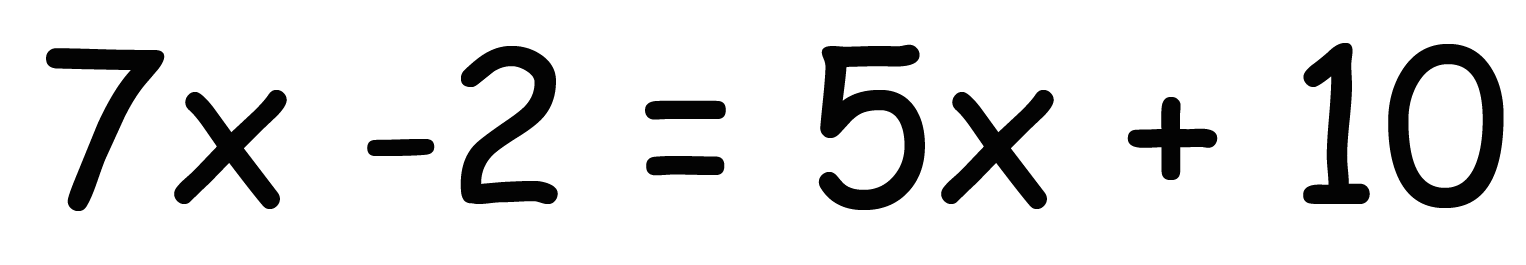
という方程式をつかって考えてみるね。
解き方1. 「x」を左によせろ!!
まず一次方程式(xの方程式)でやるべきことは、
等式の左に文字xの項をよせること
だ。この方程式でいえば、
「7x」と「5x」が「xの項」だよね?? だって、項の中にxが含まれているからね。
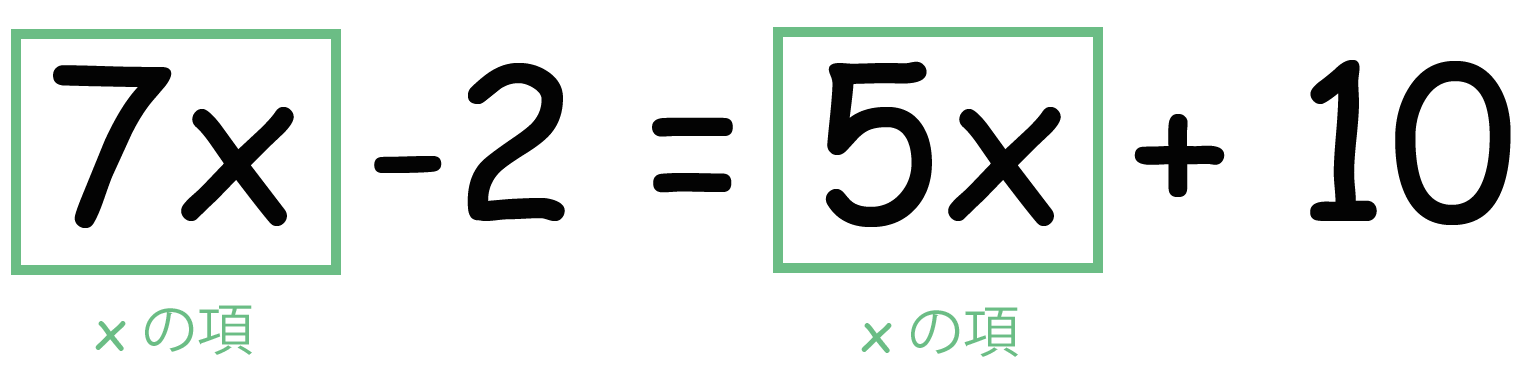
7xはもともと左にあるから、5xをがんばって左側に持ってこよう。
項を移動させるときは前回ならった「移項」というワザを使うんだ。超シンプルにいうと、移項とは「逆側に項を移すときに符号を変える」というもの。
だから、5xにマイナスの符号をつけて、コイツを左に持ってくるんだ。
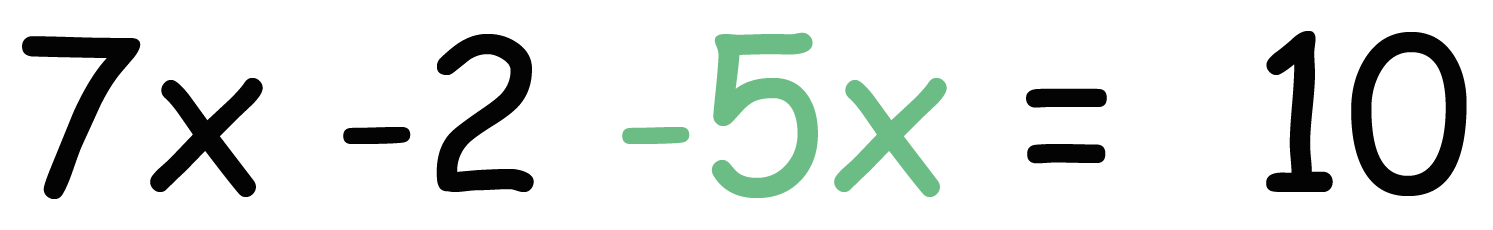
これで方程式の解き方の第一ステップは終了!
解き方2. 「数字」を右によせろ!!
次はx以外の項。つまり、数字の項を右側によせちゃおう!!
さっきの例でいえば、「-2」と「10」が数字の項だね。
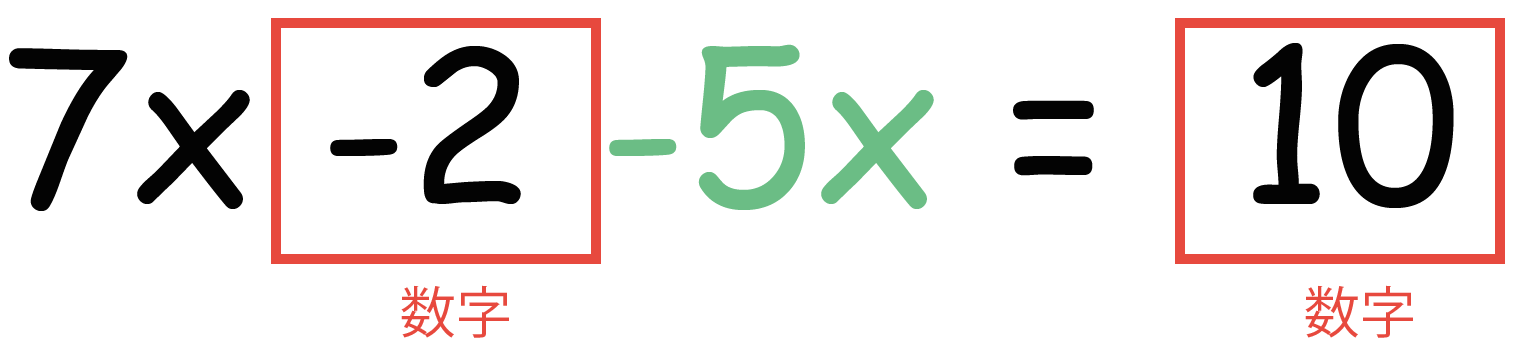
右への寄せ方は手順1と同じだよ。
そう。移項というワザを使ってやるんだ。符号を変えながら数字の「-2」という項を右へ移してやるとこうなる!
解き方3. 左と右でそれぞれ計算しちゃう
左に文字、右に数字を寄せたね??
次はその寄せた項同士で計算してもっとシンプルな形に変えてやればいんだ。足し算や引き算であることが多い。
さっきの例の「左」と「右」の計算をしてカンタンな式にしてやればこうなる↓↓
2x = 12
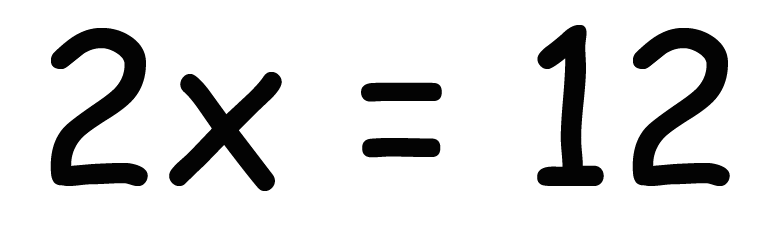
これは俗にいう、
ax = b のカタチ
というやつさ。ここまでくれば方程式は解けたも同然。あと一歩だから踏ん張ってみよう!!
解き方4. xを裸にしてあげる
最後はxを裸にしてあげるんだ。つまり、
x = ~~~~
というように、xの項の係数をかならず1にしてあげる。これを巷では「xを裸にする」といわれているんだ。
「解き方3」から「解き方4」に移行するためには、
xの係数で左と右の式を割ってあげればいい。
たとえばさっきの例でいえば、
左のxの項の係数は2だよね。だって、xの前に2がついているから。
だから左と右の両辺を「2」で割ってみよう。するとこうなって、

最終的にこうなる↓↓

つまり、
この方程式の解は「6」ということだね! xの値が方程式の解だから当然だよね?? これで中学1年生で勉強する「一次方程式」をマスターしたも同然だ。
一次方程式(xの方程式)の解き方、ゲットだぜ??
以上で一次方程式の解き方は終了だよ。
あくまでもこれは超基礎的な方程式の解き方。だからこれだけじゃ解けない方程式もあるよ^^
だから次回は、中1数学の方程式の解き方の応用編について語っていくよ。お楽しみにー!!
そんじゃねー!!
Ken
動画もみてね↓↓

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。





























3x+5(x+1)
まずは分配法則でかっこはずしてみよう!
2-x=1
2を右に移項してみよう!
(12x-16)➗4のやり方を教えてください
分配法則を使ってみよう!
分数と少数が混ざった計算が分からないです。
分数の計算が分かりません。方程式の!
小数を分数になおして、分数の方程式にしちゃおう
分母を払って、分数をなくせばいいのさ!
詳しくは「分数をふくむ方程式の解き方」を読んでみて!
絶対値の問題で
-0.44,2分の3,2.5,-3分の8,-2分の5,3
の中で絶対値が2以上3未満であるものはどれか。
という問題何ですが、よく分からないので解説
お願いします。
分数を小数に直すといいね!
絶対値だから、あとは符号抜きで2以上3未満になってるやつを選べばよし
2(A-3B)
A=x-2y
B=3x+4y-1の解き方
まずは2(A-3B)のかっこを分配法則で外してみよう!
3x+2a=5の解が3のとき、aの値を求めよ
この方程式はxに関する方程式だから、解が3ってことはxが3ってこと!
x = 3を代入してaに関する方程式を作って解いてみよう
3x+(1-4x)=
同じ文字を持つxの項をまとめてみよう!
3xと-4xだね。数字の1は放置
2分の3X-1=3分のX+1
0.5X-0.3=4.2
7x-2x=5x+10
29=8-3xのようにxが右にあるときは左に移項しますか?
分母を払おう!
2と3の最小公倍数を両辺にかけてみて!
小数を消し去ろう。
両辺を10倍してみて!
まずはxの項を左に集めよう。
5xを左に移してみて!
移行しなくても大丈夫だよ!間違えなければ!
3x-4=-1
数字の項を右に寄せてみよう!
-4を右辺に移行してみて!
= がない場合たとえば「−8a+7-9a-5」です。 教えてください
(6x+4)-(-x-2)
わからない 助けてー
>= がない場合たとえば「−8a+7-9a-5」です。 教えてください
同類項をまとめる問題だね。
文字は文字、整数は整数で計算してみよう
>(6x+4)-(-x-2)
分配法則で()を外してみよう。
-(-x-2)は-1×(-x-2)と一緒!
次の方程式を解け
x:(x+1)=1:1
とありますが xが消えてしまい解けません
助けてください!
消えるね笑
そもそもxとx+1が等しいってことを言ってるから、これはありえないね!
a町からb町までの道のりは21kmです。a町を出発してb町に向かった人が、はじめは平地を時速5kmで歩き、次に、のぼり坂を時速3kmで歩いて、全体で8時間かかりました。平地、のぼり坂の道のりをそれぞれ求めなさい。という問題がわかりません
方程式を言い換えると?
まずは問題で求めたいものを文字で置いてみよう。
あとは、時間に関する等式を作ればオッケー
何が入るかわからない文字が入った等式かな
3x=2xー6
>3x=2xー6
2xを左に移項して、同類項をまとめてみて
ある数を2倍にして5でわると、商が7、余りが3になった。ある数を求めよ。
という問題の解き方を教えてください。
200×100/5+×=(200+x)×100/24の仕方がわかりません教えて下さい
>ある数を2倍にして5でわると、商が7、余りが3になった。ある数を求めよ。
ある数をxとしてみよう。
2倍して5で割ったら、7とあまりが3になるっていう等式を作ればオッケー
>200×100/5+×=(200+x)×100/24
分母の100を両辺にかけて分数を消し去ろう!
方程式の定義とは?
5x+7(12-x)=1500
>方程式の定義とは?
わからない文字が含まれる等式かな
−21=35−4x
>5x+7(12-x)=1500
まずは分配法則で()を外してみよう。
次にxの同類項をまとめて、数字を右に移項していこうぜ
>−21=35−4x
35を左辺に移項して整数同士の計算してみよう
30x=-5のやり方を教えて下さい!
4(x-3)=6-(3-x)の解答
10(11ーx)+x=10x+(11−x)+45
>30x=-5
xの前についている係数(30)で両辺を割ってみよう。
すると、x=の形になるはずだ
>4(x-3)=6-(3-x)
分配法則で()を外してあげよう。
次は移項でxの項を左辺に、それ以外を右辺に移動してみて
>10(11ーx)+x=10x+(11−x)+45
分配法則で()を外してみよう。
あとは移項して左辺にxの項、右辺に数字の項を持ってこよう。
この問題わかりますか?
ある中学校の昨年の生徒数は、男女あわせて685人であった。
今年の生徒数は、男子が12%増え、女子が10%減って、全体では三人増えた。
今年の男子と女子の人数を、それぞれ求めなさい。
これをできれば月曜日(9月4日)までにお願いします。
>ある中学校の昨年の生徒数は、男女あわせて685人であった。
今年の生徒数は、男子が12%増え、女子が10%減って、全体では三人増えた。
今年の男子と女子の人数を、それぞれ求めなさい。
この問題はあえて昨年の人数を文字でおいた方が計算しやすいね。
ってことで、昨年の男子の人数をx人と置いてみよう。
あとは、今年の男女の人数に関する等式を作ればオッケー
方程式2X-3分のX+a=a+3の解が-2であるとき、定数aの値を求めよ。
↑↑
この問題教えてください!
400÷1000+(x)÷1000=1
>方程式2X-3分のX+a=a+3の解が-2であるとき、定数aの値を求めよ
解が-2ってことはxが-2ってこと。
x=-2を代入してaの方程式を作ってあげよう
>400÷1000+(x)÷1000=1
分母を払ってみよう。
両辺に1000をかけると、割り算の部分がスッキリして解きやすくなるよ
0.2X-3=-1.3X+6
>0.2X-3=-1.3X+6
両辺を10倍して小数を消そう。
詳しくは「小数を含む方程式の解き方」を読んでみて
8x=24
一次方程式の文書題です
ある中学校の一年生の生徒数は男子は女子より10人少ない。男子の30%と女子の15%は塾通いしておりその合計はその22%にあたる。この中学校の一年生の人数は全部で何人か。
>8x=24
両辺をxの前についている係数の8で割ってみよう。
>ある中学校の一年生の生徒数は男子は女子より10人少ない。
男子の30%と女子の15%は塾通いしておりその合計はその22%にあたる。この中学校の一年生の人数は全部で何人か。
女子の人数をx人としてみよう。
あとは男子の人数をxで表して、塾通いの人数に関する方程式を立てればいいね
一次方程式を使うことの利点は何ですか?
>一次方程式を使うことの利点は何ですか?
求めたい数値がわかることかなー
-x=2x+2
>-x=2x+2
2xを左に移行してみよう!
グラフの、y=axに直すのに、2x+6=yの場合はどうしたらいいですか?
>グラフの、y=axに直すのに、2x+6=yの場合はどうしたらいいですか?
これは左右の項を入れ替えて、
y=2x+6
でいいんじゃないかな。xの前の2がaで、そのほかの6が切片だ
方程式が思い出せない人
6000X+4000Y=196000
X+Y =40
これが解けないです。
>6000X+4000Y=196000
X+Y =40
1つ目の式の係数が大きいね。
一旦、0が3つ全部の項についてるから、両辺を1000で割ればもっと簡単になるはず。
Y-(2-y)=2+4y
>Y-(2-y)=2+4y
()を分配法則で外して移項して、
同類項をまとめてyの値を出そう
52円切手と82円切手を合わせて10枚買ったところ、代金の合計が700円になりました。それぞれの切手を何枚買いましたか?代金の関係から方程式で求めなさい。
>52円切手と82円切手を合わせて10枚買ったところ、代金の合計が700円になりました。
それぞれの切手を何枚買いましたか?代金の関係から方程式で求めなさい。
52円切手をx枚買ったとして、82円切手を買った枚数をxで表してみよう
容器Aに10%の食塩水が300g、容器Bに4%の食塩水が600g入っている。A、BそれぞれからXgずつ取り出し、入れかえたとき、同じ濃度になったという。この時の食塩水の濃度を求めなさい。また、Xの値を求めなさい。
>容器Aに10%の食塩水が300g、容器Bに4%の食塩水が600g入っている。A、BそれぞれからXgずつ取り出し、入れかえたとき、同じ濃度になったという。
この時の食塩水の濃度を求めなさい。また、Xの値を求めなさい。
入れ替えた後の濃度をY%としてみよう。
あとは、入れ替えた後に食塩の重さを合計したら、入れ替える前の食塩の重さになるっていう等式を作ればオッケー
5(X-4)=3X
>5(X-4)=3X
()を分配法則で展開して、
xの項を左辺に、それ以外を右辺に移項してみよう
現在Aの年齢はBの年齢の三倍であるが、15年後にはAの年齢がBの年齢の二倍になると言う。現在のAの年齢とBの年齢を求めなさい。
この問題がわからないので、教えて欲しいです。。。
>現在Aの年齢はBの年齢の三倍であるが、15年後にはAの年齢がBの年齢の二倍になると言う。現在のAの年齢とBの年齢を求めなさい。
この問題がわからないので、教えて欲しいです。。。
方程式の文章題では、求めたいものを文字でおけばいいね。
ってことで、現在のAの年齢をx歳と置いて、Bの年齢をxで表してみて。
あとは「15年後にはAの年齢がBの年齢の二倍になる」を等式にすればオッケー
かっこがついた方程式の解き方がよく分かりません
>かっこがついた方程式の解き方がよく分かりません
()を展開してみよう。
おそらく分配法則を使うんじゃないかな
50人の生徒の中で眼鏡をかけている人数は、男子の10分の3と女子の4分の1であり、その人数の合計は、全体の人数の25分の7に当たる。男子生徒の人数を答えなさい。
解き方を教えてください。。
>50人の生徒の中で眼鏡をかけている人数は、男子の10分の3と女子の4分の1であり、その人数の合計は、全体の人数の25分の7に当たる。
男子生徒の人数を答えなさい。
男子生徒の数をx人としよう。
あとは、女子の人数をxで表して、
「男子の10分の3と女子の4分の1であり、その人数の合計は、全体の人数の25分の7に当たる」を等式にすればオッケー
一次
方程式のやり方がさっぱり分かりません。
すごく簡単な方法があれば教えてくださいおねがいします。
>一次方程式のやり方がさっぱり分かりません。
すごく簡単な方法があれば教えてくださいおねがいします。
一次方程式を理解するために必要なのは、
等式の性質だ。
簡単にいうと、左辺と右辺に同じ数を足したり、引いたり、かけたり、割ったりしても等式が保たれるってやつだ。
だから、移項もできるし、xの前の係数で両辺を割っても平気なんだね。
ここがわかれば方程式が解けるようになるよ
-4 x=11
の解き方を教えて下さい。
>-4 x=11
両辺をxの係数-4で割ってみよう!
(14400+X)×0.6=17900
>(14400+X)×0.6=17900
両辺を10倍して小数を消し去ろう!
詳しくは「小数を含む方程式の解き方」を読んでみて
x-1=3分の5-1
>x-1=3分の5-1
左辺の-1を右辺に移項してみようぜ!
x+10=2(x+3)-1を教えて下さい。
>x+10=2(x+3)-1
()を分配法則で展開してみよう!
あとはxの項を左に移項してそれ以外を右へ
4(3a+1)ー(7aー5)の解き方を詳しくおしえてください!
>4(3a+1)ー(7aー5)
分配法則で()を外してみよう!
あとは同類項をまとめるだけ
5x=-13の場合xどうやって消すんですか?
一本百円の鉛筆と一本百三十円のボールペン
を合わせて八本買ったら、代金の合計は、百六十円だった。鉛筆x本にして答えなさい。
この問題の場合はどう計算しますか?
>5x=-13の場合xどうやって消すんですか?
両辺をxの前についている係数5で割ればいいよ
>一本百円の鉛筆と一本百三十円のボールペン
を合わせて八本買ったら、代金の合計は、百六十円だった。鉛筆x本にして答えなさい。
ボールペンの本数をxで表してみよう。
これができたら、代金の合計に関する等式をつくればいいね
AとBの間は5000mあります。
C君はAからBまで一定の速さで歩き
DさんはC君が出発後16分後にBを出発し
同じルートをAまで分速220mの速さで
移動した。
Aから二人がすれ違った地点までのルートを求めなさい。
>AとBの間は5000mあります。
C君はAからBまで一定の速さで歩き
DさんはC君が出発後16分後にBを出発し
同じルートをAまで分速220mの速さで
移動した。
Aから二人がすれ違った地点までのルートを求めなさい。
逆方向からすれ違うってことは、2人が移動した距離をたすと
AB間の距離になるってことだ。
CとDの移動した距離の合計=AB間の距離
という等式を作ってみよう
4x(2X-10)x2分の1=6
教えてください
>4x(2X-10)x2分の1=6
両辺に分母の2をかけて分数を消し去ろう!
お恥ずかしい質問で恐縮なのですが
x + 0.4x = 672
↑ ここが
1.4x = 672
1.4x になるのがなぜかわかりません・・
そのあと
x = 672 /1.4
なぜ割り算なのかもわかりません・・
アドバイスをお願いいたします
10ぶんの3x-2ぶんの3=5ぶんの4x+1
の計算の仕方を教えてください!
>お恥ずかしい質問で恐縮なのですが
x + 0.4x = 672
↑ ここが
1.4x = 672
1.4x になるのがなぜかわかりません・・
そのあと
x = 672 /1.4
なぜ割り算なのかもわかりません・・
アドバイスをお願いいたします
x + 0.4x
は一旦文字なしで考えるとわかりやすいかも。
()でくくると、
x(1+0.4)
になるから、1+0.4を計算してxをくっつければいいわけだ。
>x = 672 /1.4
なぜxの前についている1.4で割っているのかというと、
左辺をx=の形にして、
xの値を求めたいからだね。
等式では両辺を同じ数で割るのはありなのよ
−8x=8のときって
−x=1になるんですか?
どうしたらいいのか
よくわからなくて…
>10ぶんの3x-2ぶんの3=5ぶんの4x+1
分母の最小公倍数10を両辺にかけて分数を消し去ろう。
詳しくは「分数を含む方程式の解き方」を読んでみて
>−8x=8のときって
−x=1になるんですか?
なるね。
これは両辺を8で割るとそうなるね。
等式の性質には、
「両辺を同じ数で割っても等式が保たれる」
っていうやつがあるからそれを利用しているわけだ
3x-5=7
ってどうやって計算しますか?
>3x-5=7
xがつく項を左に、それ以外を右に移項してみよう。
あとは最後にxの係数で割ってやればいいね!
3分の1x+2=6−xで解が−6であるかどうか
1.3(2x-5)=0.9x+2
ってどうやって計算したらいいでしょうか
>3分の1x+2=6−xで解が−6であるかどうか
x=-6を代入して等式が成り立つか調べてみよう!
>1.3(2x-5)=0.9x+2
両辺を10倍して小数を消し去ろう。
詳しくは「小数を含む方程式の解き方」を読んでみて
5x-9=(x-5)X9の解き方がわかりません
正方形の厚紙の4すみから1辺が2cmの正方形を切り取り、深さ2cm、容積128cm3の箱を作る元の正方形の形の長さを何cmにすれば良いか求めなさい。
この問題どうやって解けばいいですか?
>正方形の厚紙の4すみから1辺が2cmの正方形を切り取り、
深さ2cm、容積128cm3の箱を作る元の正方形の形の長さを何cmにすれば良いか求めなさい。
深さはわかってるから、あとは縦・横の長さがわかればいいね。
こいつらの長さをxで表してみよう。
正方形の厚紙の4すみから1辺が2cmの正方形を切り取り、深さ2cm、容積128cm3の箱を作る元の正方形の形の長さを何cmにすれば良いか求めなさい。
この問題どうやって解けばいいですか?
>正方形の厚紙の4すみから1辺が2cmの正方形を切り取り、深さ2cm、容積128cm3の箱を作る元の正方形の形の長さを何cmにすれば良いか求めなさい。
一辺の長さをxcmとして、切り抜いたときの体積をxで表してみよう。
ポイントは、正方形からできる直方体のたてと横の長さをxで表せるかだね
50円のはがきと80円切手を合わせて20枚買ったところ、代金の合計は1270円であった。買ったはがきと切手の枚数をそれぞれ求めなさい。
はどうするんですか?
1.2:2.1=8:x
>50円のはがきと80円切手を合わせて20枚買ったところ、代金の合計は1270円であった。買ったはがきと切手の枚数をそれぞれ求めなさい。
ハガキの枚数をx枚としてみよう。
切手の枚数をxで表して、
あとは代金の合計に関する等式を求めてみよう
>1.2:2.1=8:x
内向の積 外向の積で解いてみよう!
詳しくは「比例式の解き方」を読んでみて
Aさんは、サイクリングで、地点P、Q間を行きは時速12km、帰りは時速18kmで、往復したら5時間かかりました。往復にかかった時間が、5時間であることから、方程式を作りなさい。っていう問題の解き方を教えてください。
>Aさんは、サイクリングで、地点P、Q間を行きは時速12km、帰りは時速18kmで、往復したら5時間かかりました。
往復にかかった時間が、5時間であることから、方程式を作りなさい
PQ間の距離をxkmとして方程式を作ってみよう。
道のり÷速さ
で行き帰りにかかった時間を算出し、足したら5時間になるという等式を作ればオッケー
a=-3,b=7のとき2a+3bの値
>a=-3,b=7のとき2a+3bの値
aとbを2a+3bに代入してみよう!
数学
x+3=12
説明詳しくお願いします!
>x+3=12
xじゃない項を右に移項しよう。この場合+3だね
1000-(3x+280)=60
>1000-(3x+280)=60
分配法則で()を外してみよう。
あとはxの項を左辺、それ以外を右辺に移行すればいいよ
X÷(100+x)×100=20 x=25らしいのですが、なぜこうなるのですか? 計算方法を教えてください(^_^;)
>X÷(100+x)×100=20
100+xを両辺にかけて分数を消し去ろう。
0.015x=2+(100-x)÷10
X=104.347…
なぜこうなるのかわかりません(;_;)
>0.015x=2+(100-x)÷10
小数を含む方程式だね。
両辺を1000倍して小数を消し去ろうぜ
3x-2{x-(1-2x/3)}=(2x-1/2)
>3x-2{x-(1-2x/3)}=(2x-1/2)
一番()の内側から計算していこうぜ
4x-5=x-6
2x+5=3x+1が解けません
>4x-5=x-6
xを左辺に、数字を右辺に移項してみよう
>2x+5=3x+1が解けません
こいつも同じだね!
2x-3=x+1
>2x-3=x+1
xを左辺に、それ以外を右辺に移項してみようぜ
2直線y=2x-3,y=-½+ニブンノゴa
がy軸上で交わる時定数aの値を求めなさい
1時間数の問題です!教えてください
2直線 y=2x-3,y=-½x+ニブンノゴa
がy軸上で交わる時定数aの値を求めなさい。
が分かりません!教えてください
>2直線y=2x-3,y=-½+ニブンノゴa
がy軸上で交わる時定数aの値を求めなさい
1時間数の問題です!教えてください
y軸上で交わるってことは切片が等しいってことだね!
このヒントからaに関する方程式を作ってみようぜ
下の表は牛肉、牛乳それぞれ100gに含まれるタンパク質と脂肪の量を示したものであるこれらから、タンパク質を30g、脂肪を25g取るには牛肉、牛乳をそれぞれ何g取ればいいか求めなさい。
タンパク質 脂肪
牛肉 18g 8g
牛乳 3g 3g
がわかりません……教えてください!
>下の表は牛肉、牛乳それぞれ100gに含まれるタンパク質と脂肪の量を示したものであるこれらから、タンパク質を30g、脂肪を25g取るには牛肉、牛乳をそれぞれ何g取ればいいか求めなさい。
タンパク質 脂肪
牛肉 18g 8g
牛乳 3g 3g
がわかりません……教えてください!
牛肉をxg、牛乳をyg取るとして、タンパク質の式、脂肪の式を作ってみようぜ!
2x−6=0
どうやって解くんですか??
>2x−6=0
どうやって解くんですか?
-6を右に移項して両辺をxの係数で割ってみよう
5(x-1)(x+2)(x-3)=0
の解き方を教えてください。かっことかっこはくっついています。
>5(x-1)(x+2)(x-3)=0
かけて0になるってことは、
(x-1)=0
(x+2)=0
(x-3)=0
のどれかになるはずだ!
x-1 3x-1
ー = ーーー
3 4
4(x-1)=3(3x-1)
4x-9x=-3+4
どうしても計算出来ないんですがどこが間違えていますか?
あってるよ〜
(x+24)÷5=15
x=51
なんで51になるんですか?
>(x+24)÷5=15
両辺に5をかけてみよう。
詳しくは「分数を含む一次方程式の解き方」を読んでみてね
こんにちは。
-6x+4=-6x-4
はどう計算すればいいのでしょうか?
-6X+6X=-4-4
0=-8になってしまうのですが(ならないはず・・・)
すごく分かり易かったです。
3x+5=11
>こんにちは。
-6x+4=-6x-4
はどう計算すればいいのでしょうか?
-6X+6X=-4-4
0=-8になってしまうのですが(ならないはず・・・)
これは等式として成り立ってないからどこか間違ってる!
数値をもう一度確認してみよう
>3x+5=11
5を右に移項してみようぜ
8x-1=9x-8
8x-9x=-8+1
-1x=-7
のあとの解き方を教えてください!
あと
-1x=-12 や -1x=-17 という場合どうすればいいんですか?
>8x-1=9x-8
8x-9x=-8+1
-1x=-7
のあとの解き方を教えてください!
最終的にx=の形に持っていけるようにすればいいね。
この形だと、両辺に-1をかけるとそうなるぜ!
少数どうしの方程式教えて下さい。
>少数どうしの方程式教えて下さい。
小数を含む方程式の解き方を読んでみて〜
-3x+1=-x+6
この問題だけ、何故か何度やっても解けません。
移項する時に間違っているのでしょうか…?
ぜひそこから教えて頂けると嬉しいです。
>-3x+1=-x+6
xを左辺に、それ以外を右辺に移項しよう。
-3x + x = 6 -1
となるね!
方程式の移行する意味はなんですか?
>方程式の移行する意味はなんですか?
移項することで、等式が成り立つ状態を保ったまま式を変型できるんだ
3(3x−7)=4(2x−1)って分配法則使わないで解けますか?教えてください。
>3(3x−7)=4(2x−1)
分配法則使おうぜ〜
3(2x+5)+1=-8のやり方がわかりません
>3(2x+5)+1=-8
まずは3(2x+5)を分配法則で展開。
あとはx以外の項を右に移項させて最後にxの係数で両辺を割ればいいね
0=2x−18
が解けません。
>0=2x−18
まずは18を左に移項して最後にxの係数2で両辺を割るといいよ。
こんな感じで、
xの項とx以外の項を分ける、
xの係数で両辺をわる
というステップを踏めば解けるはずだ
僕は数学が苦手です。 どうやったら数学が楽しく解けますか?
>僕は数学が苦手です。 どうやったら数学が楽しく解けますか?
まずは簡単な問題が解けるようになると楽しくなってくるよ。
基礎を固めてみようぜ
次のそれぞれの場合について、文字aの値を求めると言う問題の
方程式2xーa=5ーxの解がx=ー4と言う問題と
方程式3aー5x=aー3xの解がx=2と言う問題の途中式と答えをお願いします。
xを代入してaについての方程式を作ろう。
そしてそれを解けばaの値が求めれるはず
6x+2(x-3)
2(xー5)=3(2ーx)+4の途中式と答えをおねがいします。
すみません、ゆとり世代の先生がデタラメ教えて困っています。
40:25=×:15
この問題は、私の記憶では、xが左だと思うのですが、ゆとり世代の先生は、xを右側に教えます。
回答宜しくお願いします。現中2から詰めこみに戻ったので、ゆとり世代の先生が教えらろなくて困っています。
>6x+2(x-3)
まずは分配法則で後ろの()を外してやろう!
そしたら同類項をまとめればいいね
>2(xー5)=3(2ーx)+4
分配法則で()を展開してxの項を左、それ以外を右に移動しよう
>すみません、ゆとり世代の先生がデタラメ教えて困っています。
40:25=×:15
この問題は、私の記憶では、xが左だと思うのですが、ゆとり世代の先生は、xを右側に教えます。
回答宜しくお願いします。現中2から詰めこみに戻ったので、ゆとり世代の先生が教えらろなくて困っています。
たしかに左のほうが美しいけどぶっちゃけどっちでもいいと思います笑
解けりゃいい。(ちなみにぼくもゆとりです笑)
X={X+(X+2160)}× 5
100
(かける ひゃくぶんのご)
のやり方を教えてくれますか?
両辺に100をかけて分母を消し去ろうぜ!
x +(3分の2x +100)
これは方程式?
4分のX=-3はなんですか?
両辺に分母の数をかけてみよう
3分の4(x+4分の7)=2分の3-4分の1-xの解
両辺に12かけるといいな
7x-2(-x+4)=15x-2
教えて!
まずは-2(-x+4)を分配法則で()外してやろう。
その次に移項してみよう
3(3x-1)=4(X-2)
教えて欲しいです!
まずは分配法則で()外してみよう!
申し訳ありません・・・
基本的な一次方程式の問題なのですが、解き方をド忘れしてしまって・・・
以下、問題文です↓↓
【xについての方程式ax+12=3(3+a)x-aの解は2である。aの値を求めよ】
右辺の3(3+a)xを先に分配法則してからxの解を代入しようと考えているのですが、
①9+3ax ②(9+3a)x ③9+3a+x
この三つの考え方のどれが正しいのですか?教えてください・・・(スミマセン)
2だね!
5(x-2)-2(3x-4)=0
分配法則で()をはずすといいな!
9ー3x=2xー(x+7)
まずは()を分配法則ではずすといいな!
初めまして。5-8x=-3x+5が答えがx=0になってしまうのですがこれってあってますか?0になることってあるんでしょうか?
あるんじゃねえかな
-6X=3の解き方が分かりません。
xの係数-6で両辺を割ってみようぜ
x+6=3のような方程式が分かりません。解き方の解説と答えをください。なるべく早くお願いします。
移項をマスターすると解けるぞ!
6x=5-9xの解き方教えてください
xの項を左に持っていくといいな!
x+18=-3x+2
3x+2=x+7がどうしても分からないのですが、、、よかったらやり方を教えてください
40(20xー70)=50(10xー40)+1000
をわからないので教えていただけませんか?
(1.45x−800)−x=1000
解き方が分からないので教えて下さい。
方程式の文章題の片方を求めてもう片方を出すときの、どちらか一個見つけるやり方が
よく分かりません よかったら教えてください。
式が
4x−1 = 6xプラス1
ーーーー ーーーーーー
7 3
のときはどうしますか?